原文
1. 要約/背景
- 階層ベイズモデルをベースに、階層ディリクレモデルとDBMを組み合わせた学習器を開発した。
- 画像認識、人間の動きの検知に応用できる。
2. 骨子の理論
(1)DBM
3層積み上げた時のエネルギー関数は次のようになる。
E({\bf v}, {\bf h}; {\bf \psi}) = - \sum_{ij}W^{(1)}_{ij}v_ih^{(1)}_j - \sum_{jl}W^{(2)}_{jl}h^{(1)}_jh^{(2)}_l - \sum_{lk}W^{(3)}_{lk}h^{(2)}_lh^{(3)}_k
RBM同様、可視変数および隠れ変数は、エネルギー関数に基いたボルツマン分布に従う。
P({\bf v};{\bf \psi}) = \frac{1}{Z(\psi)}\sum_{{\bf h}}\exp(-E({\bf v}, {\bf h}^{(1)},{\bf h}^{(2)},{\bf h}^{(3)};\psi))
対数尤度の勾配は、次の式に従う。
\frac{\partial \log P({\bf v};\psi)}{\partial{\bf W}^{(1)}} = E_{P_{data}}\big[{\bf v} \, ^t{\bf h}^{(1)}\big] - E_{P_{model}}\big[{\bf v} \, ^t{\bf h}^{(1)}\big] \\
\frac{\partial \log P({\bf v};\psi)}{\partial{\bf W}^{(2)}} = E_{P_{data}}\big[{\bf h}^{(1)} \, ^t{\bf h}^{(2)}\big] - E_{P_{model}}\big[{\bf h}^{(1)} \, ^t{\bf h}^{(2)}\big] \\
\frac{\partial \log P({\bf v};\psi)}{\partial{\bf W}^{(3)}} = E_{P_{data}}\big[{\bf h}^{(2)} \, ^t{\bf h}^{(3)}\big] - E_{P_{model}}\big[{\bf h}^{(2)} \, ^t{\bf h}^{(3)}\big]
(2)分布の近似
任意の近似分布を$Q({\bf h}|{\bf v};{\bf \mu})$とする。
隠れ変数の最適な事後分布を、変分下限から次のように評価する。
\begin{align}
\log P({\bf v};\psi) &\geq \sum_{{\bf h}}Q({\bf h}|{\bf v};\mu)\log P({\bf v},{\bf h};\psi) + \mathcal{H}(Q) \\
& \geq \log P({\bf v};\psi) - {\rm KL}(Q({\bf h}|{\bf v};\mu)||P({\bf h}|{\bf v};\psi))
\end{align}
事後分布は平均場近似する。
Q^{MF}({\bf h}|{\bf v};\mu) = \prod_{j=1}^{F_1}\prod_{l=1}^{F_2}\prod_{k=1}^{F_3}q(h_j^{(1)}|{\bf v})q(h_l^{(2)}|{\bf v})q(h_k^{(3)}|{\bf v})
(3)MCMCによるサンプリング
(4)DBMの積層は、貪欲法により進行する。
一方で、最高層h3に対する事前分布は次のように表される;
P({\bf v},{\bf h}^{(1)},{\bf h}^{(2)}|{\bf h}^{(3)}) = \frac{1}{{\mathcal Z}(\psi, {\bf h}^{(3)})}\exp\big( \sum_{ij}W_{ij}^{(1)}v_ih_j^{(1)} + \\
\sum_{jl}W_{jl}^{(2)}h_j^{(1)}h_l^{(2)} + \sum_{lk}W_{lk}^{(3)}h_l^{(2)}h_k^{(3)} \big)
ここで最高層を「トピックモデル」で表現する。
「トピック→ドキュメント」「単語→トピック」の分布は、ディリクレ分布に従う。
{\bf \theta}_n | {\bf \pi} \sim {\rm Dir}(\alpha{\bf \pi}), {\rm for \: each \: document} \: n = 1, ..., N, \\
{\bf \phi}_t | {\bf \tau} \sim {\rm Dir}(\beta{\bf \tau}), {\rm for \: each \: topic} \: t = 1, ..., T, \\
x_{in} | {\bf \theta_n} \sim {\rm Mult}(1,{\bf \theta_n}), {\rm for \: each \: topic} \: i = 1, ..., M, \\
h_{in}^{(3)} | x_{in}, {\bf \phi}_{x_{in}} \sim {\rm Mult}(1,{\bf \phi}_{x_{in}})
3. モデル適用例
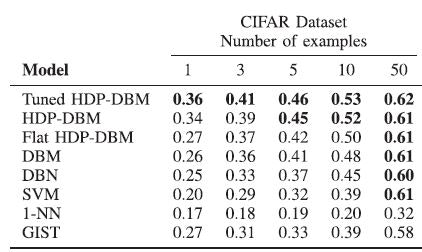
CIFARの画像データセットによるテストでは、最高のパフォーマンスを示した。
(数値は、Area Under the ROCで、数値が高いほど識別能力が高い。)