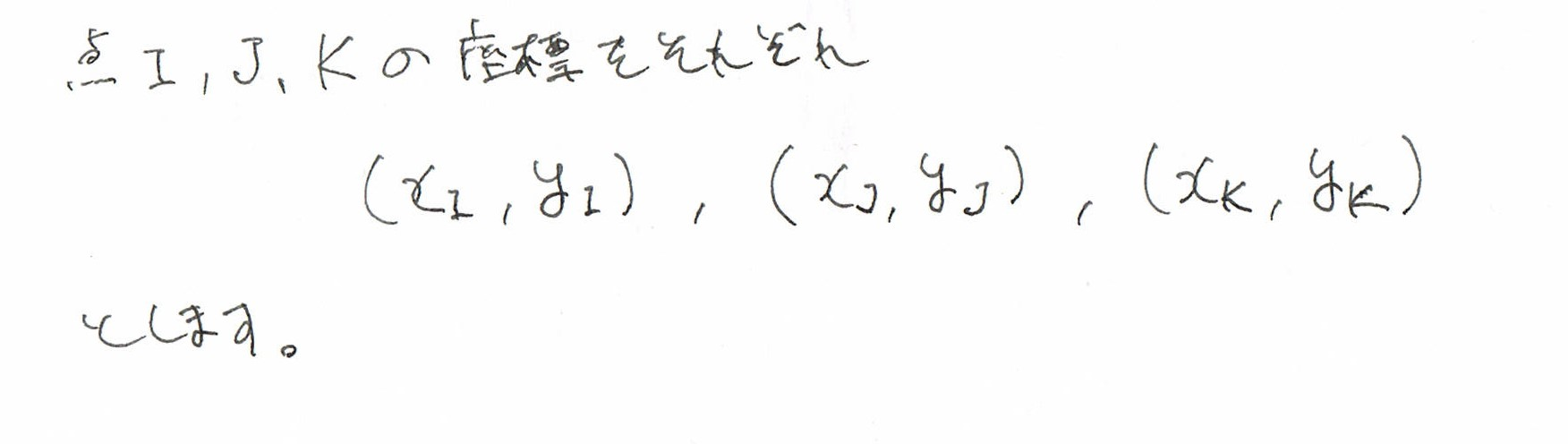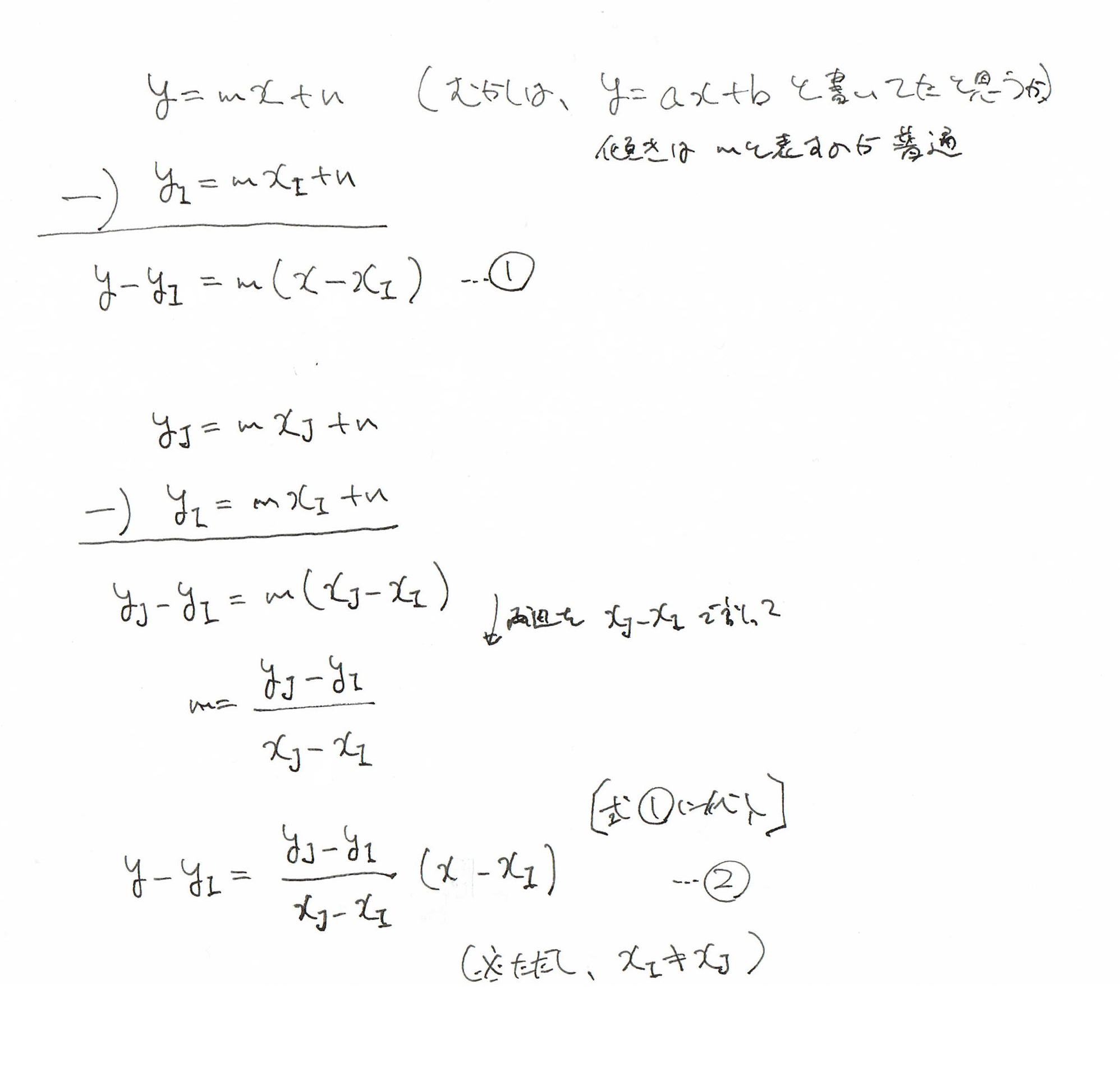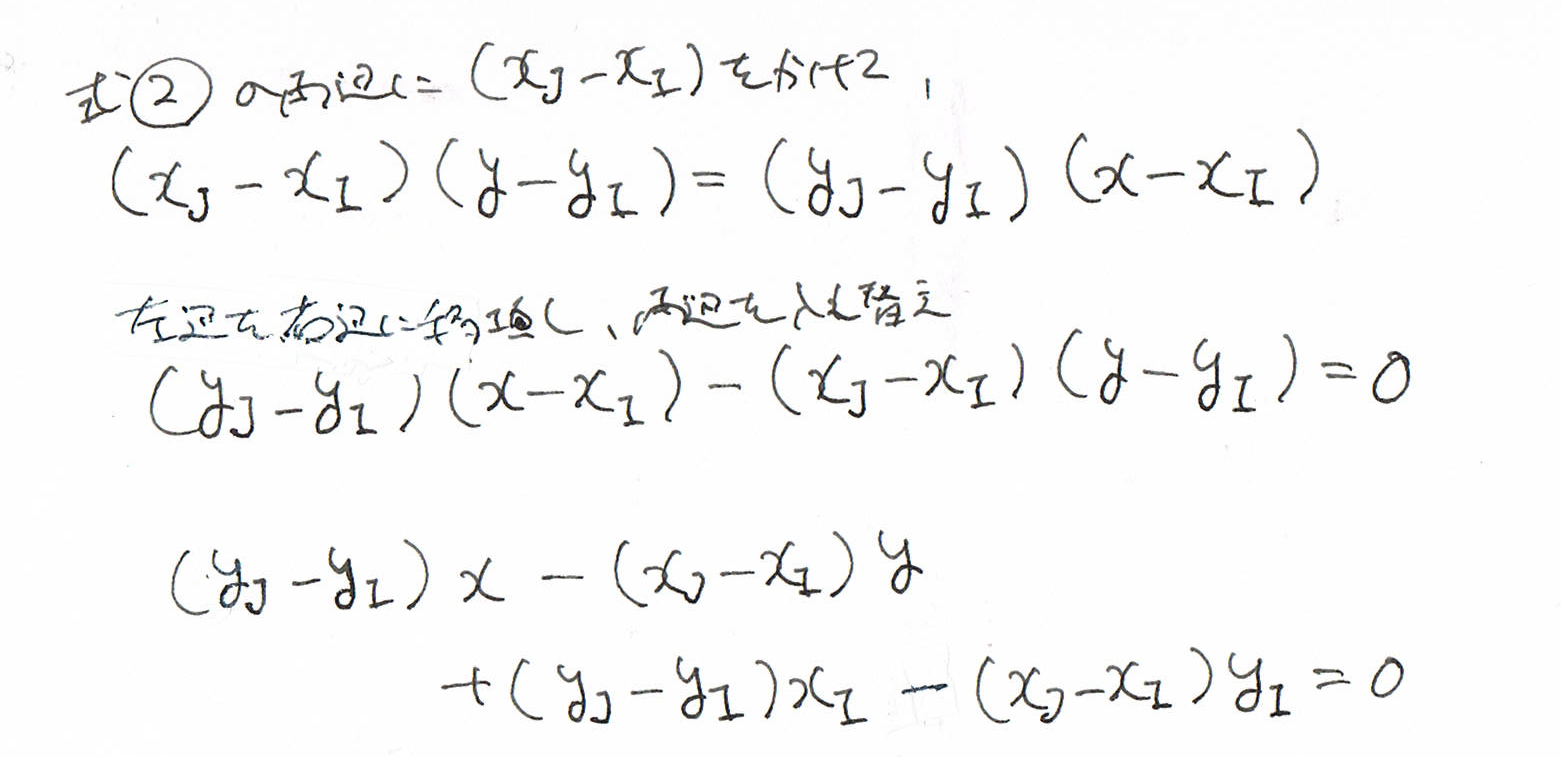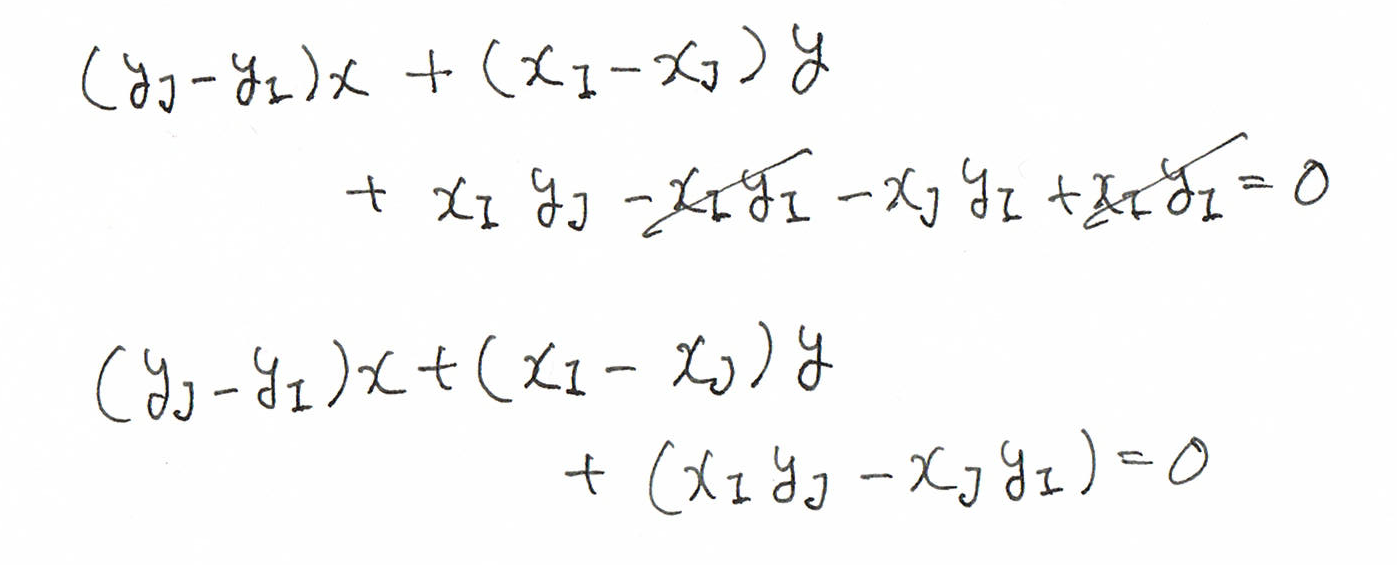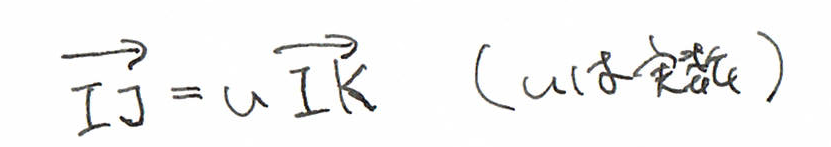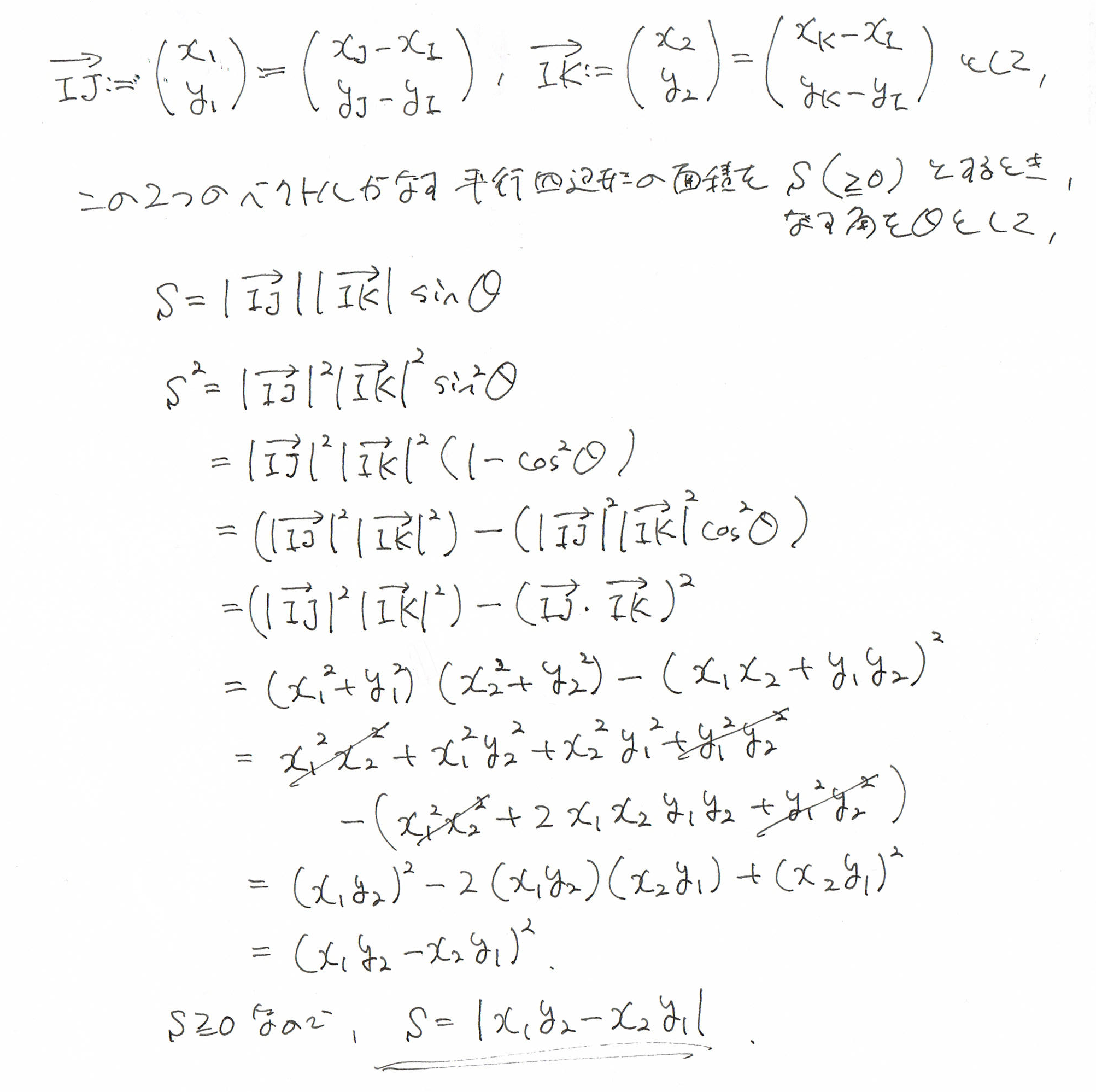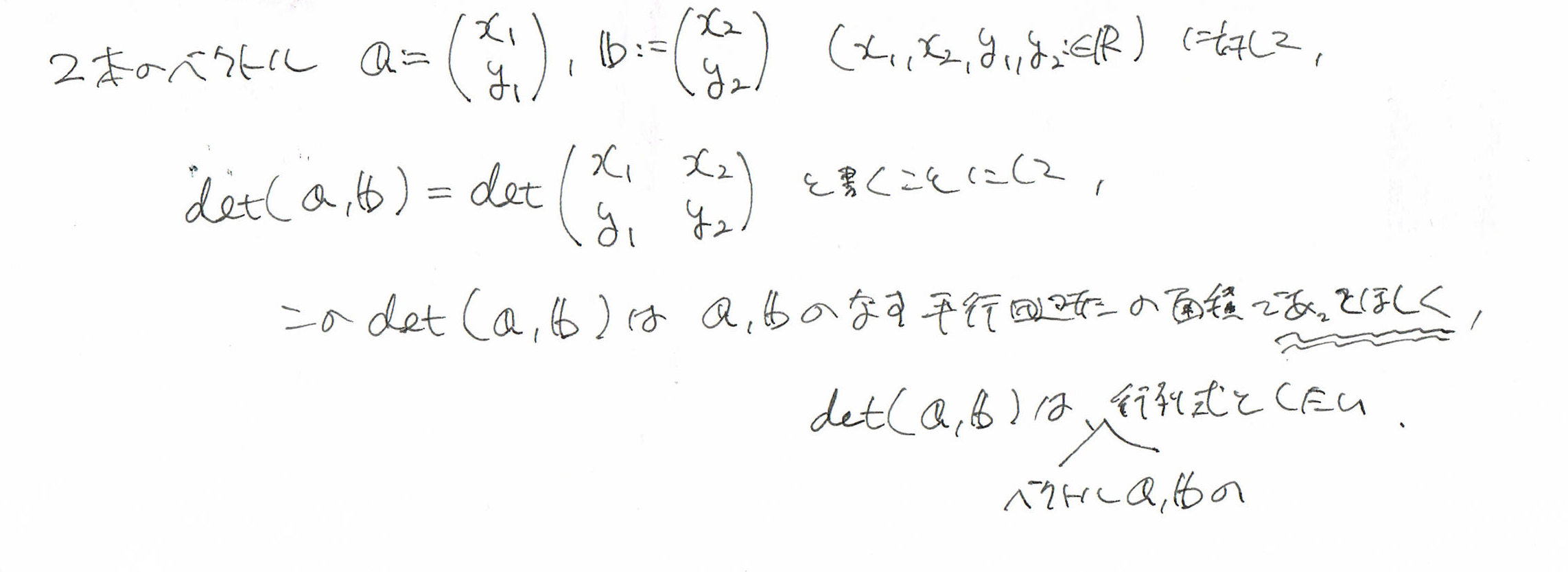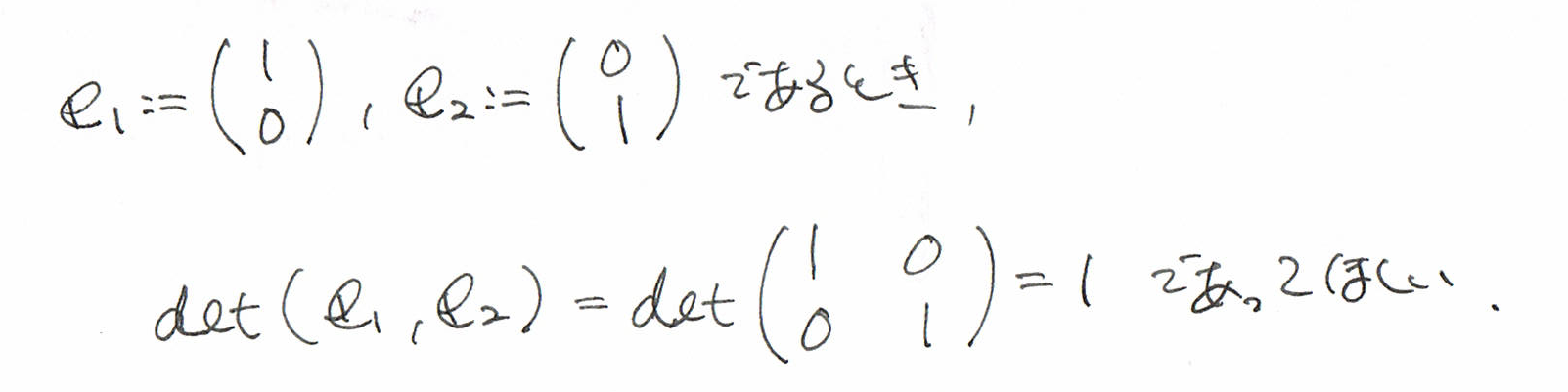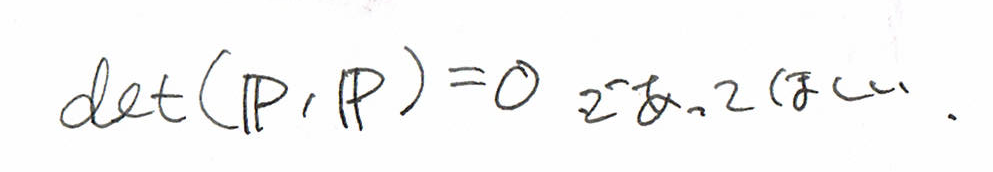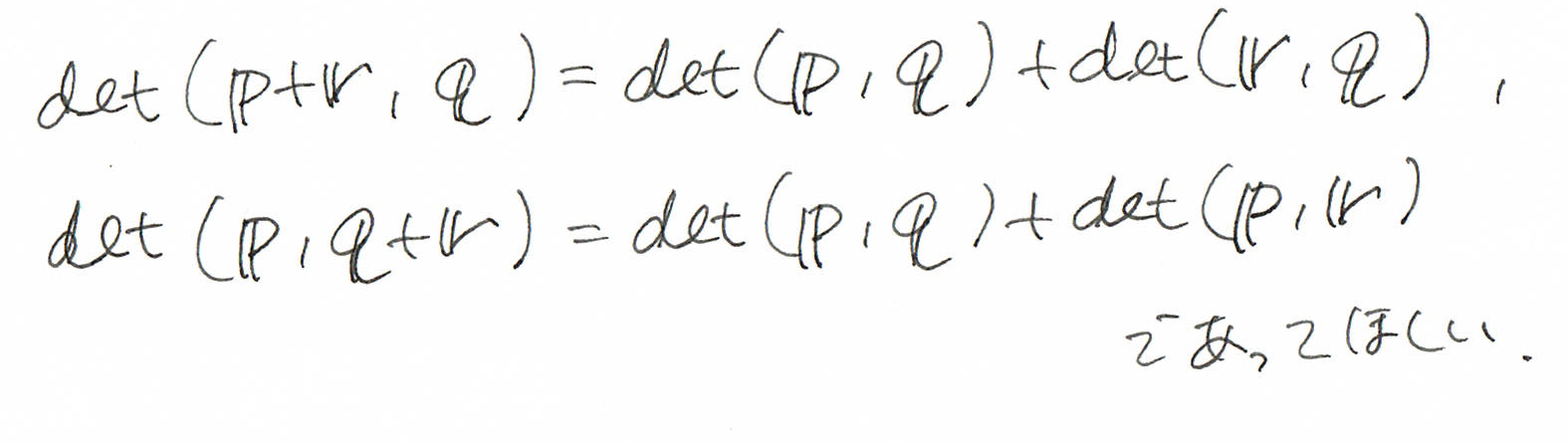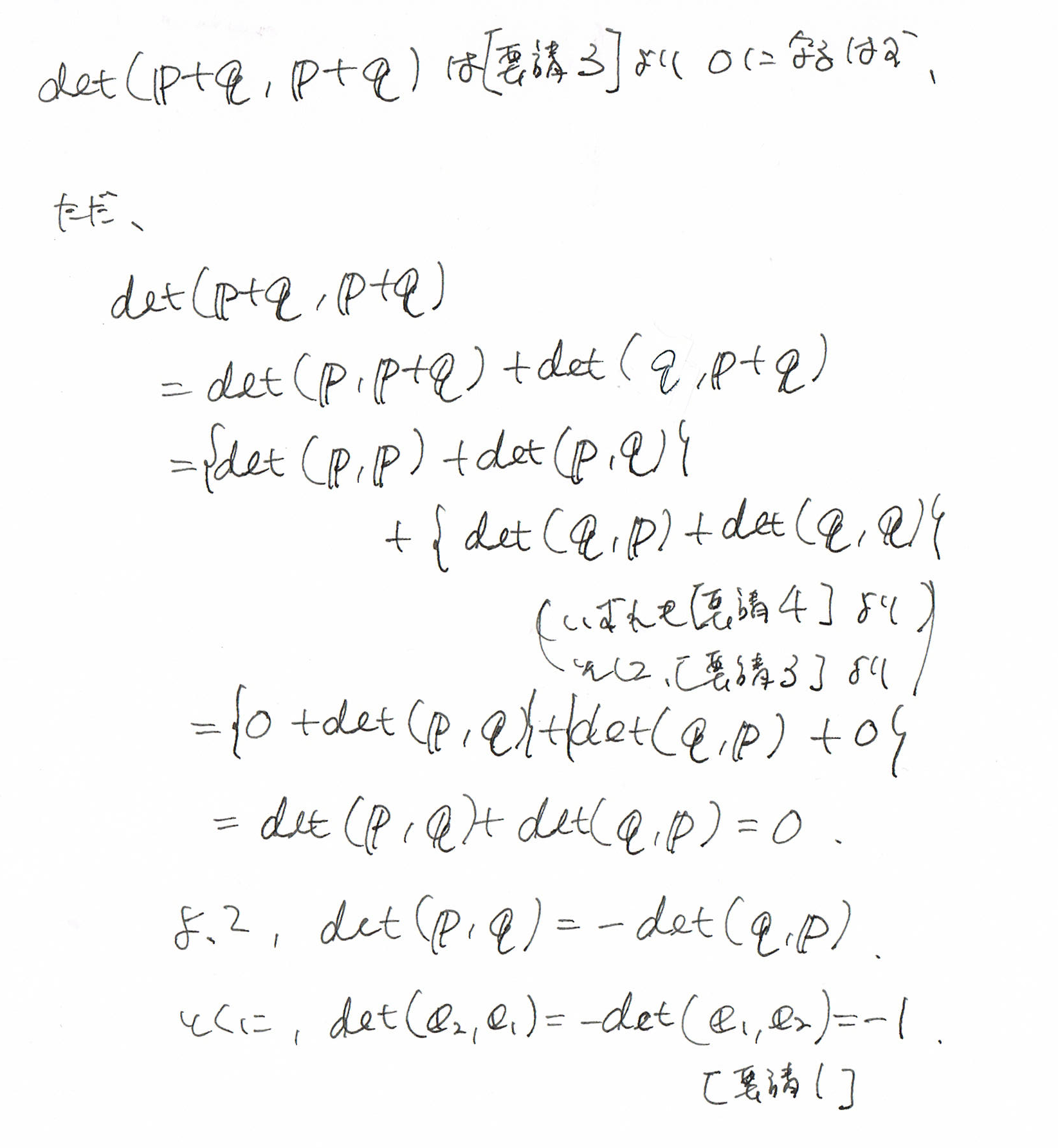♪ジングルベ~ル、ジングルベ~ル、お正~月~、今日は~楽しい、大み~そか、
ヘイヘイヘイ…
さて、いま、聴きたい曲はどっち?
・紅組…マライアキャリーのあの曲
・白組…ワムのラストなんちゃら
と、**「年越しにクリスマス・ソングをかける馬鹿がどこにいるんですか?」**と言った
ピストン西沢さんの名言を思い出しつつ、この記事を書いています。
この記事は、Competitive Programming (1) Advent Calendar 2020に参加しています。
https://adventar.org/calendars/4969
今回、使う問題はこちら、
ABC181 C - Collinearity

はい、このように、ぼくが、本番のコンテストで正解できなかった問題です。
そんなぼくが、今回は、水先案内人となり、
この問題を肴に、中学の1次関数から、高校の幾何学を抜けて大学の線形代数まで、
一気に航海します。
みなさん、泥船に乗った気分で楽しんでいただければ、幸いです。
(いま、船沈むと、海寒いぞ!)
問題概要
$N$個の点の中の相異なる3点であって、同一直線上にあるものは存在するでしょうか?
Yesか、Noかで、お答えください。
($N$は、$3$以上、$100$以下。各点の$x$, $y$座標は、$-1000$から、$+1000$まで)
さて、A,B問題とは違い、本格的に計算量の吟味が必要になってくるのが、C問題。
まず、C問題に欠かせないお約束、計算量をチェックしましょう。
for (int i = 0; i < N; i++)
{
for (int j = i + 1; j < N; j++)
{
for (int k = j + 1; k < N; k++)
{
// (ここに、判定条件が入ります。)
if (?????) // もし、点i, j, kが一直線にあるのなら
{
WriteLine("Yes");
ReadKey();
return;
}
}
}
}
通常は、避けようとする、3重ループですが、所詮、相手の$N$は、高々$100$個。
$100 × 100 × 100$ でも、たったの $1,000,000$通りで、
計算量的には、まったく問題ありません。
勝負は、判定条件にあると見てよさそうです。(←負けた。)
さて、点I, J, Kの3点が、一直線にあることを**「正確に」判定**するには、
どうすればいいのでしょうか?
また、以下、数式部分は、すべて、なんと新型コロナの影響につき(?)
ほぼ、すべて、手書きとなります。
★図形と方程式コース★
まず、直線と聞いて浮かぶのは、
$y=mx+n$の式ですが、(中学校時代だと、$y = ax + b$)
この時代の考え方では、正解にたどり着くのは、難しそうです。
$m$の傾きを求めるのは、中学、高校と一緒ですが…
関係ありそうな公式を一気に導いてみます。
ここまで導くのは、数学的に、もちろん正しいです。
ただ、ここで、2つ大問題があります。
「割り算があるじゃん」(※コンピュータだって、割り算は苦手です。)
「$x_{\rm I} = x_{\rm J}$ のとき、どうするの?」
後者は、高校数学で、ちゃんと解決策が示されていますが、
もっと問題なのは、前者の方。
整数÷整数が、整数とは限らない。
代数学的に言うと、「整数は除法について閉じていない。」
ことが、
小数点以下の小さな誤差となって、われわれを苦しめます。
(Multiplicationなんちゃら、と言っただけで、苦味を感じている人も多いはず。)
これは、シンプルなこの方法で、対処することが可能です。
分母を払った$Ax+By+C=0$も、やはり直線の方程式で、しかも、$x_{\rm I} = x_{\rm J}$のときも使えます。
for (int i = 0; i < N; i++)
{
for (int j = i + 1; j < N; j++)
{
var a = y[j] - y[i];
var b = x[i] - x[j];
var c = x[i] * y[j] - x[j] * y[i];
for (int k = j + 1; k < N; k++)
{
if (a * x[k] + b * y[k] + c == 0)
{
WriteLine("Yes");
return;
}
}
}
}
WriteLine("No");
この方法で、ちゃんと正解が取れます。
★もうちょっと、かっこいい方法でやりたいんですが…★
ただ、ぼく、こんなことも書きました。
昨日のABC181のC問題。
— たかはしよしぴろ @ 誰も知らない存在理由 (@TheYoshipiro) November 2, 2020
「直線の方程式を作る」という考え方に行ってたのが、
マズかった。
各点を始点Iとして、他の2点J、Kとの
2本の「位置ベクトル」で、
行列式 = 0になるものがあるかどうかを、
確かめるっていうのが、
大学で線形代数を学んだ人の回答のはずですわーね。#AtCoder
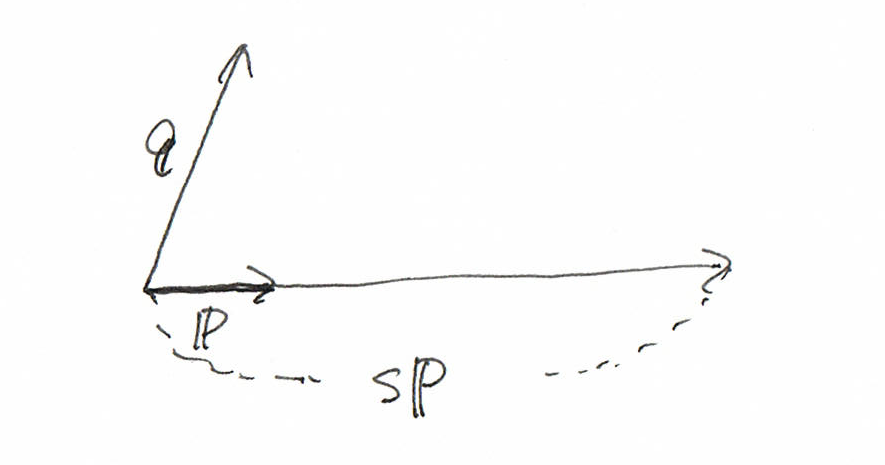
「位置ベクトル」というのは、平たく言うと、数学的に扱いやすいように、
ある一点を原点 $(0, 0)$に持ってくる方法を指します。
そして、その位置ベクトルが
となるとき、ベクトルIJとIKは平行で、点I, J, Kは、一直線にあることがわかります。
ここで、方針が2つ。
- x, yは、どうせ、1000までの整数なのだから、最小公倍数で処理をする
- 2本のベクトルが平行だから、その2本のベクトルがなす、平行四辺形の面積は0になるはず…(←!)
1番目の解き方の方が、たぶん、簡単な気がするのですが、
2番目の解き方の方が、言っているツイートの解き方です。
ただ、あまり、思いつかないと思いますが、行列式をいじっていると思いつきはします。
ここで、ベクトルの解き方を、ホントにザーッと式だけで、紹介します。
さて、そこそこ手間がかかる計算がありましたが、
これは、さっきのツイートでいった行列式で処理をするのと、実は一緒の答えです。
なぜなら、(2次の)行列式を計算するということ自体が、
平行四辺形の面積を求めること、
そのものだから。
ということを、平行四辺形の面積を求めることから考えられる、
行列式の条件を要請していきながら、示していきたいと思います。
(書き方も大学チックな書き方にしているのは、ご了承のほどを)
そりゃあ、底辺1、高さ1で、しかも、なす角が直角な、
1辺が1の正方形は、面積1であって、欲しいですよね。
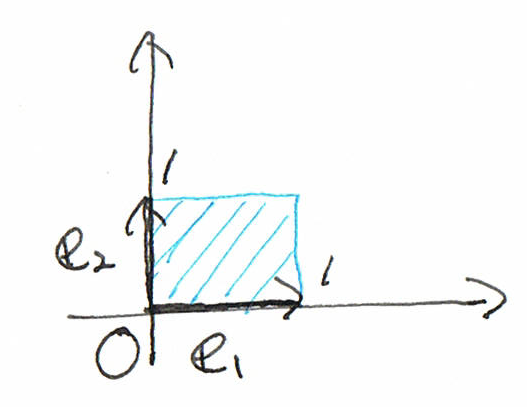
上の式については、下の図を参照。
下の式については、下の図を回転させたり、pとかqとか文字を入れ替えたりしてみてください。
つまらない要請のように聞こえますが、
あとでじんわり効いて来ます。
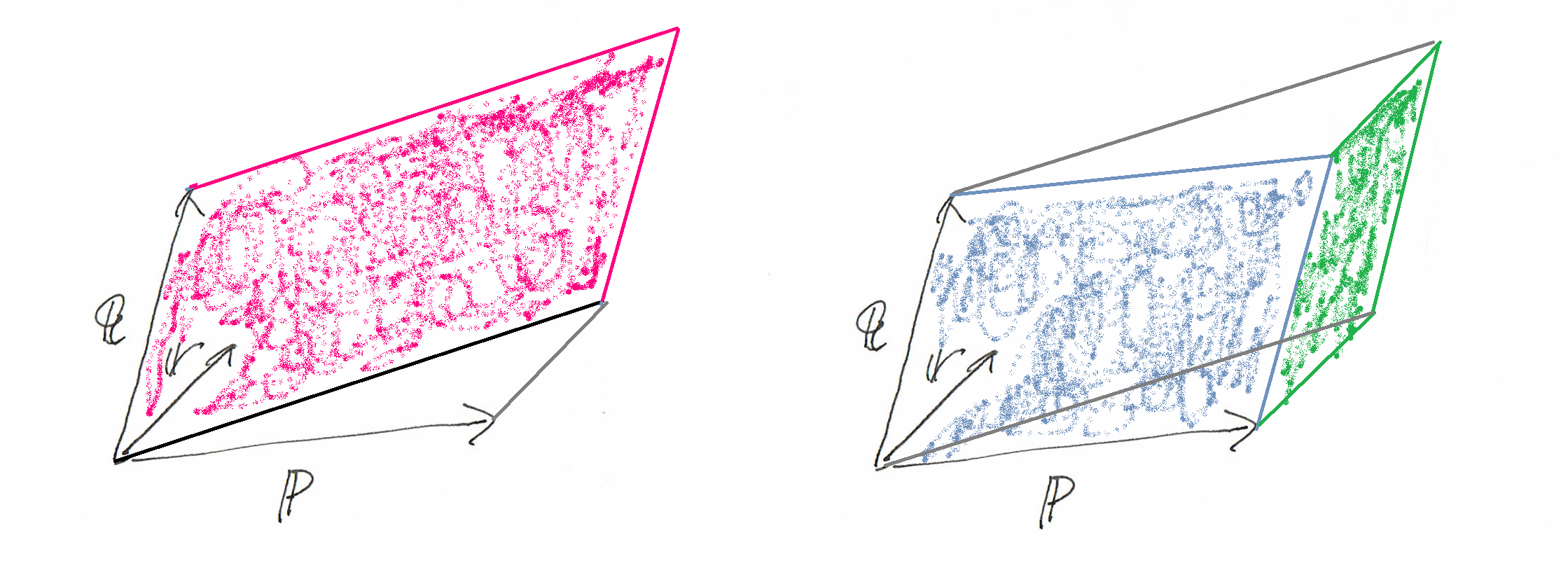
例えば、上の式の
左辺(下左図のピンクの平行四辺形の面積)
=右辺(下右図の青と緑の平行四辺形の面積の合計)
になってることは、おわかりいただけるでしょうか?
さて、以上、あたりまえのことを要請してきたつもりですが、
残念な事実があります。
面積を求めるはずなのに、マイナスの値が出てきました。
ただ、これも認めることにします。
(この問題で欲しいのは、面積が0かどうかだけなので、)
では、2本のベクトルIJ、IKの面積を求めるべく、
行列式の計算してみたいと思います。
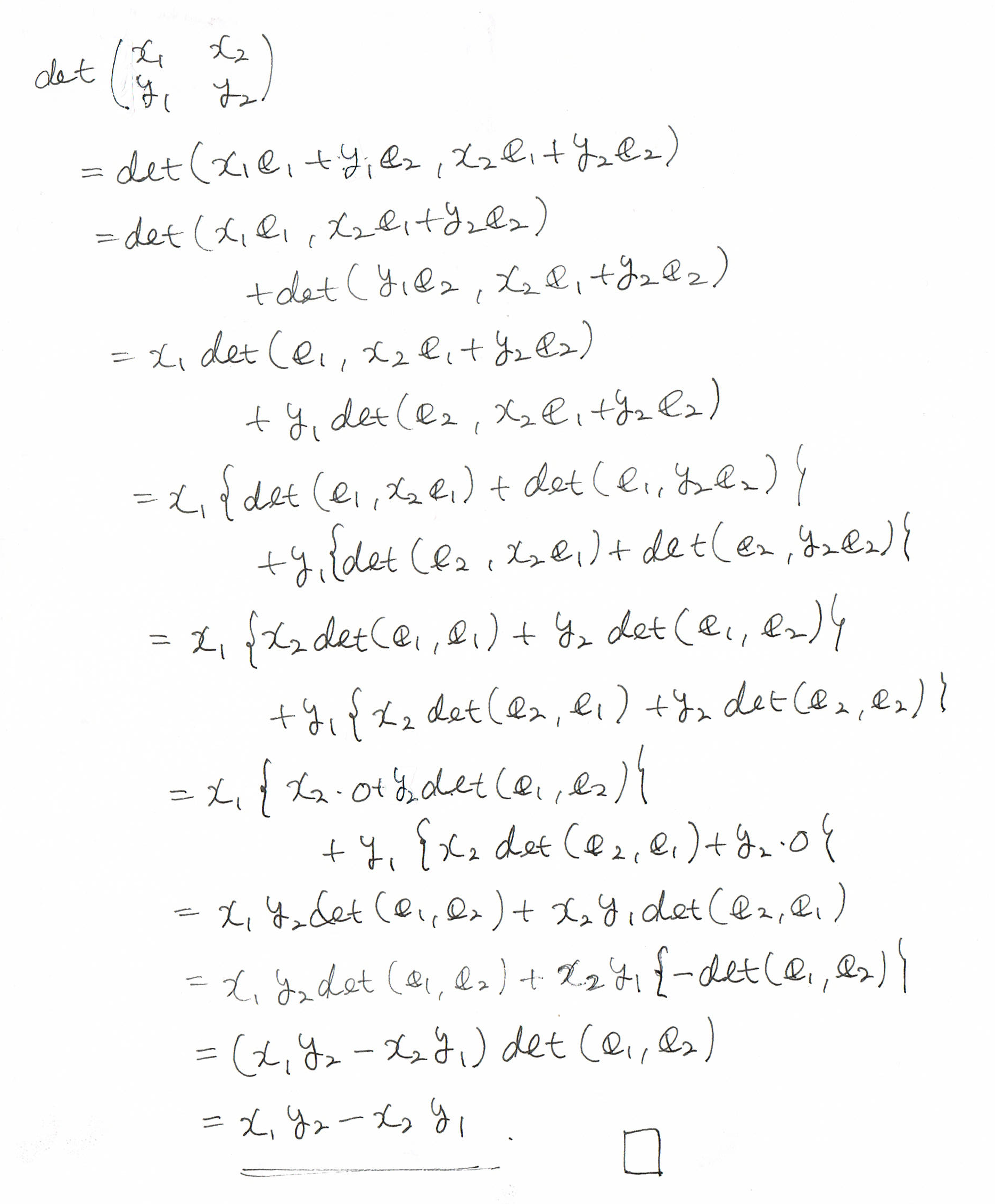
ベクトルで求めたときの平行四辺形の面積が求まりました。
(ただ、こっちは、符号のプラス、マイナスの違いがある可能性だけはありますが。)
for (int i = 0; i < N; i++)
{
for (int j = i + 1; j < N; j++)
{
var x1 = x[j] - x[i];
var y1 = y[j] - y[i];
for (int k = j + 1; k < N; k++)
{
var x2 = x[k] - x[i];
var y2 = y[k] - y[i];
var det = x1 * y2 - y1 * x2;
if (det == 0)
{
WriteLine("Yes");
ReadKey();
return;
}
}
}
}
WriteLine("No");
このコード、もちろん、ちゃんとAC取れます。
https://atcoder.jp/contests/abc181/submissions/17844407
以上で、中学から、大学までの幾何学のつながりを、
なんとか描くことができました。
そして、Advent Calendar
Competitive Programming (1) Advent Calendar 2020
https://adventar.org/calendars/4969
も、クリスマスまでに間に合わせることは別にして、
年内に間に合わせることができました。
上記、Advent Calenderの最後を飾ることができました、
25人全員の記事を上げることができました。
25人の執筆陣を勝手に代表して、読者の皆様に感謝いたします。
それでは、みなさん、来年もよいお年を。(12/31 23:53記す。)