ABC144C - Walk on Multiplication Table のアタマの中分析
Competitive Programming (2) Advent Calendar 2019 19 日目の記事だよ。
この記事は
6題時代になった、AtCoder Beginner Contest(略してABCと呼ばれる)の
ことについて書きたいです。
…とは言っても、ぼくも茶色コーダーの手前、
D問題、E問題、F問題について書くことは一切ありません。
なので、C問題のことについて書きます。
C問題は、簡単なのか、むずいのか
C問題は、大別すると、
・アルゴリズムいらないがパズルっぽい問題と、
・最近では、ここでアルゴリズムの入り口っぽいことを紹介しちゃおうとする
考えもあるような気がする。
で、アルゴリズムについては、まだダンジョンの入り口にも到達していないので、
(通りすがりのゴブリンに場所を訊いたりしているのだが…)
この記事では、前者しか書きません。
C問題の位置づけについては、D問題以降は、天才以外お断りになるからか、
(そんな天才のみなさんが簡単だと言ったりするけれど《天才が束になっているのが、AtCoder界の魔境ぶり》)
実際の順位表上では、ABCだけあって、
ABC3題正解の3完勢がわりと多数を占めたりしていて、
同じ3題正解でも、正解タイムが20分か、60分か、100分かでレートの上がり方も、
パフォーマンスも相当違うという意味で、悲喜こもごもの風景が順位表からでも繰り広げられる場所だったりします。
B問題までは、素直に素朴に書くことが一番大事なのに対して、
C問題は、素直に感じたまま、芸術家になった気分で筆を動かすと、
「TLE」の3文字しか帰ってこないという、
仕様書、詳細設計書にはないコーディングを求められるようです。
そんな難易度がABCのC問題。
九九3部作
**「九九の表でもいろんな問題がつくれるもんだな。」**という
小並すぎる感想を抱いたこの回の問題のC問題を見た時の、
アタマの中を再現してみたいと思います。(実際に解くところまではいかない)
https://atcoder.jp/contests/abc144/tasks/abc144_c
出すまでもないとは思いますが、
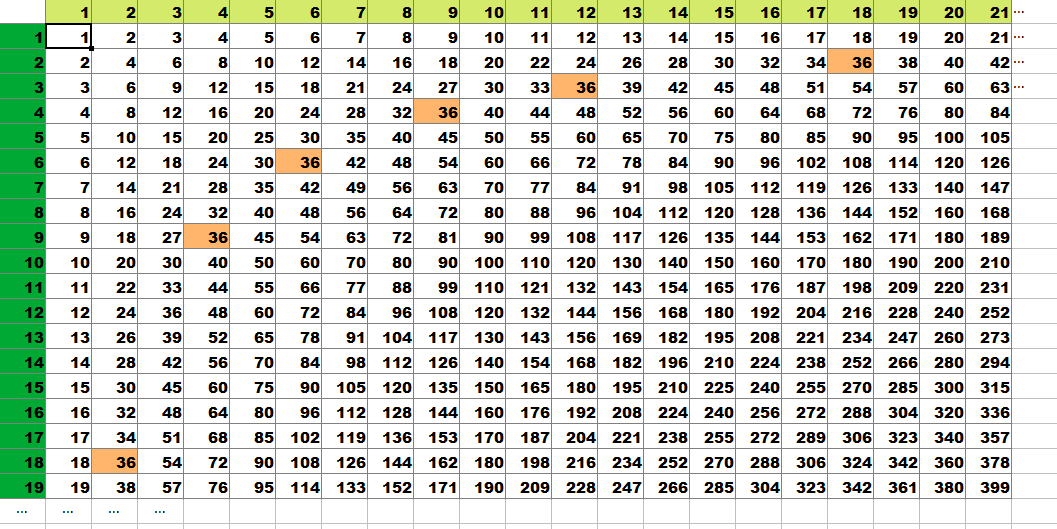
こちらが、みなさんおなじみの九九の表です。
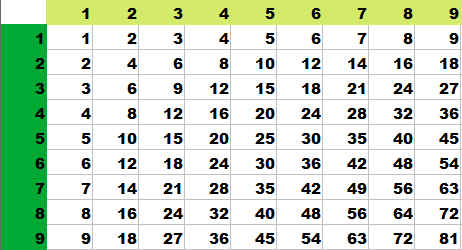
タネも仕掛けもなさすぎるやつです。
縦と横を入れ替えても変わらないことを確認しておきましょう。
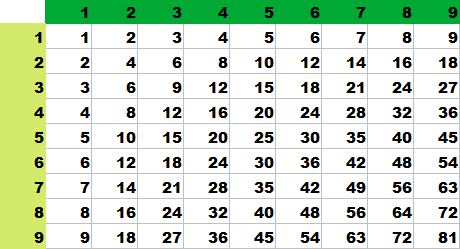
これでは、天下の大マジシャン・マギー司郎先生でも、
日曜夕方5時半の茶の間を沸かせることはできない。
縦じまのハンカチよりも強敵です。
さて、九九81マスありますが、
これ別に1から81までの81個の整数全部があるわけじゃないんですよね。
1から10までは、全部ありますが、
ちょっと上を探すと、11, 13, 17, 19がないですし、
50, 60, 70, 80のどれもありません。
逆に、ダブる数や、トリプる数もいっぱいで、
たとえば、12なんて4か所もありますし、
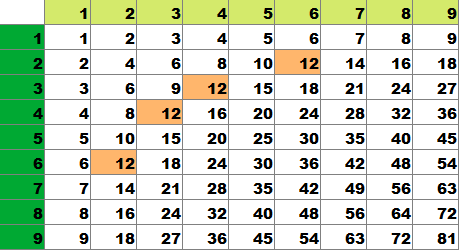
出てくる頻度がバラバラで、それを調べるというのも、
数学(初等整数論、解析数論)の問題意識としてはあります。
ここで、9×9マスに制約していると、
もとの問題が考えづらくなってきた(ような気がする)ので、
表を拡張しただけだと、やはり、どこに注目したらいいかわからないので、
数を1個固定して考えましょう。
そうですね…
36にします。(←あれ?さっきと注目する数、変わったぞ。)
ここで、マークを付けた6か所と、そのほかに、1×36と36×1が隠れているので、
合計8か所になります。
もとの問題からすると、
「高橋くんのいる1×1=1のマスから、一番近くの36まで、歩いて何歩?」
(歩くのは、下か右へのみで、ナナメはダメ)という問題でした。
この表まで落とし込めれば、解くのはもう一歩なのですが、
その前に考えなければいけない重要なポイントがあって、
「表の中で、36がある地点を、どうやって見つけたん?」っていう問題があります。
ここからは、小学2, 3年生からは、少しランクが上がって、
こんな問題になります。
何と何をかけると36になる。 = 36は、何で割れる?
= 36の約数を列挙すると?
という問題になります。
素因数分解するという方法はありますが、それを知らないとしたら、
できることはひとつしかありません。
実際に割ろうとしてみる。
これだけです。
36に対して、割り切れる数を抜き出すと、
1, 2, 3, 4, 6, 9, 12, 18, 36
と9つになります。
…が、ちょっと待った。
最初の方の1, 2, 3は、ずいぶん軽快に割れてたのに、
後ろの方、無駄打ち多くないですか?
9までは、6つヒットしてたのに、そこから先3つしかヒットがないです。
それなのに、合計36回も割り算しています。
それに、この方法、数が大きくなると、問題の条件から、
1兆回割り算(実際は余りの計算ですが)しなきゃいけないって、
間に合わないじゃないですか。
そこで、こう考えます。
36を、たとえば、2で割った18も、やっぱり36の約数。
この考えで、両方セットで求めることができて、(ついでに座標も求まっている)
36は…
1でわって、1と36、《座標は、(1, 36)、(36, 1)、どちらも(1, 1)から歩いて36 歩》
2でわって、2と18、《座標は、(2, 18)、(18, 2)、歩いて、(2-1)+(18-1)=18 歩》
3でわって、3と12、《(3, 12)、(12, 3)まで、(3-1)+(12-1)=2+11=13 歩》
4だと、4と9、《(4, 9), (9, 4)へは、3+8=11 歩》
5では、わりきれなくて
6だと、もう片方も6で、《(6, 6)へは、5+5で10 歩》
たった6回の割り算と、簡単なたし算、ひき算で「10」と求めることができました。
36回の計算が、たった6回に(=√36回で済むように)になりました。
元の問題も、√1兆回 = 100万回の割り算で間に合うようになりましたとさ。
(この問題の場合は、目的の数の座標がある個数も考察しなきゃないですが、
さほど、問題がないで押し通してOKなので、)
これで万事解決、めでたし、めでたしなわけです。
■