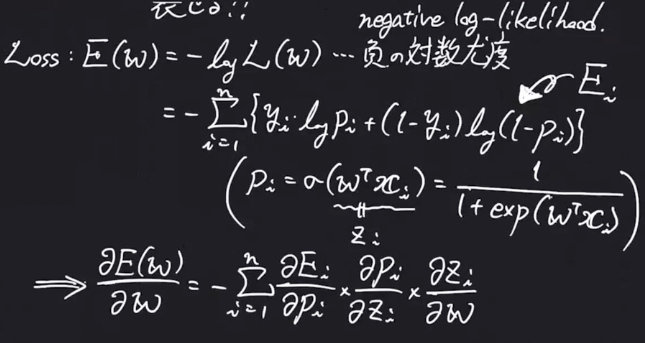本記事は、Study-AI社様のJDLA認定プログラムの提出レポートを兼ねた記事となっております。
機械学習とは
コンピュータープログラムは、タスクTを性能指標Pで測定し、その性能が経験Eにより改善される場合、タスクTおよび性能指標Pに関して経験Eから学習すると言われる（トム・ミッチェル 1997）
- あるコンピュータープログラムにデータを入力しタスクTを解かせるとする
- 未知データを入れると出力Y1が出る
- 出力Y1を性能指標Pで測ることが出来る
- 更に新しいデータを入力し出力Y2を出す
- 性能指標Pにより測定した際、Y2がY1より改善されていた場合、このコンピュータープログラムは学習したと言える
線形回帰
- 線形とは？＝ざっくり「比例」
$$
e.g: \space
y=Ax + B (2次元)\
z= Ax + By + C (3次元)
$$ - n次元空間における超平面
$$
\begin{align}
y &= a_0 + a_1x_1 + a_2x_2 + \cdots + a_{n-1}x_{n-1} \
&= a_0 + \sum_{i=1}^{n-1} a_ix_i \
&= \sum_{i=0}^{n-1} a_ix_i,where \space x_0 \equiv 1\
&= \boldsymbol{a}^T \boldsymbol{x} \space (n次元ベクトル)
\end{align}
$$
###回帰問題
- 説明変数(入力)
$$ \boldsymbol{x}=(x_1, x_2, ・・・,x_m)^T \in ℝ^m$$ - 目的変数(出力)
$$ y \in ℝ^1 (yは実数) $$
###線形回帰モデル
- 回帰問題を解くための機械学習モデルの一つ
- 教師あり学習
- 入力とm次元パラメータの線型結合を出力するモデル
- 予測値にはハットを付ける（教師データのyと区別）
**教師データ** $$ {(\boldsymbol{x_i}, y_i) ; i = 1, ... , n} $$ **パラメータ**（入力変数と同じ次元数） $$ \boldsymbol{w} = (w_1, w_2, ... , w_m)^T \in ℝ^m $$ **線型結合**（未知のパラメータwと入力xの内積） $$\hat{y} = \boldsymbol{w}^T \boldsymbol{x} + w_0 = \sum_{j = 1}^{m} w_jx_j + w_0 $$ * 目的: wの値を決定する
###線形結合
- 未知のパラメータwと入力xの内積の総和
- 切片w_0も足し合わせる(切片＝y軸との交点、y軸に向かって平行移動するような作用がある)
- 入力ベクトル$x_j$が多次元でも出力は１次元（スカラ）になる
モデルのパラメータ
- モデルに含まれる推定すべき未知のパラメータw
- 特徴量が予測値に対してどのように影響を与えるかを決定する重みの集合$w_j$
- 最良の勾配を最小二乗法により推定する
####単回帰モデル
- 説明変数が１次元(m=1)
- データは回帰直線に誤差が加わり観測されていると仮定
- 偶発誤差かの見極め
- y (来店者数) が$x_1$(気温) と $x_2$ (曜日) で決まると仮定する。
- 気温だけで来店者数を予測しようとすると、曜日の情報は$\epsilon$(誤差)に乗る。
- 誤差が大き過ぎる場合、説明変数が不足していると考察できる。
- 連立方程式をベクトルで表すと、
- 実装面において行列の shape の確認は重要
####重回帰モデル
- 説明変数が多次元(m>1)
- 単回帰は直線、重回帰は局面・超平面
- データは回帰局面に誤差が加わり観測されていると仮定
- 基本的にデータ数xよりパラメータ数wが多い問題は解き難い
データの分割
- 目的：汎化性能を測る（未知データに対しての精度の良さ）
- 線形回帰モデル
- 平均二乗誤差 (残差平方和)：データとモデルの二乗誤差の和
- 最小二乗法
- 学習データの平均二乗誤差を最小とするパラメータを探索する（勾配０＝最小）
$$ MSE_{train} = \frac{1}{n_{train}} \sum_{i=1}^{n_{train}}(\hat{y_i}^{(train)} - y_i^{(train)})^2 $$
- 学習データの平均二乗誤差を最小とするパラメータを探索する（勾配０＝最小）
- 二乗誤差を用いる際は、外れ値が無いことを確認する(外れ値に引っ張られて傾きが異常になる)
- Huber損失、Tukey損失を用いれば外れ値に対してロバストなパラメータ推定ができる
- wの関数であり、予測値の中に求めるべき変数wは含まれることに注意
- J(w)を最小化するwを求める
- $arg \space min \space MSE$は「MSEを最小化する入力」を求めろの意
- 内積の形は$\Sigma$の形に直せる
- 新たな入力Xに上で算出した回帰係数$\hat{w}$をかけると予測$\hat{y}$ができる
非線形回帰モデル
- パラメータwに関しては線形のまま
- 重みについて線形でも(linear-in-paarameter)、十分非線形な関数を表すことができる
基底関数
- 基底展開法
- 回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用
- 未知パラメータは線形回帰モデルと同様に最小二乗法や最尤法により推定
- xを一旦線形の写像$\phi$によって非線形化して、wとの内積を求める
$$ y_i = f(x_i) + \epsilon_i $$
$$ y_i = w_0 + \sum_{i=1}^{m}
w_i\phi_j(x_i) + \epsilon_i $$ - 基底関数の例：多項式関数、ガウス型基底関数、（B）スプライン関数など
- ガウス型基底関数
- exp(-x) はxが大きくなると指数関数的に小さい値を返す
- xからの距離が近い方の山の値は大きく、遠い山は小さい値をとる
- 次元を大きくしてガウス型基底関数を増やすことができる
- X が $\Phi$空間に飛ばされた場合を考える
１次元の基底関数に基づく非線形回帰
- 多項式（１〜９次）
$$\phi_j = x^j$$
- ガウス型基底
$$ \phi(x) = exp{\frac{(x - \mu_j)^2}{2h_j}}$$- 正規分布の形なので、積分した時に１になる
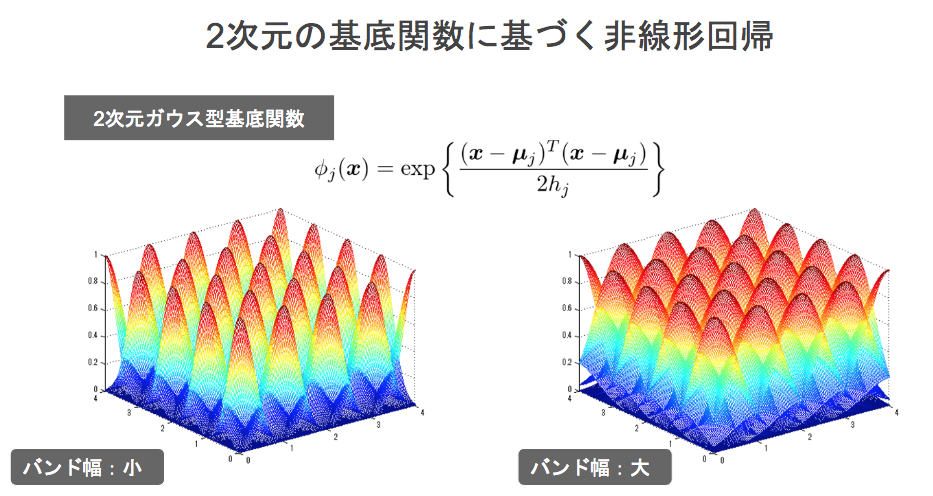
- 正規分布の平均の場所、ある山がどれくらい広がるかをバンド幅というパラメータによって規定される→２次元の基底関数に使える
２次元の基底関数に基づく非線形回帰
- ２次元ガウス型基底関数
$$\phi_j(x) = exp{\frac{(x - \mu_j)^T(x - \mu_j)}{2h_j}}$$- 基底関数をデータ空間上に配置可能
基底展開法
- 説明変数
$$ x_i =(x_{i1}, x_{i2}, ・・・,x_{im}) \in ℝ^m $$
説明変数を基底関数ベクトルに変換（xを、事前に用意されているK個の写像$\phi$で変換）して、、、 - 非線形関数ベクトル（K次元特徴ベクトル）
$$ \phi(x_i) = (\phi_1(x_i), \phi_2(x_i), ・・・ , \phi_k(x_i))^T \in ℝ^k$$
iがn個分（学習データ分）存在するので、写像を学習データにすればk次元のパラメータベクトルがn個出てくる。これにより計画行列が求められる - 計画行列
$$\Phi^{(train)} = (\phi(x_1), \phi(x_2), ・・・ , \phi(x_n))^T \in ℝ^{n*k} $$
後は最尤法を使って予測値を求める - 予測値
$$\hat{y} = \Phi(\Phi^{(train)T}\Phi^{(train)})^ {-1}\Phi^{(train)T}y^{(train)}$$
過学習と未学習
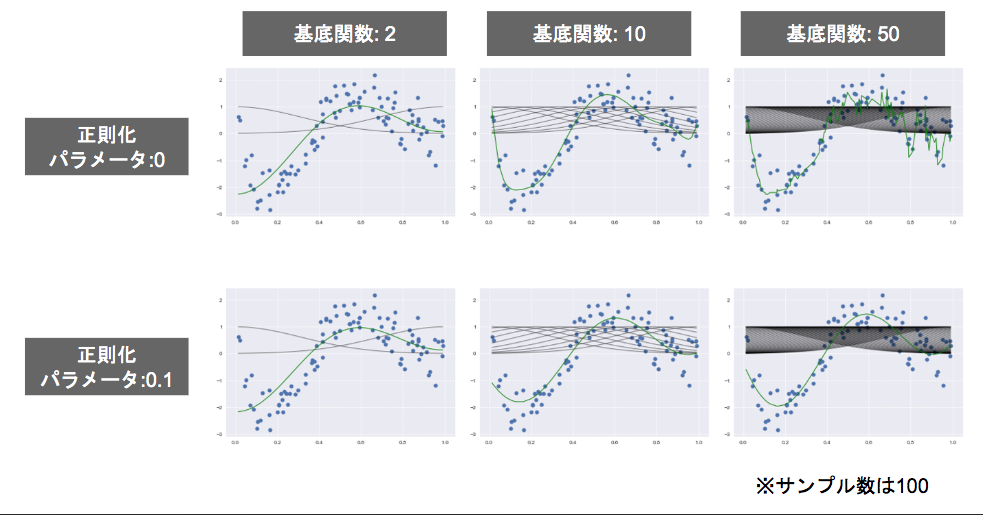
- 未学習（underfitting）の対策
- モデルの表現力が低いので、表現力の高いモデルに変える
- 過学習（overfitting）の対策
- 学習データを増やす
- 不要な基底関数（変数）を削除 (特徴量選択)
- ドメイン知識やAIC(赤池情報量基準)など情報量基準などによるモデル選択が重要
- 正則化 (wのコントロール)
- 係数を小さくされた関数はほぼ無視される
- ｗがあまりにも大きくなる場合に働く罰則項を加える
- 正則化について
- 正則化法 (罰則化法)
- 罰則を与えてモデルの複雑化を抑える
$$ S\gamma = (y - \Phi w)^T(y - \Phi w) + \gamma R(w) $$
- 罰則を与えてモデルの複雑化を抑える
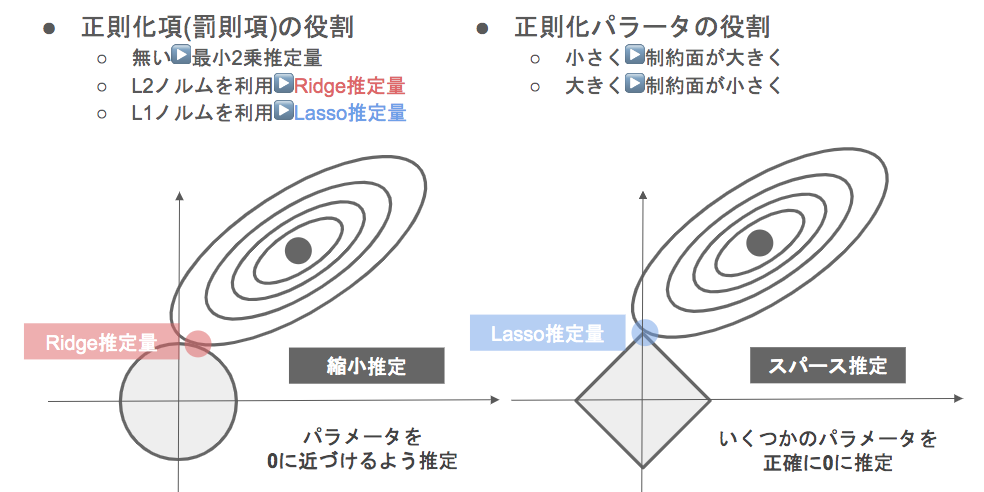
- 正則化項Rの役割
- R無し・・・最小二乗推定量
- L2ノルム・・・Ridge推定量（○型、縮小推定）：パラメータに原点付近に制約を与え、制約の中でMSEを最小にする点を探す
- L1ノルム・・・Lasso推定量（◇型、スパース推定）：MSEを最小化する接点はカドになる、いくつかのパラメータ（$w_i$）を正確に０に推定する。推定する段階で不要な基底・変数を排除できる（説明変数が多い場合、推定１回で予測に対する影響の小さい変数を０にしてくれることは役に立つ）
- パラメータ$\gamma$ = 制約面の大きさ
- $\gamma$を小さくする→制約面が大きくなる
- $\gamma$を大きくする→制約面が小さくなる
- どのように正則化項を入れるか
- min MSE s.t. $R(\boldsymbol{w} \leq \gamma)$
- 不等式条件のついた最適化。KKT条件を用いると min MSE + $\lambda R(\boldsymbol{w}) $ となり、MSEに第二項をつけることで不等号条件を回避できる
- 適切なモデルの選定
- ホールドアウト法
- データが大量にないと、良い性能評価を与えない (データが少ないと外れ値が検証データに含みやすい＝外れ値にフィットするモデルになってしまう)
- クロスバリデーション（交差検証法）
- イテレータ毎に学習用・評価用に分割
- CV値（精度の平均）がホールドアウトで検証したモデルより低くても、汎化性能が高いとは限らない
- 精度の計算は二乗誤差 (原則は学習と検証は同じ損失関数)
- 実務において、精度は検証データ(手元にないデータ)で測ったものを報告する
- ハイパーパラメータ調整法
- グリッドサーチ
- ハイパーパラメータの組み合わせの候補を予め用意しておいて、組み合わせ毎に確かめておく
- Bayesian Oplimization (ベイズ最適化)
- ニューラルネットワークで使うパラメータ調整
- ニューラルネットワークで使うパラメータ調整
ロジスティック回帰
データ形式
- 分類問題 (クラス分類)
- 説明変数(入力)
$$ x=(x_1, x_2, ・・・,x_m)^T \in ℝ^m$$ - 目的変数(出力)
$$ y \in {0, 1}$$
- 識別的アプローチ：
- $ P(C_k | \boldsymbol{x}) $ を直接モデル化
- 識別的アプローチのメリット
- xが与えられた時クラスkに割り当てられる確率がわかる
- 確率で与えられるので判断を保留できる
- 生成的アプローチ：
- $P(C_k)$ と $P(\boldsymbol{x} | C_k)$をモデル化し、その後ベイズの定理を用いて$P(C_k | \boldsymbol
{x})$ を求める - 生成的アプローチのメリット：外れ値の検出ができる
ロジスティック回帰モデル
- ロジスティック線形回帰モデル
- 欲しい出力 y は{0, 1}
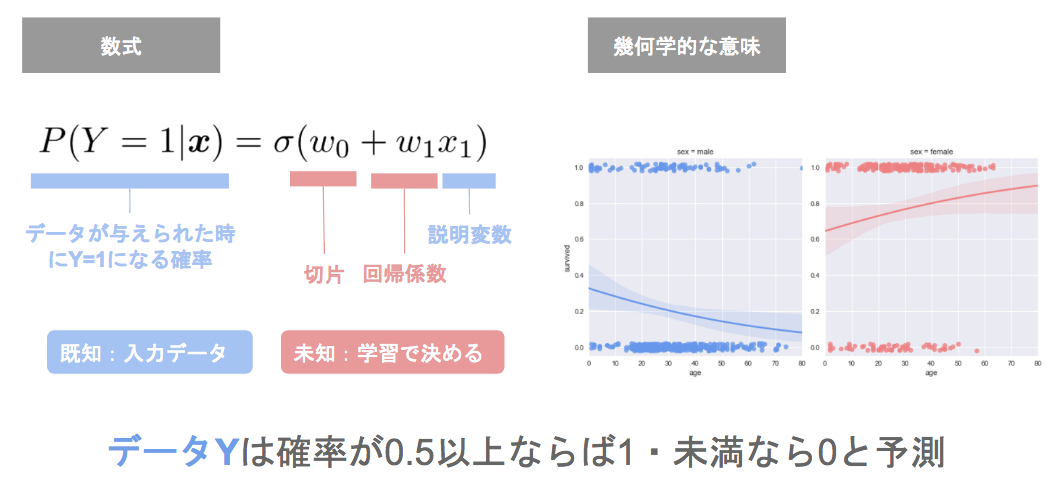
- 実数全体をとる$\boldsymbol{x}^T \boldsymbol{w}$を、{0, 1}に潰す関数を利用
- 入力とm次元パラメータの線型結合を、シグモイド関数に出力
- 出力はy=1になる確率の値になる
-
シグモイド関数
-
シグモイド関数の性質
- シグモイド関数の微分は、シグモイド関数自身で表現できる
- モデルのパラメータ推定においては、MSEや尤度などの基準を最小・最大にする点を求める必要がある→微分が簡便にできることは有利
$$
\begin{align}
\frac{\partial\sigma(x)}{\partial x}
&= \frac{\partial}{\partial x} \biggl(\frac{1}{1 + exp(-ax)}\biggr) \\
&= (-1)・{1 + exp(-ax)}^{-2}・exp(-ax)・(-a) \\
&= \frac{a・exp(-ax)}{ {1 + exp(-ax)}^2}
= \frac{a}{ 1 + exp(-ax)} ・ \frac{1 + exp(-ax) - 1}{ 1 + exp(-ax)} \
&= a \sigma (x)(1 - \sigma(x))
\end{align}
$$
- 求めたい値
$$ P(Y = 1|x) = \sigma(w_0 + w_1x_1 + \cdots + w_mx_m) $$- 線型結合のwxのみでは分類の出力としては不味いので、シグモイド関数$\sigma$をかませて0~1の出力に直している
- 線型結合のwxのみでは分類の出力としては不味いので、シグモイド関数$\sigma$をかませて0~1の出力に直している
パラメータ推定
- ベルヌーイ分布
- 正規分布、一様分布など、様々な分布モデルの内の一つ
- ロジスティック回帰モデルではこれを利用
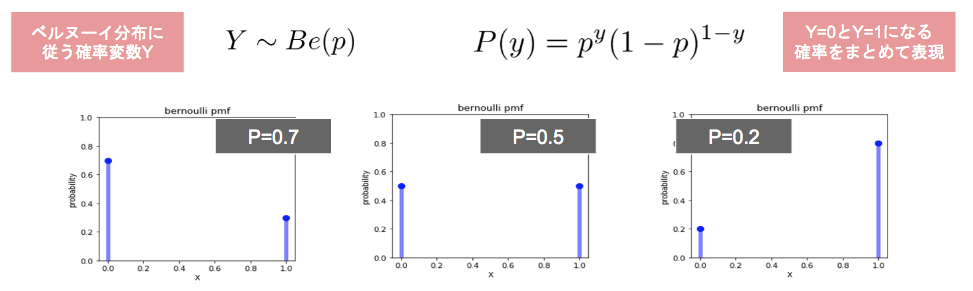
- 離散確率分布（確率p → 1, 確率1 - p → 0）
$$P(y)=p^y(1-p)^{1-y}$$
- 最尤推定（データから尤もらしいPは何か、を推定する）
- 同時確率
- それぞれの確率変数が独立→確率同士の掛算
- 尤度関数
- データは固定し、パラメータを変化させる
- 尤度（likelihood）＝ 対象となる集団$\mu$から特定のサンプル$x_k$を取り出してくる確率
- 確率の対数をとったもの＝尤度関数
- 尤度関数を最大化するようなパラメータを選ぶことを尤度推定という
- ロジスティック回帰モデルの最尤推定
- 線型結合をシグモイド関数を通した確率Pを使って、尤もらしいパラメータwを求める
- 尤度関数Lを最大化するパラメータを探索
- 実用上重要：尤度関数Lは確率Pの積集合。つまり０〜１の値を掛け合わせたものなので、予め対数をとっておくことで桁落ちを防げる。
- 勾配降下法
- 反復学習によりパラメータの逐次的更新を行うアプローチの一つ
- $\eta$は学習率と呼ばれるハイパーパラメータで、モデルのパラメータの収束し易さを調整
- 勾配降下法のメリット：
- 線形回帰モデル (最小二乗法)：MSEのパラメータに関する微分を解析的に求めることができる
- ロジスティック回帰モデル (最尤法)：対数尤度関数をパラメータで微分して０になる値を求める必要があるのだが、解析的にこの値を求めるのは困難
$$w(k+1) = w^{k} - \eta \frac{\partial E(w)}{\partial w}$$
- Eをwで微分する前にPが出てくるのでPで微分 → Pはシグモイド関数なのでzで微分 → zはwとxの線型結合なのでwで微分
- パラメータが更新されなくなった場合、それは勾配が０になったということ。少なくとも反復学習で探索した範囲は最適な解が得られたということ
$$w^{(k+1) = w^{(k)} + \eta \sum_{i=1}^{n}(y_i - p_i)x_i}$$ - 勾配降下法のデメリット：
- 勾配降下法ではパラメータ更新にN個全てのデータに対する和を求める必要がある → メモリ不足、計算時間が膨大になる等の問題がある → SGDを利用
- 確率的勾配降下法 (SGD)
- データを一つずつランダムに（確率的に）選んでパラメータを更新
- 勾配降下法でパラメータを１回更新するのと同じ計算量でパラメータをn回更新できるので効率よく最適解を探索可能
- パラメータの更新がある程度不規則になり（勾配降下法に比べて）初期値に近い局所最適解に陥りにくい（ロジスティック回帰では山が一つなのであまり関係無い）
$$w(k+1) = w^k + \eta (y_i - p_i)x_i$$
モデル評価
- 混同行列(confusion matrix)
- 各検証データに対するモデルの予測結果を４つの観点(表)で分類し、それぞれに当てはまる予測結果の個数をまとめた表
- 分類の評価方法
- 「正解率」がよく使われる
- 正解した数 / 予測対象となった全データ数
- 問題：分類したいクラスにそれぞれ偏りがあることが多い
$$\frac {TP+TN}{TP+FN+FP+TN}$$
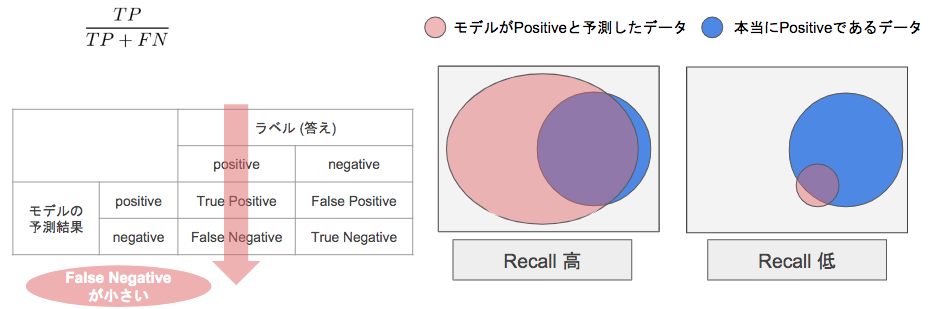
- 再現率（Recall）
- 「本当にPositiveなもの」の中からPositiveと予測できる割合
- 例：病気の検診（見落としはNG）
$$\frac{TP}{TP+FN}$$
- 適合率（Precision）
- モデルがPositiveと予測したものの中で「本当にPositive」である割合
- スパムメール（見落としは多少あってもいい）
$$\frac{TP}{TP+FP}$$
- F値
- Recall と Precision の調和平均
- 高ければ高いほど、Recall と Precision の値も高くなる
主成分分析 (PCA)
次元圧縮
- 多変量データの持つ構造を、より少数個の指標に圧縮
- 情報の損失はなるべく抑えたい
- 少数変数（２・３次元程度）で分析や可視化が可能
- 学習データ
$$ x=(x_1, x_2, ・・・,x_m)^T \in ℝ^m$$ - 平均（ベクトル）
$$ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i $$ - データ行列
$$ \bar{X} = (x_1 - \bar x, ... , x_n - \bar x)^T \ (原点周りで分散するように中心化してやる) $$ - 分散共分散行列
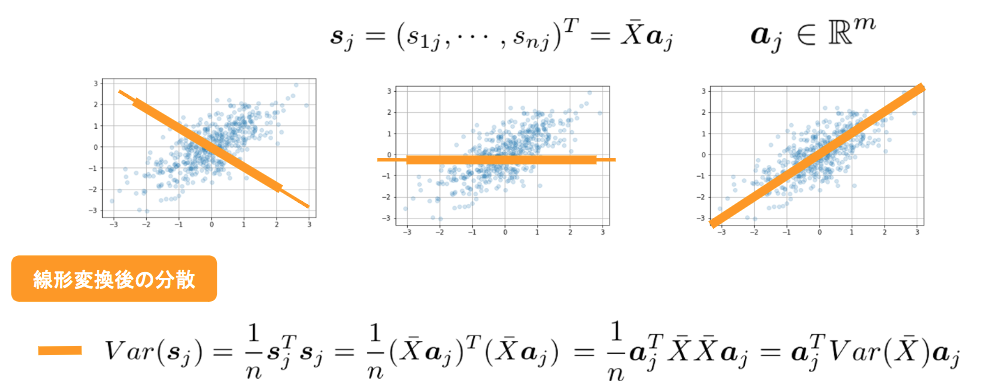
$$ \sum = Var(\bar{X}) = \frac1n \bar{X}^T \bar{X}$$ - 線形変換後のベクトル
$$ s_j = (s_{1j}, ... , s_{nj})^T = \bar{X}a_j, \space (a_j \in ℝ^m) $$- (n個のデータの未知パラメータwを、共通のaで変換したもの→s)
- (jは変換先の次元数 ３次元→ 1 or 2 次元など、軸のインデックス）
- 変換後のデータ$s_j$の分散を最大化することで情報の損失を抑えることができる
- 次元圧縮の目的：線形変換後の変数の分散が最大になるような写像軸を探索する
制約付き最適化問題
K近傍法 (KNN)
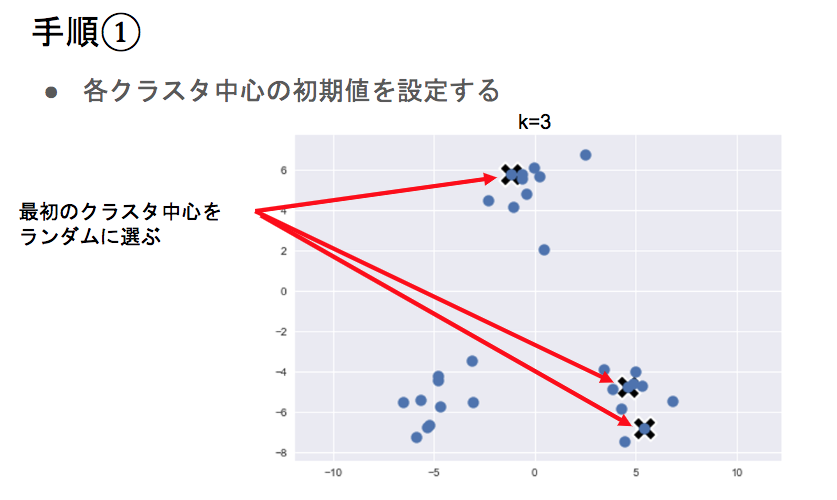
K-平均法 (k-means)
- アルゴリズム：
- クラスタ中心の初期値を設定
- 各データ点に対して、各クラスタ中心との距離を計算し、最も距離が近いクラスタを割り当てる
- 各クラスタの平均ベクトル（中心）を計算する
- 収束するまで2,3の処理を繰り返す
- 初期値が近いと上手くクラスタリングできない点に注意
- kの値により結果も変わる→kの値の設定が肝
サポートベクターマシン
概要
- サポートベクトルマシン(SVM)は、主に２クラス分類に用いられるアルゴリズムである。SVMは、ロジスティック回帰とは異なり、データとのマージンが最大となる識別面を学習によって獲得する。このとき、識別面を構成するために使われるデータをサポートベクトルと呼ぶ。マージン最大化は、ある学習について不等式制約のもとでの最適化問題を解くことで得られるが、その学習データが線形分離不可能な場合、全ての制約を満たす解を得ることができない。そこで、スラック変数を導入することで、誤りをある程度許容しつつ、マージンを大きくとった識別面を得ることができる。このようなスラック変数を導入したSVMはソフトマージンSVMと呼ばれる。
SVMの適用範囲
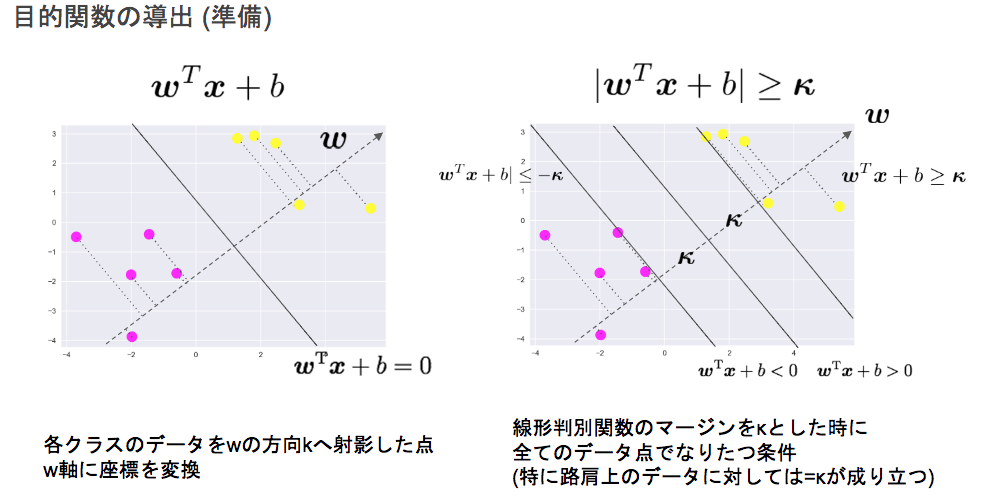
- 線形モデルの正負で２値分類
$$ y = \boldsymbol{w}^T \boldsymbol{x} + b = \sum_{j=1}^{m} w_j x_j + b $$ - 線形分離の決定境界は無数に考えられる
- マージンにより決定
- マージン：線形判別関数$\boldsymbol{w}^T \boldsymbol{x} + b = 0$と最も近いデータ点との距離
- 弱点：計算コストが大きく大規模なデータセットには向かない
- 決定境界
- ２次元：１つの直線で分割
- n次元：n-1次元の超平面（分離超平面）で分割
- この分離超平面に最も近いデータをサポートベクトルと呼ぶ
目的関数の導出
主問題と双対問題
- SVMの主問題
- 主問題の目的関数と制約条件
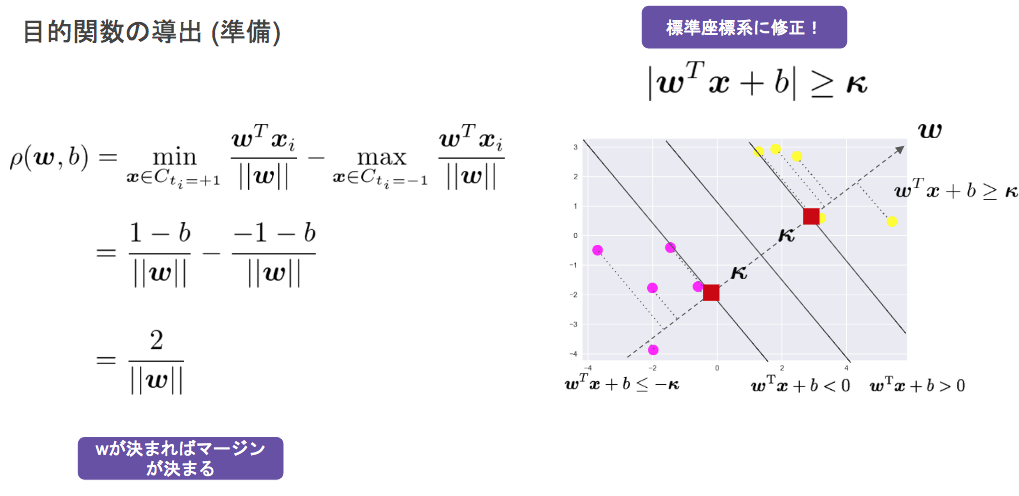
$$min_{w, b} \frac12 ||\boldsymbol{w}||^2 \
t_i(\boldsymbol{w}^T \boldsymbol{x}_i + b) \geq 1 \space (i = 1, 2, \cdots , n) $$- 上の最適化問題をラグランジュ未定乗数法で解くことを考える
- 最適化問題は多くの場合、主問題を直接解かずにこれを双対問題と呼ばれる別の形の数式に変換して、その数式を解くことで最適化問題を解く、ということをする
- ラグランジュ未定乗数法とは
- 制約付き最適化問題を解くための手法
- 制約$g_i(x) \geq 0 (i = 1, 2, \cdots, n)$のもとでf(x)が最小となるxは、変数$\lambda \geq 0 (i = 1, 2, \cdots, n)$を用いて新たに定義したラグランジュ関数を満たす
- 双対問題
- SVMのソフトマージンの式にラグランジュ未定乗数法を適用し、双対問題の式を導出する
カーネルトリック
- 元の特徴空間では線形分離不可能な時、SVMは上手く動作しないことがある。そこで、特徴量をより高次元の空間に写像することで、線形分離を可能にするアプローチを考える。特徴量に対する変換関数を$\phi(x)$とした時、目的変数yを表現するモデルは$ y = w^T \phi(x) + b $と書くことができる。
この場合、写像先の空間が高次元であるほどパラメータの数が増えてしまう。そこで、問題設定を工夫することでパラメータを減らし、データ間の内積を用いて目的変数を表現するモデルを構成することができる。その代わり、写像先の空間が高次元であるほど写像したデータ同士の内積計算$\phi(x)T \phi(x')$に計算コストを要してしまう。だが実は、関数$\phi$によっては、写像先の空間における内積$\phi(x)T \phi(x')$を元の空間における関数 k(x, x') の計算によって得ることができる。これをカーネルトリックと呼ぶ。関数 k(x, x') には、動径基底関数$ k(x, x') = exp \Bigl( - \frac{|| x - x' ||^2}{\beta} \Bigr)$などがよく用いられる。
演習結果と考察
skl_regression
- 外挿問題により使用しない方がいい特徴量があることが確認できた。
- 課題
- 部屋数が ４ で犯罪率が 0.3 の物件はいくらになるか？
4240.08ドル
skl_logistic_regression
- sk_learnなど用いると便利だが、裏でどういう処理が行われているか（モデルの初期値など）を把握することが重要だと認識した
- 課題
- 年齢が30歳で男の乗客は生き残れるか？
演習コード内
model3予測結果により、
Survived==0 : 生き残れる
skl_pca
- 次元圧縮を行うとある程度決定境界が曖昧になるが、可視化できるメリットがある
- 課題
- 32次元のデータを2次元上に次元圧縮した際に、うまく判別できるかを確認
演習コード参照