1QBitのフラグメント分子軌道法論文まとめ

はじめまして。株式会社QunaSysの楊です。
QunaSysでは量子コンピュータを量子化学や物性計算に活かすことを１つのターゲットとしています。
その中で読んだ論文や実装をQiitaでまとめて行こうと思います。
（量子コンピュータに関する非技術的は話はQmedia参照 ）

最初に紹介する論文は、1QBitというカナダの量子コンピュータ向けソフトウェア会社が発表した論文です。
この論文は、古典コンピュータの計算パワーがまだまだ足りなかった20年ほど前に、非力な古典コンピュータで量子化学計算をする工夫がベースになっています。
その工夫をqubit数が少ない量子コンピュータに応用したstraightforwardな論文だと思います。

またこの論文は日経XTECHで、弊社CTO御手洗の量子回路学習と一緒に取り上げられました。
https://tech.nikkeibp.co.jp/atcl/nxt/column/18/00419/083100004/

論文のタイトルとURL

Towards the Practical Application of Near-Term Quantum Computers in Quantum Chemistry Simulations: A Problem Decomposition Approach
https://arxiv.org/pdf/1806.01305.pdf

著者

Takeshi Yamazaki, Shunji Matsuura, Ali Narimani, Anushervon Saidmuradov, and Arman Zaribafiyan
日本人の方がいっぱい！

ポイントは？

Problem Decomposition （PD） technique で大きい分子をsubsystemに分解して、それぞれのsubsystemで量子アルゴリズム（今回は基底エネルギーを計算するVQE）を動かす。subsystem同士の辻褄が合うように計算を繰り返す。
PD techniqueはfragment molecular-orbital (FMO), divide-and-conquer (DC), density matrix embedding theory (DMET) を使った。

最初2つの手法を使う場合、アルカンの計算をするのに100qubit以上の量子コンピュータが必要だが、DMETは50~100qubitでアルカンのモデリングが可能そう。

先行研究と比べて何がすごい？

今回の手法は他の量子回路の深さを削減する手法と組み合わせることが可能。
他のPD techniqueには、elongation method, molecular fractionation with conjugate caps approach, generalized X-Pol theoryなどがある。

技術の手法や肝は？

特に量子コンピュータに載せるための工夫はなさそう
。

PDによって分子を分割して、VQE（将来的にはPEA）で基底エネルギーを求める。VQEの結果を統合して、ハミルトニアンを更新してサブシステムのエネルギーを再度求めることを繰り返す。

(図は論文から抜粋) 　　

このアイデアは上手く行く？

PDの手法適用の有無による

• Qubit数削減数
  全体系にCCSDを適用して求めたエネルギーとPDの手法も用いて計算したエネルギーの
• 平均絶対偏差（mean absolute deviation (MAD)）
• 相関係数（Pearson correlation coefficient (ρ_P)）
• スピアマンの順位相関係数（Spearman’s rank correlation coefficient (ρ_S)）
  を評価した。

計算の対象は直鎖のアルカン（C_nH_2n+2）で、
1フラグメントは炭素原子１つと水素原子2つで、鎖の両端の場合は水素原子３つ。

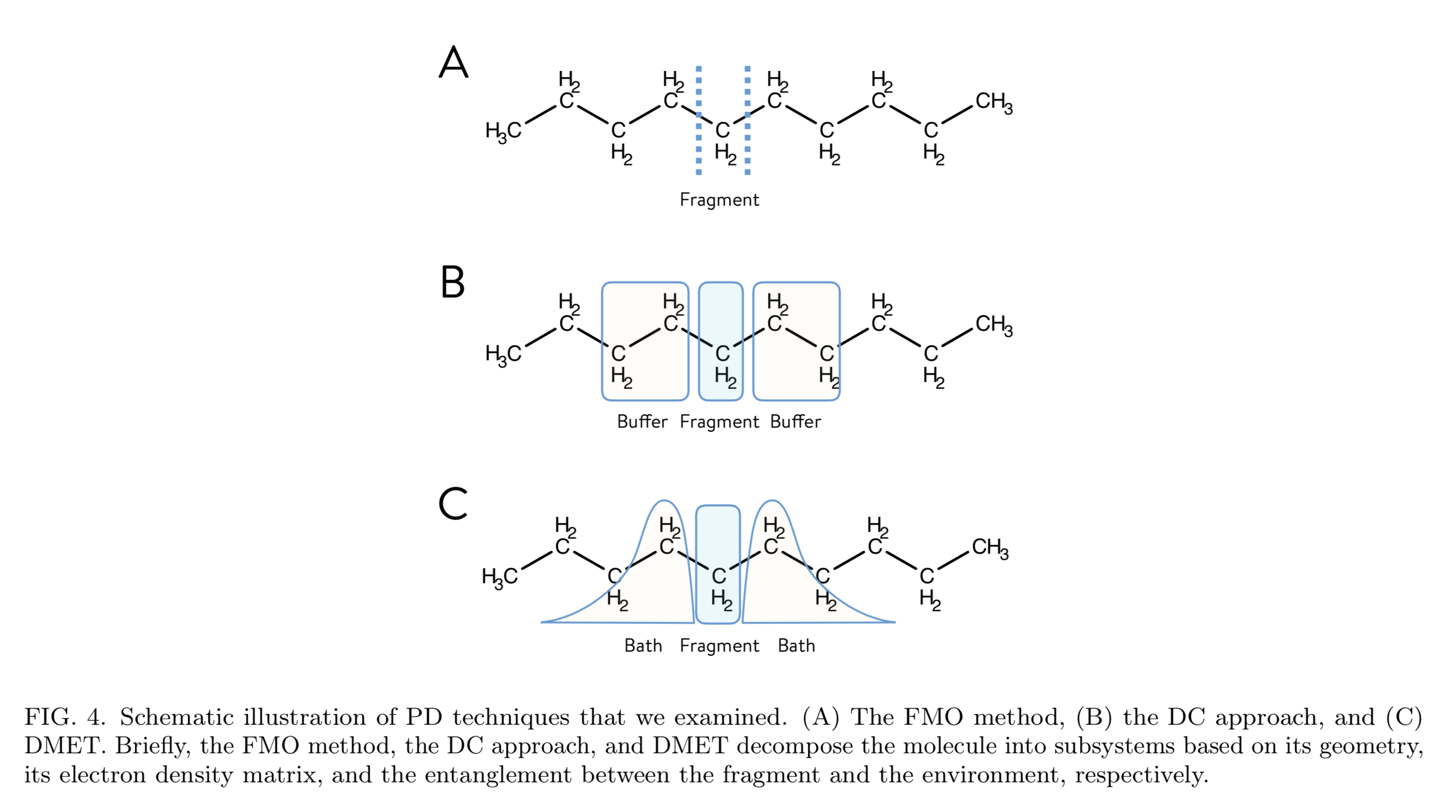(図は論文から抜粋)

実験内容と結果（一例）は以下の通り。

下の図はオクタンの52異性体のそれぞれの全体系にCCSDを使って求めたエネルギーと各PDの手法で求めたエネルギーのプロット。
全ての点で縦軸と横軸の値が一致するとρ_P=1,ρ_S=1になり、そうなるのが理想的。
表のA, B, CはそれぞれFMO, DC, DMETに対応。基底は6-31G。

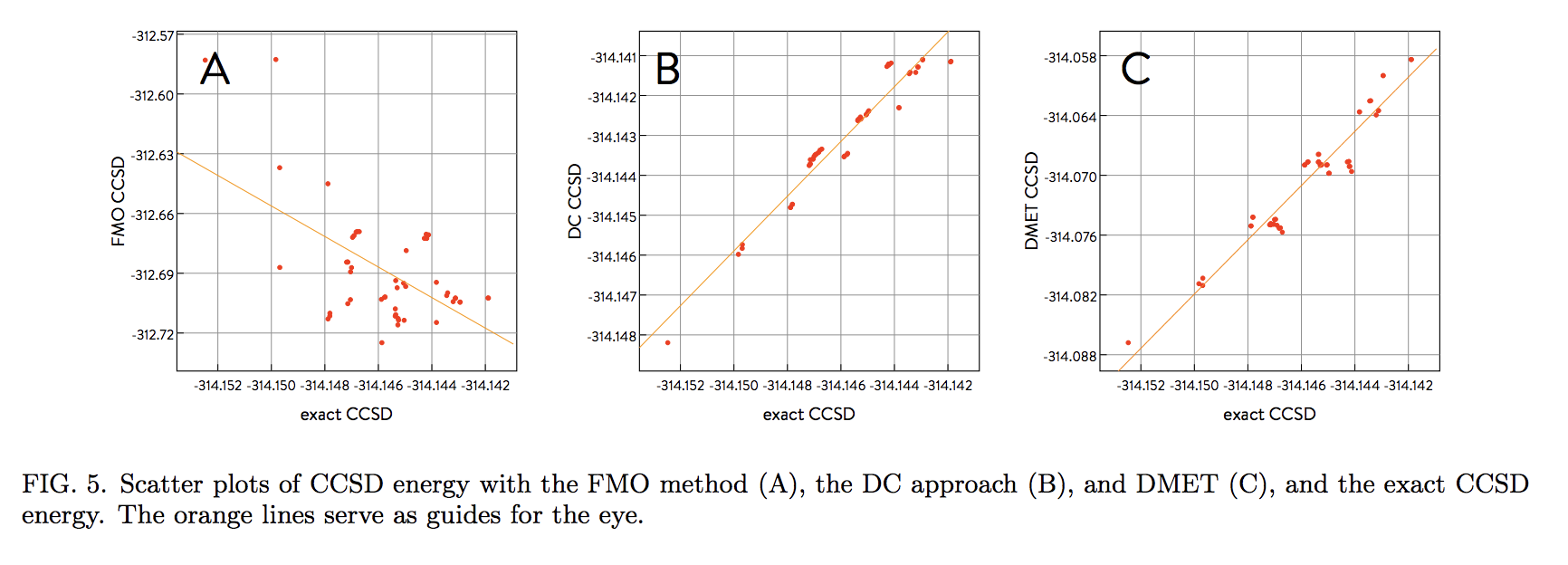(図は論文から抜粋) 　　

考察は以下の通り。
FMO: 精度は全く出ないがqubit数を70%削減できた。基底の数が多い基底関数を利用するか、1フラグメントを炭素2つにすると精度が上がる。（ただし、その場合qubit数の削減幅は小さくなる）
DC: 高精度にエネルギーが求まるが、qubit数が大して削減されない。これはbufferを4Åと大きくしたことによる。分子量が増え、bufferが相対的に小さくなれば有用な手法だと考えられる。
DMET: 精度が良く、 qubit数を80%削減。

議論はある？

NISQデバイスで重要になるサンプリングエラーによる計算精度の影響を調べた。サンプリングエラーの標準偏差が0.005 hartreesあると、ρ_P が0.96 から 0.74 に ρ_S が 0.86 に 0.70落ちる。

結構エラーにセンシティブ。

関連文献

• 最適化を分割して解いている論文 https://arxiv.org/pdf/1708.03439.pdf

• FMOの元論文 https://www.sciencedirect.com/science/article/abs/pii/S000926149900874X
• DCの元論文 https://link.springer.com/chapter/10.1007/978-90-481-2853-2_5
• DMETの元論文 https://arxiv.org/pdf/1610.06910.pdf

実装して次回に回します。