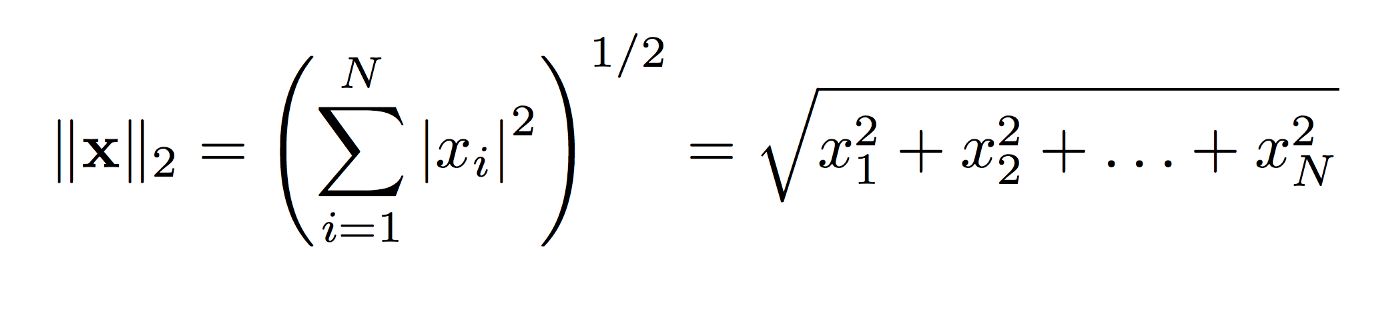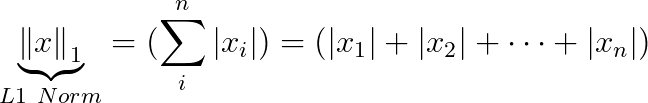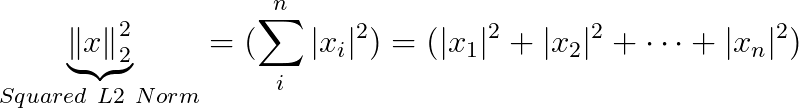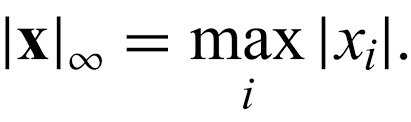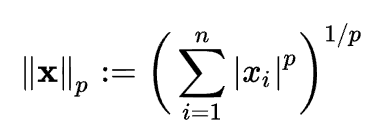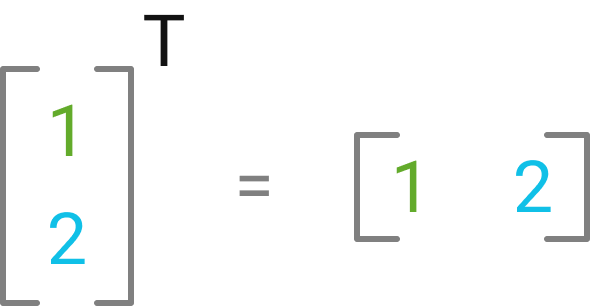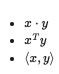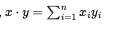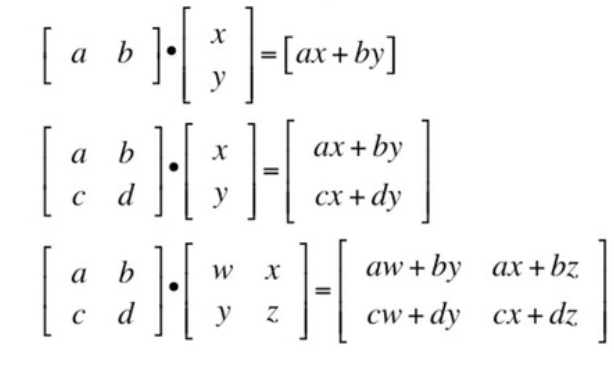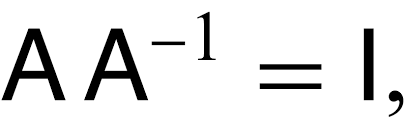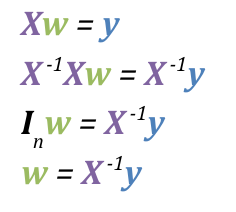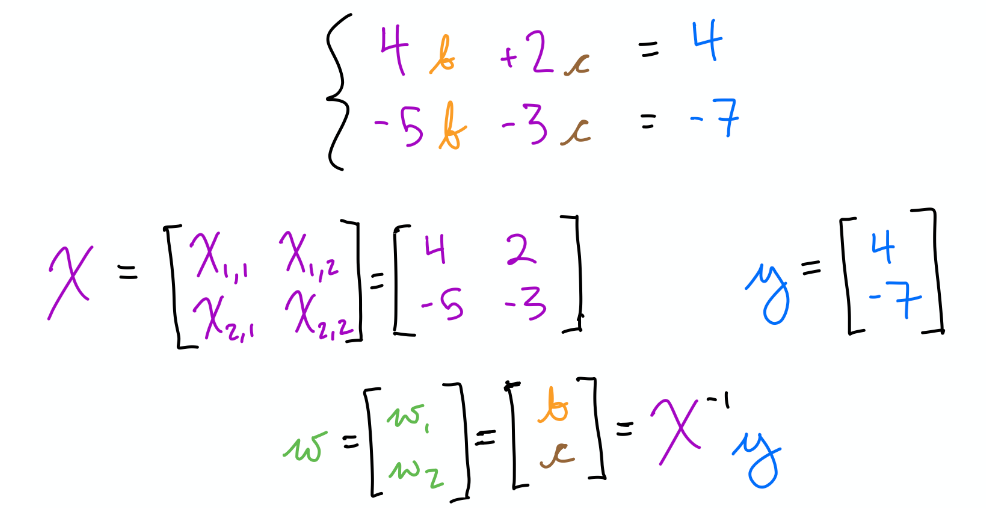ML Math
- Linear Algebra Data Structures
- Tensor Operations
- Matrix Properties
- Eigenvectors and Eigenvalues
- Matrix Operations for Machine Learning
- Limits
- Derivative and Differentiation
- Automatic Differentiation
- Partial-Derivative Calculus
- Integral Calculus
- Reference
Linear Algebra Data Structures
| Dimensions | Mathematical Name | Description |
|---|---|---|
| 0 | scalar | magnitude only |
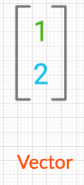
| 1 | vector | array |
| 2 | matrix | flat table, e.g., square |
| 3 | 3-tensor | 3D tables, e.g., cube |
| n | n-tensor | higher dimensional |
| Scalars | Vectors | Matrices | Tensors |
|---|---|---|---|
| No-D | 1D | 2D | 3D |
| x | x | X | . |
 |
 |
 |
. |
 |
 |
 |
 |
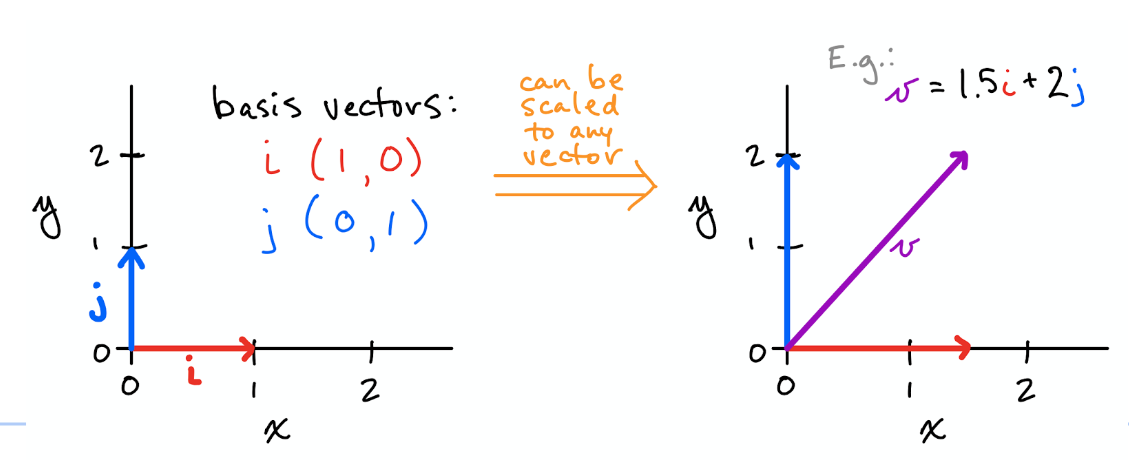| - | Vector of Length n represents location in n dimensional space | (n_row, n_col) e.g., x[0:2], 0:2]
|
. |
NORM
- Normalization helps you to scale down your features between 0 to 1
- Norms are used to express distances, e.g., this vector and this vector are this far apart, according to this norm.
- If you use l2-normalization, “UNIT NORM” means that if we squared each element in the vector, and summed them, it would equal 1.
| L^2 | L^1 | Squared L^2 | Max Norm (L∞) | Generalized L^p Norm |
|---|---|---|---|---|
 |
 |
 |
 |
 |
| measure simple (Euclidean) distance from origin | taxi cab distance | Computationally cheap but grows slowly near origin (not good for distinguishing 0 and non 0) | For every feature, the minimum value of that feature gets transformed into a 0, the maximum value gets transformed into a 1, and every other value gets transformed into a decimal between 0 and 1 | 1<= p, where p ∈ real number |
| requires x vector for derivative of element x | requires its element alone for derivative of element x, i.e., (L^2)^2 == X T X | |||
(25**2 + 2**2 + 5**2)**(1/2) |
(25**2 + 2**2 + 5**2) |
|||
np.linalg.norm(x) |
np.abs(25) + np.abs(2) + np.abs(5) |
np.dot(x,x) |
np.max([np.abs(25),np.abs(2),np.abs(5)]) |
- Robustness: L1 > L2
- Stability: L2 > L1
- Solution numeracy: L2 one, L1 many
- ※Vector has magnitude and direction
-
Unit Vectors
- A unit vector is a vector with magnitude of 1
- known as a direction vector
- notation: a lowercase letter with a cap ('^') symbol
Vector Transposition
-
x = np.array([[1,2,3]]) // NESTED matrix-style (transposing a 1D has NO effect) x_t = x.T
Orthogonal Vectors
- x and y are orthogonal vectors if xTy = 0
- x and y are at 90 degrees angle to each other
- n-dimensional space has max n mutually orthogonal vectors
-
Basic vectors are orthogonal
-
i = np.array([1,0]) j = np.array([0,1]) np.dot(i,j) //output: 0
-
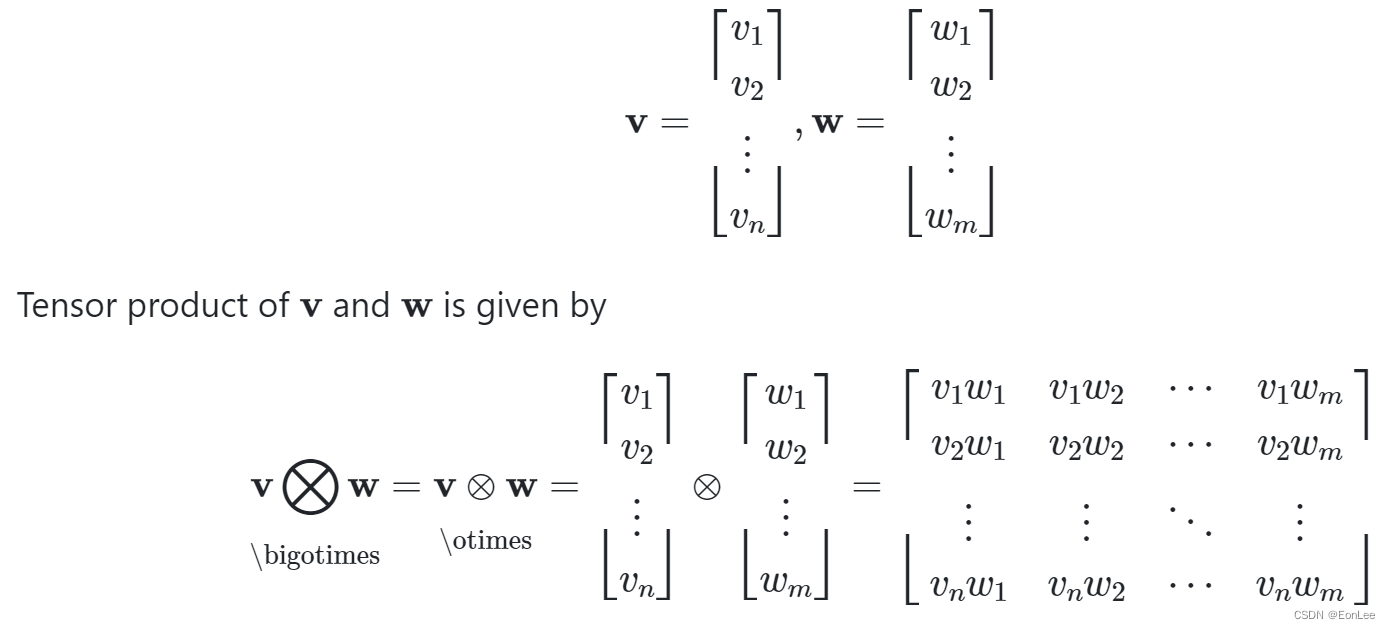
Tensor Operations
※Tensor = Scalar or Vector
-
HADAMARD PRODUCT = ELEMENT-WISE PRODUCT:
-
DOT PRODUCT
Matrix Properties
-
FROBENIUS NORM
- Frobenius norm of a matrix is equal to L2 norm of singular values
X = np.array([[1, 2], [3, 4]]) //numpy (1**2 + 2**2 + 3**2 + 4**2)**(1/2) np.linalg.norm(X) #same function as for vector L2 norm //pytorch X_pt = torch.tensor([[1, 2], [3, 4.]]) # torch.norm() supports floats only torch.norm(X_pt)
- Matrix DOT PRODUCT
- MATRIX INVERSION
-
->The inverse of matrix is used of find the solution of linear equations through the matrix inversion method.
-
e.g., we can find parameters values using matrix inverse below:
then,
-
matrix inversion is NOT possible when:
-
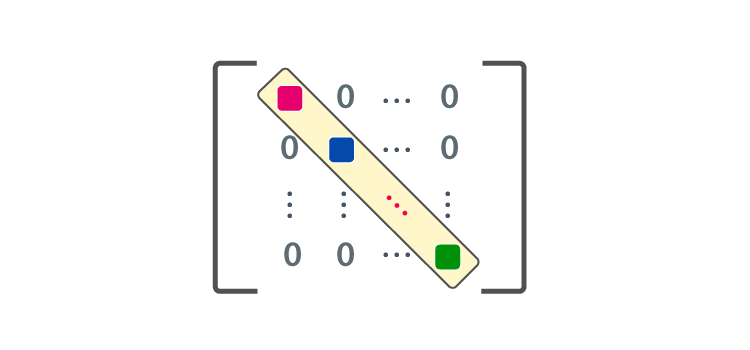
- DIAGONAL MATRIX : diag(x)
- A square matrix in which every element except the principal diagonal elements is zero
- Multiplication: diag(x)y = x ⊙ y : efficient!
- Inversion: diag(x)-1 = diag[1/x1, … , 1/xn]T
- ORTHOGONAL MATRIX
- ->Calculating A_transpose is cheap, so if the matrix is orthogonal, use A_inverse!
- SYMMETRIC MATRIX
Eigenvectors and Eigenvalues
-
3 options in linear algebra: one, no, or infinite solutions.
-
"Eigenvector of a matrix A is a vector represented by a matrix X such that when X is multiplied with matrix A, then the direction of the resultant matrix remains the same as vector X. Mathematically, the above statement can be represented as AX = λX"
-
NumPy eig() method: returns a tuple of a vector of eigenvalues and a matrix of eigenvectors
A = np.array([[-1, 4], [2, -2]])
# cheat with NumPy eig() method using eig() which returns touples
Vector_eigenvalues, Matrix_eigenVectors = np.linalg.eig(A)
#Vector_eigenvaluesas: a vector of eigenvalues
#Matrix_eigenVectors: a matrix of eigenvectors
Determinant
Determinants & Eigenvalues
- det(X) = product of all eigenvalues of X
Matrix Decomposition
-
->
- ※in order to reconstitute the original matrix
- Matrix decomposition are mostly used to solve linear systems in a easy way or quickly.
-
Common decomposition methods
-
Eigenvalue-based decomposition
- mostly applicable to square matrices
- matrix decomposes into 3 parts: final rotation, scaling, initial rotation
- "Matrix factorization reduces a computer's storage space for matrices, instead of storing the large non-factorized matrix(A), We can use less storage for its factors, sometimes even smaller when the rank of a matrix is small."
-
Singular Value Decomposition (SVD)
- SVD is a factorization of that matrix into three matrices: U, S, V.
- U: left singular valued matrix
- S: sigular valued matrix
- V: right singular valued matrix.
- U,V are orthogonal matrices
- SVD is a factorization of that matrix into three matrices: U, S, V.
-
Matrix Operations for Machine Learning
Limits
Derivative and Differentiation
Automatic Differentiation
Partial-Derivative Calculus
Integral Calculus
Reference
- https://www.citycollegiate.com/vectorXa.htm
- https://www.w3schools.com/ai/img_tensor.jpg
- https://miro.medium.com/max/1180/1*XmWq6hUA6-FanhFICmMZFg.png
- https://speakerdeck.com/tanimutomo/before-we-begin-the-mathematical-building-blocks-of-neural-networks?slide=39
- https://www.quora.com/How-can-I-calculate-the-inverse-of-a-diagonal-matrix
- https://www.geeksforgeeks.org/how-to-calculate-the-unit-vector/
- https://byjus.com/questions/what-is-unit-vector-in-physics/
- https://www.geeksforgeeks.org/eigen-values-and-eigen-vectors/
- https://medium.com/analytics-vidhya/understanding-of-matrix-factorization-mf-and-singular-value-decomposition-svd-1a38c2d5bbaa