ニューラルネットワークの重みにベイズを突っ込んでみよう
この頃増えてきている確率的なニューラルネットワークとは何だろうということで、調べてみた。
TensorFlow Probabilityで簡単に実装できるようになったので、これから流行るだろうし。
ライブラリの元論文。
Edward: A library for probabilistic modeling, inference, and criticism
そもそも、ニューラルネットワークはいろいろと便利だけど、やたらと自信満々という問題がある。
SoftMaxは、自信を語ってるわけでもないので、知らないデータでも、必ず何か元気よく答えるし。
データが大量にあって、外れ値がない場合は良いけれど、実データ使うとそうも言えない。医療データとか、特に。
例えば、車載向けにSemantic setgmentationをした場合、データを増やせば何とかなる(Epistemic uncertainty)なのか、そもそも問題がそういうもんで、データ増やしてもどうにもならない(Aleatoric uncertainty)か、わけて考えたい。
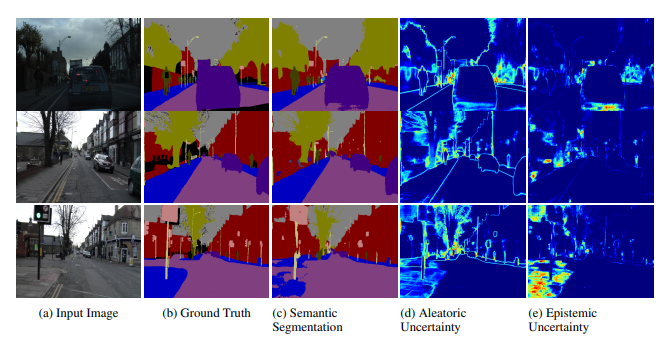
What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?(NIPS2017)
この例でわかるように、データを増やしたところでSemantic setgmentationのボーダーの部分はどうこう出来るモノでもない。
で、こういう、もやっとしたデータ処理と言えば、ベイズだろうということで、この頃確率的なニューラルネットワークというのが増えている。
基本的に、ニューラルネットワークの重みとかActivationを確率にして、そのDistributionを求めることになる。
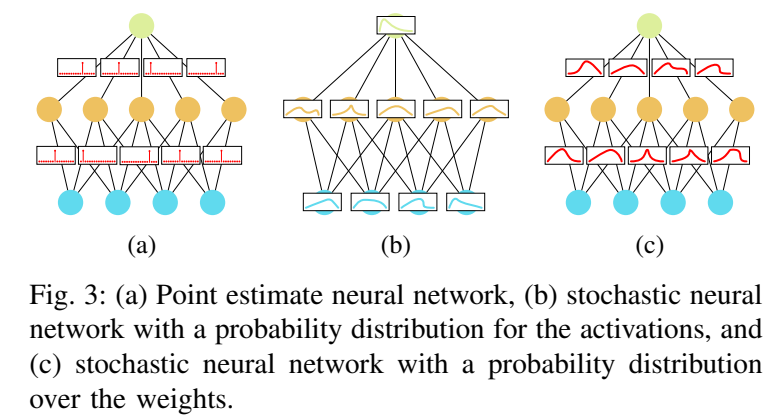
いつものが、左で、真ん中がActivationに確率突っ込んだので、右が重みに確率付き。
この確率の導き出し方は、ベイズの歴史を紐解くわけで、いっぱいある。
MCMCを使うのから、画像生成なんかで大活躍しているVariational Inferenceを使ったのまで。
この中から今回はBayes by Backpropというのを、紹介する。これが出てから、大規模なネットワークにも適用できるようになって、リバイバルの元になっている模様。(とはいえ、Dropoutも結局ベイズだからとか言い出すと、みんな普通にいつも使っていたとも。)
いろいろある手法の全体像は、こちらのSurveyがわかりやすい。上の図もこっから。
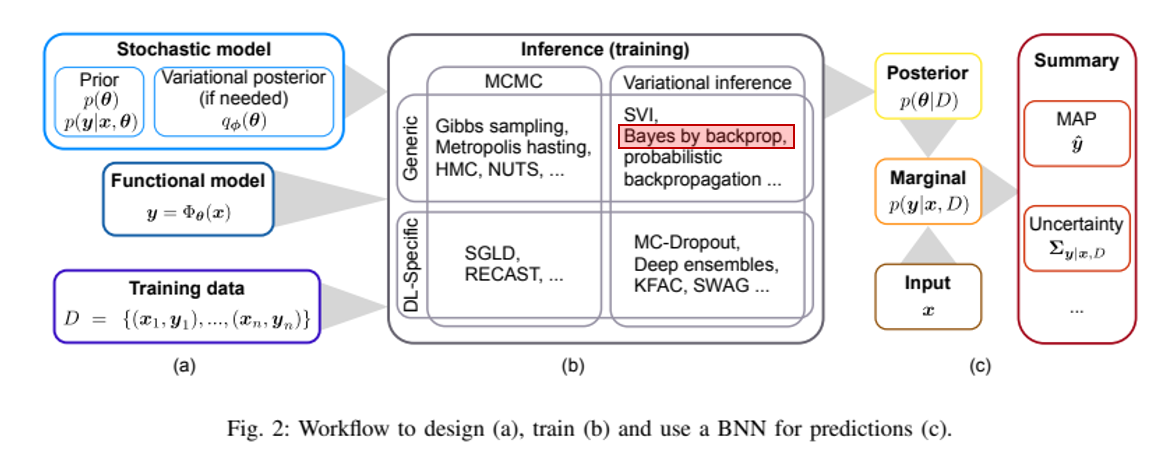
Hands-on Bayesian Neural Networks – A Tutorial for Deep Learning Users(2022年)
Bayes by backprop
Variational Inferenceを用いる手法で、重みをGaussianに近似して、Reparameterization trickを使ってGaussianのアップデートをBackpropagationで行う手法らしい。
今回は、最初の論文を追いかけてみる。
Weight Uncertainty in Neural Networks(ICML2015)
ベイズは今までの積み上げがすごくて、これを今から追いかけるとかなり大変なので、必要最低限のところから見ていく。
まずは、学習データを$D= (x_i, y_i)$、重みを$w$とする。
そうすると、いつものPoint estimate手法でLossを計算すると、最尤推定だと
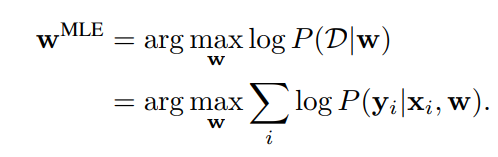
最大事後確率だと
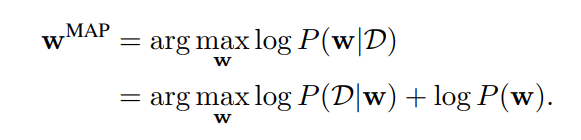
この時、$w$がGaussian priorの場合はL2 regularization (weight decay)、Laplace priorの場合はL1 regularizationになる。
ここで、重みに、確率分布を当てはめて、もっとモヤっとさせる。
新しいデータ$(\hat{x_i}, \hat{y_i})$が来た時、$\hat{y_i}$の確率は以下で計算する。

近似するので、出来るだけこの近似は元のと同じようになって欲しいので、KL-divergenceを最小化させる。
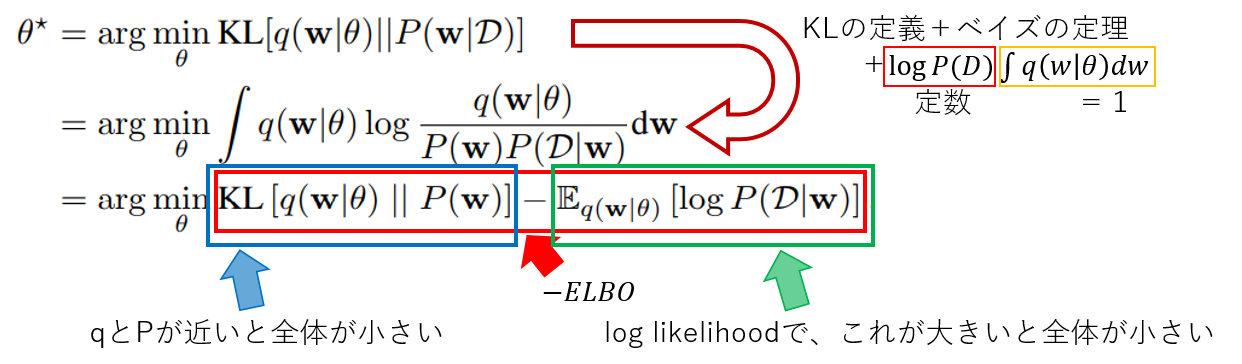
この頃人気の画像生成系ネットワークで良くみるvariational free enerygyとかELBOとか言われるものが導き出された。
右側の期待値は、$q$の分布が全て元のMLEにくるようにすれば、大きくできる。
これを更に変形すると
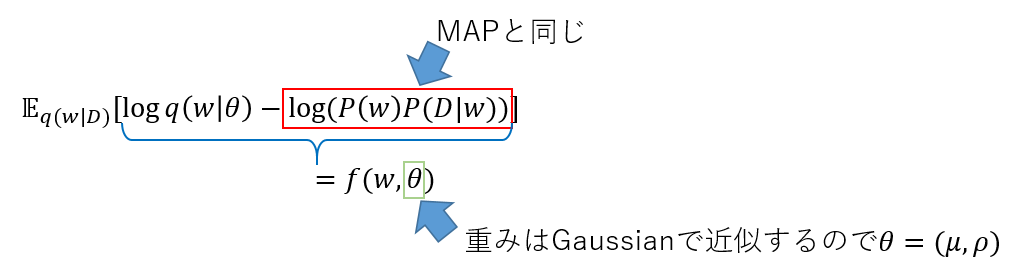
この新しいLoss関数$f$を最小化すれば良くなった。
期待値の中で微分をしたいので、reparameterization trickを使う。まだ、新しい分野ということで、表記ゆれが激しく、pathwise derivative estimator, infinitesimal perturbation analysis, stochastic backpropagationなんかとも呼ぶらしい。
まず$w$をGaussianで近似する。この際、分散は正にしたいので、以下の形にする。

これにより、
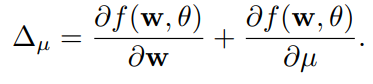
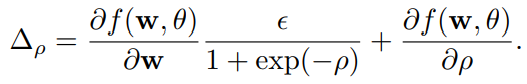
の計算が出来て、普通にBackpropagationが使える。
これで、重みのパラメーターは2倍になっているけど、ネットワークの自信のなさは説明がつく。
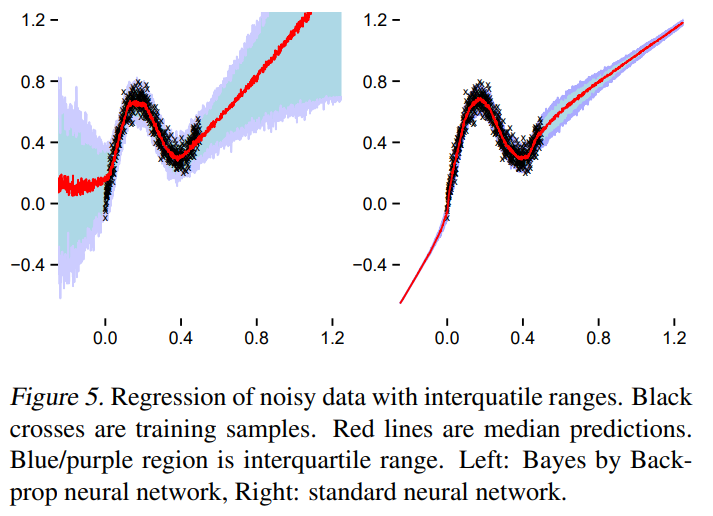
左が、Bayes by Backpropで右がいつものNeural Network。
データがないところで、Inferenceをすると違いが良くわかる。
導出の部分は、VAEの有名論文に詳しい。
Auto-Encoding Variational Bayes
この重みをGaussianではなくBernoulliで近似するとGaussianと違って、パラメータ数は増えなくDropoutと同義になるらしい。
Bayesian Convolutional Neural Networks with Bernoulli Approximate Variational Inference
Bayes by BackpropをConvに当てはめている論文もあり
Uncertainty Estimations by Softplus normalization in Bayesian Convolutional Neural Networks with Variational Inference
Variance Networks: When Expectation Does Not Meet Your Expectations
これから、流行るのではなかろうか。