JModelicaで常微分方程式初期値問題を解く

#目的・狙い

• 流行りの1DCAEを使いたい
• JModelicaのinterfaceの使い勝手を確認したい
• Modelica言語を勉強する
• OpenModelicaでいいのではと言われる前にJModelicaのいいところを探したい

尚、環境構築方法はJModelicaをUbuntuにインストールするの記事を参照。

#JModelicaの基本的な使い方

1. Modelファイル(*.mo)を用意する
2. Function Mockup Units(以下FMUs)にコンパイル
3. FMUsを読み込む
4. 読み込んだFMUsを計算する
5. 結果を見る

もちろん、３の工程からコンパイル済みのFMUsを読み込むことも可能。

---

#常微分方程式を解く
Google先生によるとModelicaでHelloWorldと言えば、1階の線形常微分方程式の初期値問題が多いようである。

\begin{eqnarray}
\frac{dx(t)}{dt} &=& -x(t) \\
  x(0) & = & 1
\end{eqnarray}

紙と鉛筆で解く方法は教科書に任せて、解析解の導出はSymPyで行う。SymPyを利用できる環境下で下記を実行。

python

import sympy
x = sympy.Function("x"); t,C1 = sympy.symbols("t C1")
#x(t)について解く x(t) == C1*exp(-t)
ans = sympy.dsolve(x(t).diff(t)+x(t),x(t))
#積分定数C1を計算(t=0,x(0)=1)し、ansの式に代入する
C = {C1:ans.subs(x(t),1).subs(t,0).lhs}
ans.subs(C)
#--> x(t) == exp(-t)

以上から解析解は以下のようになる。

\begin{eqnarray}
  x(t) & = & \exp(-t)
\end{eqnarray}

---

#JModelicaで常微分方程式を解く
##1.モデルファイルの準備
以下のモデルファイルを準備する

ode_test.mo

model HelloWorld 
	Real x(start=1);
equation
	der(x)= -x;
end HelloWorld;

1行目～５行目：モデル（クラス）定義
２行目：初期値1の状態変数xの定義
３行目：各変数の関係式を以下で定義するよ。の合図
４行目：dx/dt = -x　の方程式を定義

---

##2.モデルをFMUsにコンパイル
モデルファイルのディレクトリでJModelicaを起動。(インストール場所は適宜変更）

bash

/home/ubuntu/JModelica/bin/jm_ipython.sh

ipython

from pymodelica import compile_fmu
hello_fmu = compile_fmu("HelloWorld","./ode_test.mo")

##3. FMUsを読み込む

ipython

from pyfmi import load_fmu
hello_model = load_fmu(hello_fmu)

---

##4. 読み込んだFMUsを計算する
1秒分計算する

ipython

res = hello_model.simulate(final_time=1)

##5.結果を見る
状態変数xの結果はres["x"]でアクセスできる。
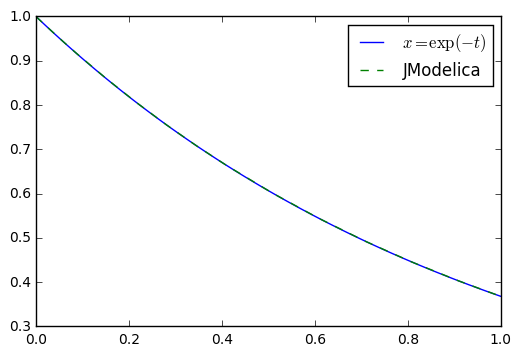
先の解析解を合わせてグラフ化する。

ipython

import numpy as np
from matplotlib import pyplot as plt
t = np.linspace(0,1,101)
x = np.exp(-t) 
plt.plot(t, x, label="$x=e^(-t)$")
plt.plot(res["time"],res["x"],"--",label="JModelica")
plt.legend()
plt.show()

---

---

#Assimuloで常微分方程式を解く

Assimuloって

• JModelicaの積分器を担うPythonのモジュール(JModelicaが使える環境であれば使える)
• 常微分方程式を解くのに便利
• Anacondaな人はconda install -c https://conda.binstar.org/chria assimuloでインストール

ipython

from assimulo.solvers import CVode
from assimulo.problem import Explicit_Problem
#微分方程式を表す関数を定義
def ode_func(t,x):
    dxdt = -x[0]
    return np.array([dxdt])
#陽的な問題と積分器を含んだモデルを定義し計算
exp_mod = Explicit_Problem(ode_func, 1) #xの初期値は1
exp_sim = CVode(exp_mod)
t1, x1 = exp_sim.simulate(1)#計算時間1秒
#結果のプロット
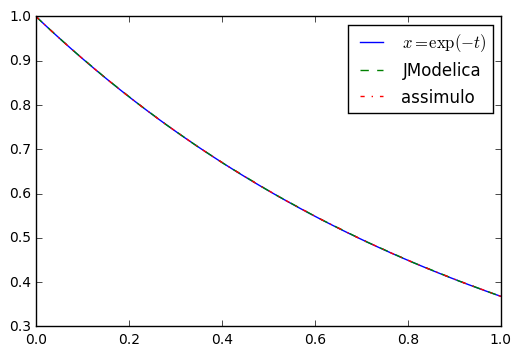
plt.plot(t, x, label="$x=\exp(-t)$")#先に計算した解析解
plt.plot(res["time"],res["x"],'--',label="JModelica")#JModelicaの数値解
plt.plot(t1,x1,'-.',label="assimulo")#Assimuloの数値解
plt.legend()
plt.show()

---

---

#まとめ

• 1階の線形常微分方程式初期値問題の解析解をSymPyで導出した
• JModelicaの基本的な使用方法を確認した
  • 計算結果(数値解)の見た目は解析解と比較して良好
  • 計算結果をPythonで扱えるので便利
• Assimuloで常微分方程式を数値的に解いた
  • 常微分方程式が立てられているのであれば便利
• Assimuloの読み方が不明