1. 人口動態のベイズ推定ー国連モデル
一般的に、人口動態推定は、合計特殊出生率(TFR)の評価、及び平均寿命の評価の2つの評価に分けられる。なお、人口動態推定は人口動態転換モデルを用いて記述されており、一般的に、人口動態転換モデルは4段階から構成される。第一段階では、出生率・死亡率ともに高レベルにある状況が想定されており、第二段階では、出生率は高レベルにあるが、死亡率が急速に減少する過程が想定されている。第三段階では、出生率が減少、死亡率は徐々に減少する過程を想定している。また、第四段階では、出生率・死亡率ともに低レベルにある状況が想定されている。
国連では、現在、階層ベイズモデルを用いて人口動態推定を行なっており、ここでは国連モデルに基づいた評価を実行する。
1.1 TFRのベイズ推定
国連モデルでは、まず、人口動態転換モデルの第二段階におけるTFRの推移は二重ロジスティック関数をドリフト項に持つランダム・ウォークに従うものとする。
f_{t+1} = f_{t} - g(f_t\mid \vec{\delta}) + \epsilon_t
ここで、ドリフト項は以下で与えられるものとする:
g(f_t\mid \vec{\delta}) =
\frac{-d}{1+\exp\left[- \frac{2 \ln(9)}{\nabla_1}
\left( f_t - \sum_{i=2}^{4}\nabla_i + 0.5 \nabla_1 \right) \right]}
\\\
+
\frac{d}{1+\exp\left[- \frac{2 \ln(9)}{\nabla_3}
\left( f_t - \nabla_4 - 0.5 \nabla_3 \right) \right]}
ここで、$\vec{\delta} = (\nabla_1, \nabla_2, \nabla_3, \nabla_4, d)$ はモデルのパラメータであり、誤差項は一般に時間依存するものとする:
\epsilon_t \sim \mathcal{N}(0, \sigma_t^2) \, , ~
\sigma_t = \sigma(f_t)
ベイズ推定モデルでは、初めに、データの平均値 $\mu$、及びパラメータの分散 $\sigma_t$ を元にして推定されるパラメータの事前分布を与える必要があり、パラメータの事後分布は、マルコフ連鎖モンテカルロ(MCMC)シミュレーションを用いて推定することができる。
人口動態転換モデルの第三段階におけるTFRの推移は、TFRの漸近的な値 $\mu$ 周りの揺らぎとして、AR(1)モデルによってモデル化される:
f_{t+1} - \mu = \rho \left( f_t -\mu \right) + \epsilon_t
ここで、$\epsilon_t \sim \mathcal{N}(0, \sigma_t^2),~0 \leq \rho \leq 1$ を満たすものとする。
1.2 平均寿命のベイズ推定
国連モデルでは、TFRと同様に、平均寿命 $\ell_t$ を推定する場合にも、ベイズ推定モデルで定式化されており、平均寿命 $\ell_t$ の推移は二重ロジスティック関数をドリフト項に持つランダム・ウォークに従うものとする。
\ell_{t+1} = \ell_{t} + g(\ell_t\mid \vec{\delta'}) + \epsilon_{t+1}
ここで、ドリフト項は以下で与えられるものとする:
g(\ell_t\mid \vec{\delta'}) =
\frac{k}{1+\exp\left[- \frac{\ln(81)}{\Delta_2}
\left( \ell_t - \Delta_1 - 0.5 \Delta_2 \right) \right]}
\\\
+
\frac{z-k}{1+\exp\left[- \frac{\ln(81)}{\Delta_4}
\left( \ell_t - \sum_{i=1}^{3} \Delta_i - 0.5 \Delta_4 \right) \right]}
ここで、$\vec{\delta'} = (\Delta_1, \Delta_2, \Delta_3, \Delta_4, k,~z)$ はモデルのパラメータであり、誤差項は一般に時間依存するものとする:
\epsilon_{t+1} \sim \mathcal{N}(0, \sigma_t^2) \, , ~
\sigma_t = \sigma(\ell_{t})
各々のパラメータは、次のように解釈することができる。第一に、パラメータ $k$ は第一段階の増加過程が定常化する値に相当しており、 パラメータ $\Delta_1$ は第一段階の増加過程の平均寿命が10%となる場合に当たり、パラメータ $\Delta_2$ は第一段階の増加過程の平均寿命が10〜90%の間の値をとる期間(年数)を表しており、パラメータ $\Delta_3$ は第一段階の増加過程の平均寿命が90%にあり、且つ二番目の定常状態が10%にある期間(年数)を表している。また、パラメータ $z-k$ は第二段階の増加過程が定常化する値に相当し、パラメータ $\Delta_4$ は二番目の定常状態における平均寿命が10〜90%の間の値をとる期間(年数)を表している。そして、パラメータ $k$ は5年間の女性の平均寿命の漸近的な増加率を表している。
2. モンテカルロ法を用いた人口動態予測
第一に、2100年までの期間を対象として、モンテカルロ法を用いて日本の合計特殊出生率(TFR)を推計する。下記に将来の推計値を図示しているが、TFRの推計値には比較的大きな誤差が含まれることが容易に見てとれる。このTFRの推計誤差が、最終的には人口動態の予測に大きな誤差を生じる要因ともなる。
library(bayesTFR)
tfdir <- './pop/TFR/sim20190525'
m2 <- get.tfr.mcmc(tfdir)
m3 <- get.tfr3.mcmc(tfdir)
pred <- get.tfr.prediction(tfdir)
tfr.trajectories.plot(pred, country = "JP", nr.traj = 50, main = "MCMC estimation of Total Fertility Rate (TFR) for Japan")
summary(pred, country = "JP")
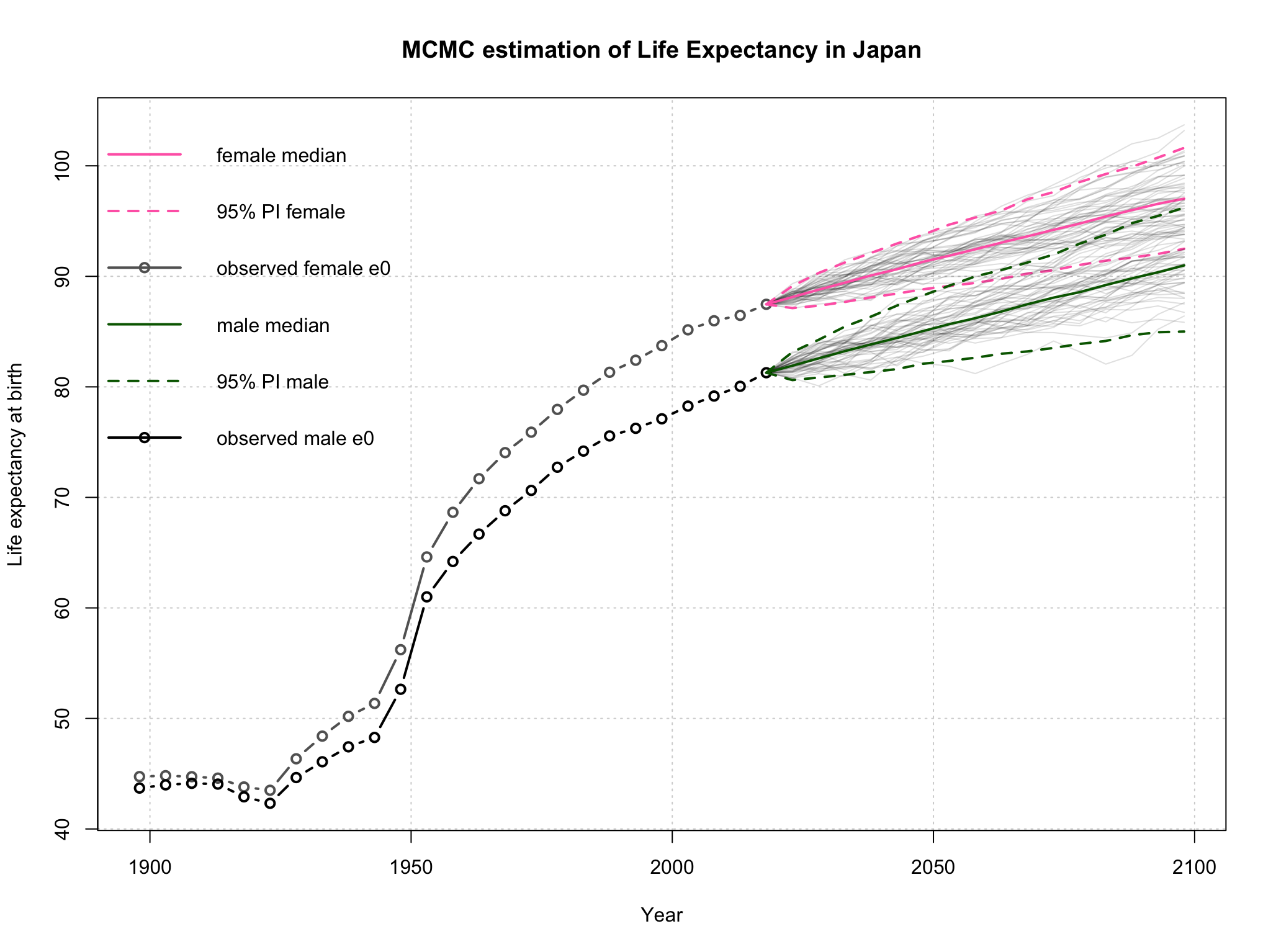
次に、モンテカルロ法を用いて日本の平均寿命を推計する。下記に将来の推計値を図示しているが、平均寿命にも比較的大きな推定誤差が含まれることが見てとれる。
library(bayesLife)
e0dir <- './pop/e0/sim20190528'
m <- get.e0.mcmc(e0dir)
pred <- get.e0.prediction(e0dir)
e0.trajectories.plot(pred, country = "JP", both.sexes = TRUE, nr.traj = 50, main = "MCMC estimation of Life Expectancy for Japan")
最後に、上記で推定した合計特殊出生率(TFR)と平均寿命の推計値を用いて、モンテカルロ法を用いた人口動態の将来予測を実行する。
library(bayesPop)
popdir <- './pop/output'
pred <- pop.predict(output.dir=popdir, verbose=TRUE, replace.output=TRUE,
inputs = list(tfr.sim.dir=tfdir,
e0F.sim.dir=e0dir, e0M.sim.dir="joint_"))
pop.trajectories.plot(pred, country = "JP", nr.traj = 50, sum.over.ages = TRUE, main = "MCMC estimation of population in Japan")
pred.pyr <- get.bPop.pyramid(pred, country = "JP", year=2050)
plot(pred.pyr, title(sub = "MCMC estimation of population for Japan in 2050"))
3. 米国国勢調査局のAPIを用いた推定
米国国勢調査局では、Web APIを通じて様々なデータを公開しており、2022年3月以降、人口動態推計における推計誤差の詳細な評価も実施している。
以下では、米国国勢調査局が公開しているWeb APIを用いて日本の年齢別人口の詳細なデータを取得し、2050年の人口動態予測を実行した。
import requests
from requests.exceptions import RequestException
import json
import datetime
import pandas as pd
import numpy as np
from tqdm import tqdm
# APIトークン(各自が申請取得したAPIトークンに差し替える)
token = 'XXXXXX'
class population:
def __init__(self, token):
self.headers = {
"Accept": "application/json",
"api_key": token
}
self.endpoint_url = 'https://api.census.gov/data/timeseries/idb/1year?get=NAME,AGE,POP'
#人口動態に関するデータ取得
def get_population_estimation(self, year):
try:
r = requests.get(
url = self.endpoint_url + '&GENC=JP' + '&YR=' + str(year) + '&SEX=1,2',
headers = self.headers,
timeout = 10
)
r.raise_for_status()
res = r.json()
df = pd.DataFrame(res)
df.rename(columns=df.iloc[0], inplace = True)
df.drop(df.index[0], inplace = True)
#headers = df.iloc[0]
#df = pd.DataFrame(df.values[1:], columns=headers)
except RequestException as e:
print(e.response.text)
return df
if __name__ == '__main__':
df = population(token=token).get_population_estimation(year=2050)
print(df)
ID NAME AGE POP GENC YR SEX
1 Japan 0 378559 JP 2050 1
2 Japan 1 384131 JP 2050 1
3 Japan 2 389907 JP 2050 1
4 Japan 3 395742 JP 2050 1
5 Japan 4 401411 JP 2050 1
.. ... ... ... ... ... ..
198 Japan 96 257751 JP 2050 2
199 Japan 97 232819 JP 2050 2
200 Japan 98 205734 JP 2050 2
201 Japan 99 180545 JP 2050 2
202 Japan 100 526300 JP 2050 2
4. 補足事項
人口動態の推定においては、「Estimate」と「Projection」を明確に区別しており、「Estimate」は過去と現在の値に対して用いるが、一方で、「Projection」は将来の人口動態トレンドを仮定した際に用いるものである。以下の米国国勢調査局の記載を参照。
5. 参照
-
Adrian E. Raftery, Hana Ševčíková (2023),
"Probabilistic population forecasting: Short to very long-term", International Journal of Forecasting, 39 (1).
https://doi.org/10.1016/j.ijforecast.2021.09.001. -
H. Castanheira, F. Pelletier, and I. Ribeiro (2017),
"A sensitivity analysis of the Bayesian framework for projecting life expectancy at birth", Technical Paper 7, United National Population Division, New York, NY.