東京都知事選挙(2020)の選挙結果でデータ分析

東京都知事選挙が行われましたね。
結果はともかく、開票結果を見ていたらデータ好きの血が疼いてしまい、勢いで簡単なデータ分析をしてしまいました！

ネット上のデータ取得からpandasでの処理、簡単なデータ解析までの流れのまとめにもなっているかと思います。

※以下は単純に個人の興味の範囲で、データ分析の練習として行ったことですので、政治的な意図や作為は全くありません。
また、使用したデータと分析結果の正確性・有意性についても保証しません。

##0. 分析の概要
####検証したい仮説

=> 「選挙結果は学歴と相関があるのか？」
かなりあけすけな感じですみません、、
（親の年収と子供の学力の相関の調査などが以前話題になっていたのを思い出しますね。）

####使ったデータ

• 市区町村別開票結果 *朝日新聞
  （csv形式のデータが見当たらなかったので上位５候補者分だけをExcelに手入力しました。正直言ってこれが一番時間がかかりました・・）
• 市区町村別大学卒業者の人数（2010年の国勢調査より。2015年の国勢調査ではこのデータが入手できなかったので、古いですがこれを使います）
• 市区町村別人口（本当は有権者人口が理想ですが、簡単のためこちらを使います。2020年のデータです）

####分析の流れ
以下の流れで処理しました。

1. データをpandasで読み込み、一つのDataFrameにまとめる
2. 市区町村別に大学卒業者の割合・人口に対する得票率を求める
3. 得票率のデータからk-means法でクラスタリング
4. 大学卒業割合を説明変数として各候補者の得票率を予測する線形回帰モデルを作成
5. 可視化

それでは、順番にみていこうと思います〜
なお、以下の処理はすべてGoogleColabNotebook上で行っています。

##1. データの読み込み
####票数データ

election.py

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

#票数データ（自作）
path = "~~~/xxxx.xlsx" #Drive内のパス名
df = pd.read_excel(path)

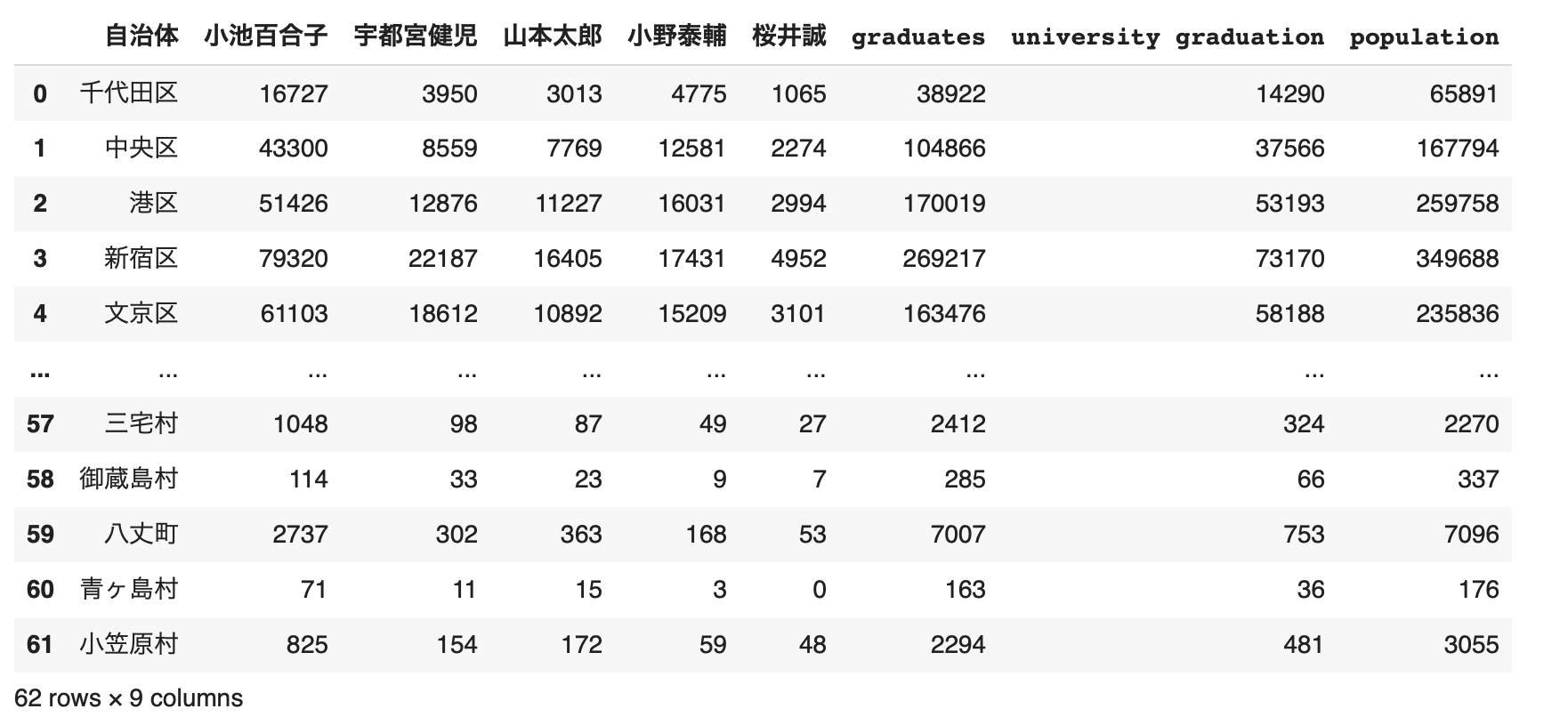
こんな感じですね。
確認はしましたが自作なので票数のミスがあってもご勘弁を・・・
（※ちなみに、選挙の開票データは前回のものならオープンデータ化されていたので、しばらくすれば今回の結果も簡単に入手できるようになるかと思います。）

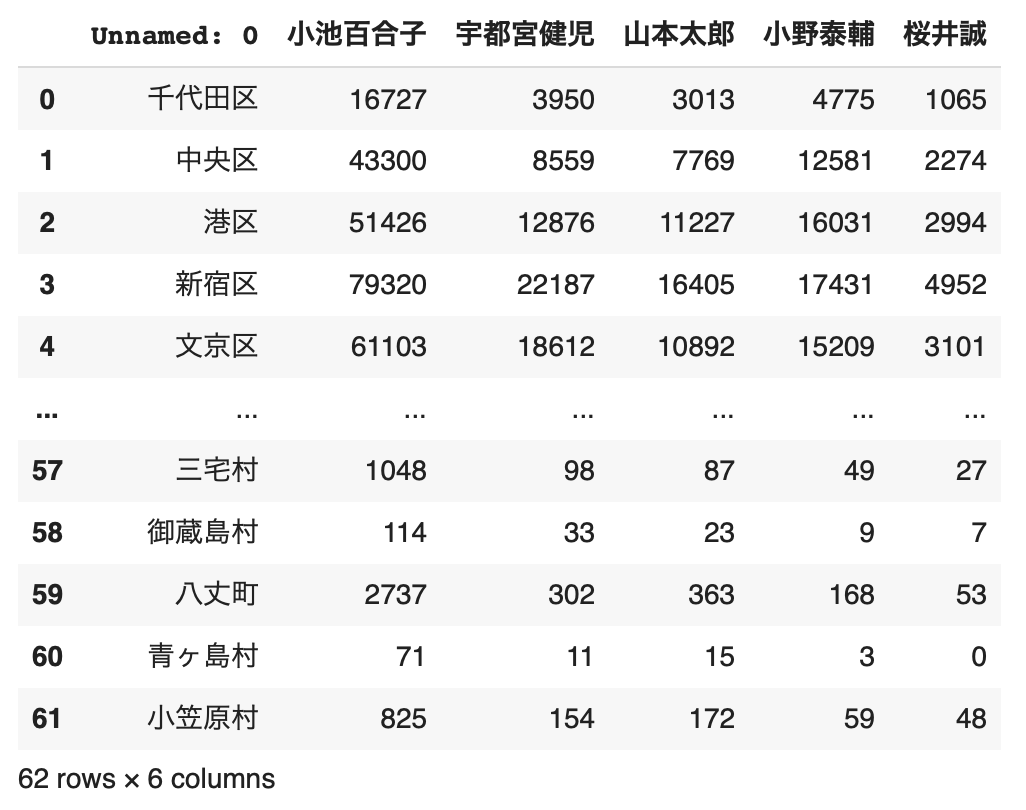
####最終学歴データ(2010)

election.py

path = "~~~/xxxx.csv" #Drive内のパス名
edu = pd.read_csv(path,encoding='cp932') #encodingは日本語入力対応用
#カラム名の行以下を抽出
edu.columns=edu.iloc[7] 
edu = edu[8:]
#市区町村の合計部分のみ取り出し
edu = edu[edu["町丁字コード"].isnull()]
#indexのリセット
edu.reset_index(inplace=True)

election.py

#卒業者人数（就学者でない人口）・大学卒業者人数（大学院含む）を結合

df2 = pd.concat([df,edu["卒業者"],edu["大学・大学院 2)"]],axis=1)
#男女別のカラム名も同じだったので重複したカラムを削除
#=>男女合計の数字のみをdf2に残す
df2 = df2.loc[:,~df2.columns.duplicated()]

ちなみに、東京都の市区町村の並びはどんな資料でも統一されているので結合は何も気にせずaxis=1でしてあげれば大丈夫です。

####人口データ(2020)

election.py

path = "https://www.toukei.metro.tokyo.lg.jp/kurasi/2020/csv/ku20rv0440.csv"
population = pd.read_csv(path,encoding='cp932')
#市区町村ごとの人口を抽出
population = population[8:]["Unnamed: 4"].reset_index()
#結合
df3 = pd.concat([df2,population],axis=1)

####データの微調整

election.py

#カラム名の変更
df3.rename(columns={"Unnamed: 0":"自治体",
        '卒業者': 'graduates', 
        '大学・大学院 2)': 'university graduation',
        "Unnamed: 4":"population"},
    inplace=True)
#不要なindex列の消去
df3.drop("index",axis=1,inplace=True)
#何故かstr型だったのでint型に変換
df3["population"] = df3["population"].astype(int)
df3["graduates"] = df3["graduates"].astype(int)
df3["university graduation"] = df3["university graduation"].astype(int)

結果、df3は以下のような感じになります。

##2. データの加工

election.py

data = df3.copy()
#得票数を人口で割って置き換え
data.iloc[:,1:6] = df3.iloc[:,1:6].values / df3["population"].values.reshape(62,1)
#大卒率のカラムを追加（大卒率＝大学卒業数/卒業数）
data["university graduation rate"] = data["university graduation"] / data["graduates"]

無事、必要なデータが揃いました。 いよいよ機械学習の出番です。

##3. k-means法でクラスタリング
sklearnを使います。

election.py

from sklearn.cluster import KMeans

kmeans = KMeans(init='random', n_clusters=3,random_state=1)

X = data.iloc[:,1:6].values #得票割合　shape=(62,5)
kmeans.fit(X)
y = kmeans.predict(X)  #クラスター番号

#クラスタリングの結果をdataに結合
data = pd.concat([data,pd.DataFrame(y,columns=["cluster"])],axis=1)

これで３クラスターに分けられたので、特徴を見てみます。
（ちなみにクラスター数（n_clusters）を変えてもやってみましたが、何となく３つぐらいが良さそうだと思ったので３にしました）

各クラスターを軸にした時のそれぞれのデータの平均を見てみます。

election.py

data.groupby("cluster").mean()

単なる平均ですが、これだけでも異なる特徴を持った集団に分けられたことが分かります。
クラスターに属する市区町村を地図で塗り分けてみましたが、

**0. 山手線内エリアとその周辺

1. 千葉県よりの区と多摩地区、一部島嶼部（御蔵島村・小笠原村）
2. 山間部と島嶼部**

という内訳でした。
得票率だけでこれだけの（常識的にみてあり得そうな）分類ができたことには驚きました。

##4. 線形回帰分析
説明変数Xは大卒の割合、目的変数Yは各候補者の得票率として線形回帰分析を行います。
以下では可視化までセットにした関数を定義しています。

election.py

from sklearn.linear_model import LinearRegression

colors=["blue","green","red"] #クラスターの色分け用

def graph_show(Jpname,name,sp=False,cluster=True,line=True):
  #Jpname: 候補者の漢字表記
  #name: 候補者のローマ字表記（グラフ用）

  X = data["university graduation rate"].values.reshape(-1,1)
  Y = data[Jpname].values.reshape(-1,1) 

  model = LinearRegression()
  model.fit(X,Y)

  print("決定係数(相関係数)：{}".format(model.score(X,Y)))
  plt.scatter(X,Y)

  #特定の自治体をグラフ中で強調（デフォルトはFalse）
  if sp:
    markup = data[data["自治体"]==sp]
    plt.scatter(markup["university graduation rate"],markup[Jpname],color="red")

  #k-meansで求めたクラスターごとに色分け
  if cluster:
    for i in range(3):
      data_ = data[data["cluster"]==i]
      X_ = data_["university graduation rate"].values.reshape(-1,1)
      Y_ = data_[Jpname].values.reshape(-1,1) 
      plt.scatter(X_,Y_,color=colors[i])
      
  #回帰直線を表示
  if line:
    plt.plot(X, model.predict(X), color = 'orange')

  plt.title(name)
  plt.xlabel('university graduation rate')
  plt.ylabel('vote')  
  plt.show()

##5. 可視化
先ほど定義したshow_graphを使って各候補者のグラフを表示させます。
（以下敬称略で失礼します）

※回帰直線は決定係数が0.5を超えたものだけ表示しています
※特定の自治体を目立たせて表示する機能はここでは使いません
※clusterの色は　０：青　１：緑　２：赤

####小池百合子

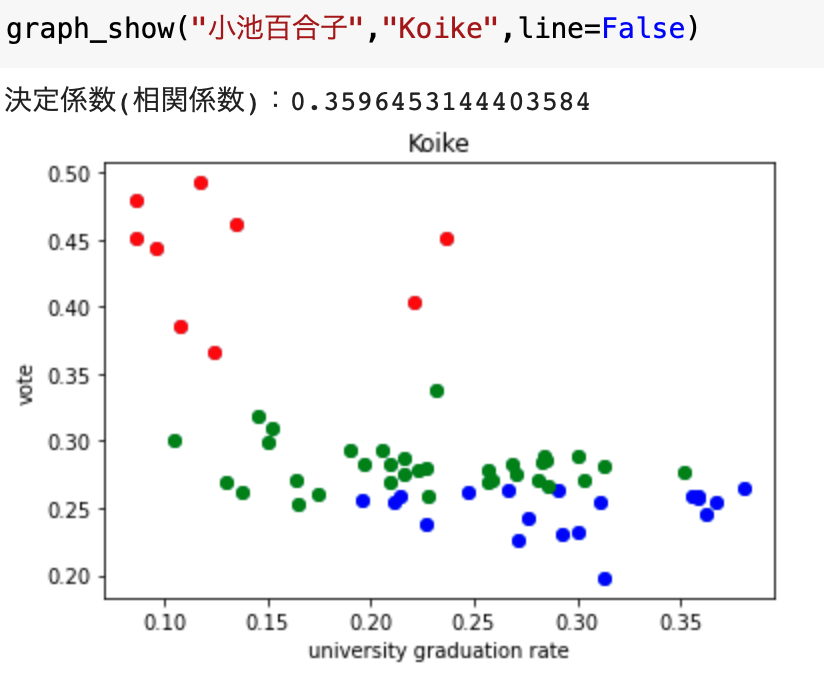決定係数は高くありませんが、クラスタリングは非常に上手くいっているのが分かります。
####宇都宮健児

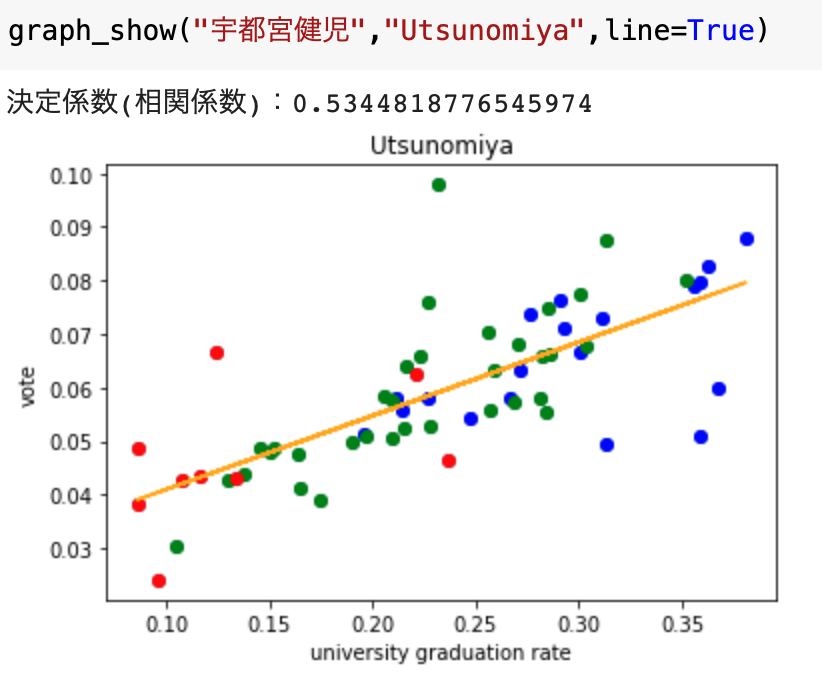そこそこの相関です。
####山本太郎

####小野泰輔

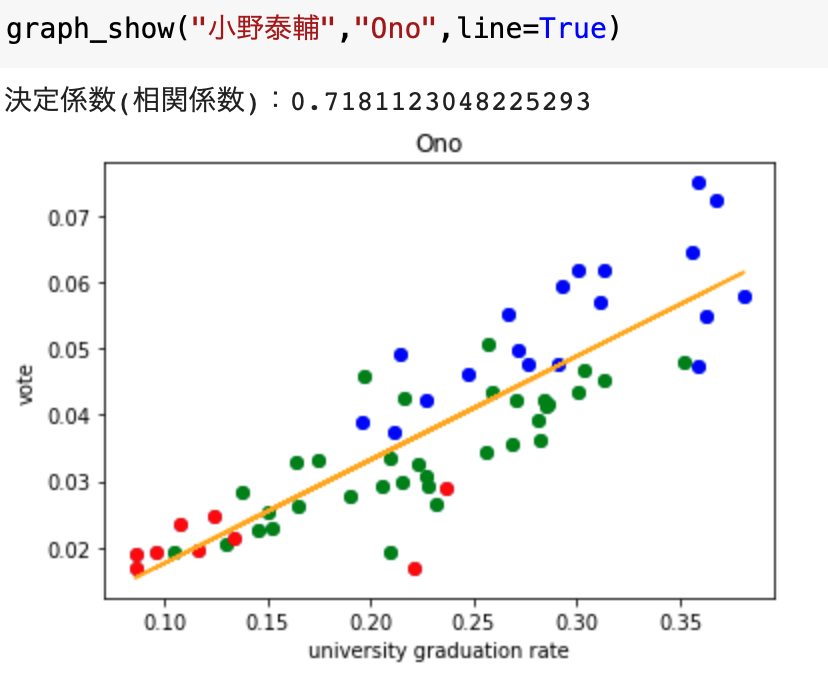これは正の相関があると言えそうです。。。
####桜井誠

##まとめ
「選挙結果は学歴と関係があるか？」というあけすけな問いから始まったデータ分析でしたが、一応最後に結論をまとめてみたいと思います。

その前に、今回のデータ分析における、不適切な（可能性のある）部分を確認しておきます。

• 票数のデータが自作（間違っているかもしれない）
• 学歴データが古い（2010年国勢調査）
• 学歴データと人口データ（2020）が同じ年のものでない
• 非有権者数を考慮していない
• 投票率を考慮していない

そういう訳で、初めにも書きましたが今回のデータ分析が有意なものかは全く保証できません。それを踏まえた上で、今回のデータ分析から少なくとも否定はされないであろう結論をまとめると、

• 選挙結果は地域の特性を反映している
• 候補者によっては票の入りかたに学歴（大学卒業者割合）と相関*がある

（*相関関係と因果関係は必ずしも一致するものではない）
といったところでしょうか。まあ想像に難くない結論だと個人的には思います。

個別の候補者についても色々分かることはありますが、ここでは割愛させていただきます。

---

以上、せっかくデータ分析を勉強しているのだからということで、フレッシュなデータを使って簡単なデータ分析をやってみましたが、今回使ったデータ以外にも色々なデータを組み合わせると他にも分かることがありそうですね。

個人的な感想としては、得票データの入力が面倒だったので、行政でなくてもいいから、少なくとも報道機関でまとめたデータをcsvとかで出してくれたらなあ・・・と思いました。（色々な制約があるのは分かりますが）