記事の目的
多次元ガウス分布の平均と分散共分散行列が未知のときの共役事前分布であるガウス-ウィシャート分布を使用し、Rを使ってベイズ推定します。
商品Aの購買個数と、商品Bの購買個数の平均と分散共分散行列を事後分布で推定します。
参考:ベイズ推論による機械学習入門
目次
0. モデルの説明
1. ライブラリ
2. 推定する分布
3. 事前分布
4. 事後分布
5. 予測分布
0. モデルの説明
1. ライブラリ
library(dplyr)
library(mvtnorm)
library(MCMCpack)
library(ellipse)
set.seed(100)
2. 推定する分布
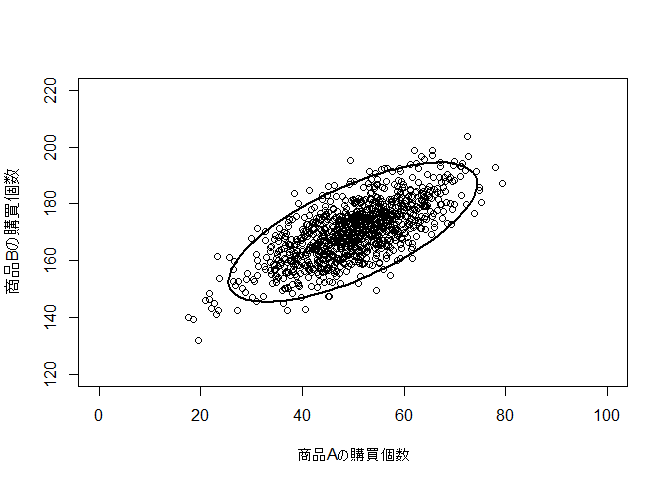
商品Aの購買個数と、商品Bの購買個数は、それぞれ平均が50, 170で、標準偏差が10, 相関係数が0.7の多次元ガウス分布に従います(適当)。
この真の分布の平均と共分散行列を事後分布で推定します。
# 真の共分散行列
sigma.true <- matrix(c(10^2, 0.7*10^2, 0.7*10^2, 10^2), ncol=2)
# 真の平均、共分散行列からサンプル
X.true <- rmvnorm(1000, mean = c(50, 170), sigma=sigma.true)
# 可視化
plot(X.true[,1],X.true[,2], xlim = c(0, 100), ylim = c(120, 220), xlab="商品Aの購買個数", ylab="商品Bの購買個数")
ell <- ellipse(sigma.true) + matrix(rep(c(50,170), each=100), nrow=100)
lines(ell, lw=2)
3. 事前分布
事前分布として、多次元ガウス分布の平均と分散共分散行列が未知のときの共役事前分布であるガウス-ウィシャート分布を指定します。
# ハイパーパラメータ
m0 <- c(0, 0)
beta0 <- 1/100^2
n0 <- 3
w.inv0 <- diag(2)*100
# パラメータ
lambda0 <- diag(2)
# 事前分布u
u.pre <- rmvnorm(1000, mean = m0, sigma=solve(lambda0*beta0))
par(mfrow=c(1,2))
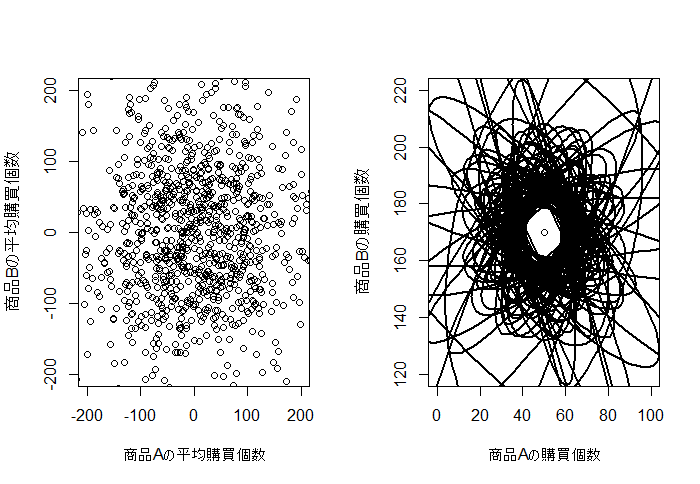
plot(u.pre[,1],u.pre[,2], xlim = c(-200, 200), ylim = c(-200, 200), xlab="商品Aの平均購買個数", ylab="商品Bの平均購買個数")
# 事前分布lambda
plot(50,170, xlim = c(0, 100), ylim = c(120, 220), xlab="商品Aの購買個数", ylab="商品Bの購買個数")
par(new=T)
for(i in 1:100){
w.pre <- riwish(n0, w.inv0)
ell <- ellipse(w.pre) + matrix(rep(c(50,170), each=100), nrow=100)
lines(ell, lw=2)
}
4. 事後分布
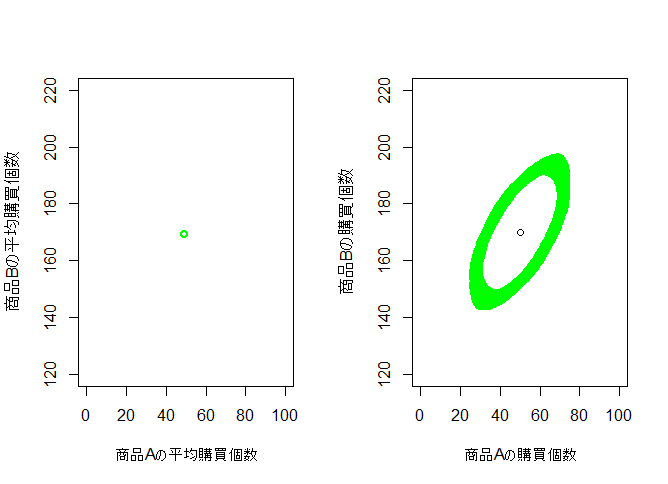
真の分布から100個サンプルを取って事後分布を推定します。
下図から、平均も分散共分散行列もうまく推定できていることが分かります。
X <- rmvnorm(100, mean = c(50, 170), sigma=sigma.true)
# 事後分布u
beta <- nrow(X)+beta0
m <- (apply(X, 2, sum)+(beta0*m0))/beta
X.sample <- rmvnorm(1000, mean = m, sigma=solve(beta*lambda0))
plot(X.sample[,1], X.sample[,2], xlim = c(0, 100), ylim = c(120, 220), col="green",
xlab="商品Aの平均購買個数", ylab="商品Bの平均購買個数")
# 事後分布lambda
n <- nrow(X)+n0
sum.tmp <- 0
for(i in 1:nrow(X)){
sum.tmp <- sum.tmp + (X[i,]) %*% t(X[i,])
}
w.inv <- sum.tmp + (beta0*m0%*%t(m0)) - (beta*m%*%t(m)) + w.inv0
plot(50,170, xlim = c(0, 100), ylim = c(120, 220),
xlab="商品Aの購買個数", ylab="商品Bの購買個数")
par(new=T)
for(i in 1:100){
w.post <- riwish(n, w.inv)
ell <- ellipse(w.post) + matrix(rep(c(50,170), each=100), nrow=100)
lines(ell, col="green", lw=2)
}
5. 予測分布
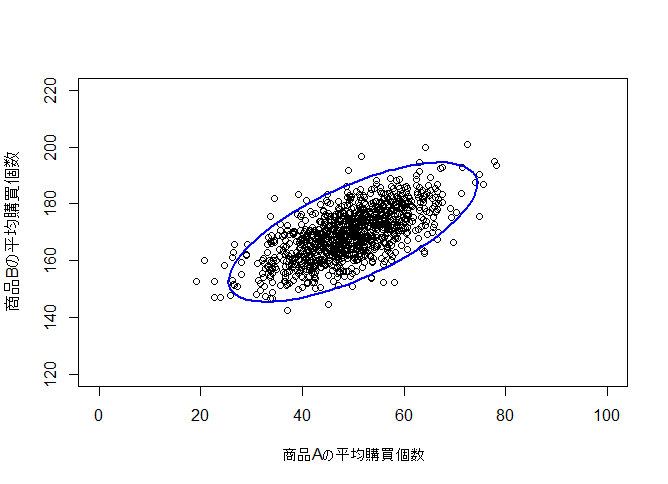
予測分布から1000個サンプルを取って可視化しました。
下図から、うまく推定できていることが分かります。
u.predict <- m
lambda.predict <- (1-2+n)*beta*solve(w.inv)/(1+beta)
n.predict <- 1-2+n
X.predict <- rmvt(1000, delta = u.predict, sigma = solve(lambda.predict), df = n.predict, type="shifted")
par(mfrow=c(1,1))
plot(X.predict[,1],X.predict[,2], xlim = c(0, 100), ylim = c(120, 220),
xlab="商品Aの平均購買個数", ylab="商品Bの平均購買個数")
ell <- ellipse(sigma.true) + matrix(rep(c(50,170), each=100), nrow=100)
lines(ell, col="blue", lw=2)