Rでベイズ線形回帰

記事の目的

線形回帰のパラメータをベイズ推定します。
参考：ベイズ推論による機械学習入門

目次

0. モデルの説明
1. ライブラリ
2. 推定する分布
3. 事前分布
4. 事後分布
5. 予測分布

0. モデルの説明

1. ライブラリ

library(dplyr)
library(mvtnorm)
library(scatterplot3d)
set.seed(100)

2. 推定する分布

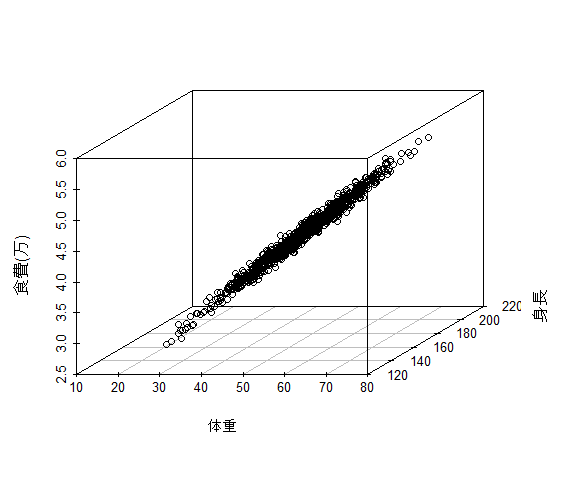
y=w1x1+w2x2を考えます。x1は体重、x2は身長、yは月の食費と仮定します。ｗ1,w2を500,100とし、これを推定するのが目的です。
ここで、体重は平均50で分散10, 身長は平均170で分散10の正規分布を仮定しています。
体重は因果関係が逆な気もしますが、気にしないでください。（笑）

w <- c(500, 100)
lambda <- 0.01
X.true <- rmvnorm(1000, c(50, 170), diag(2)*100)
y.true <- rnorm(1000, w[1]*X.true[,1] + w[2]*X.true[,2], 1/sqrt(lambda))
scatterplot3d(X.true[,1], X.true[, 2], y.true/10000,
              xlab="体重", ylab="身長", zlab="食費(万)",
              xlim=c(10,80), ylim=c(120, 210))

3. 事前分布

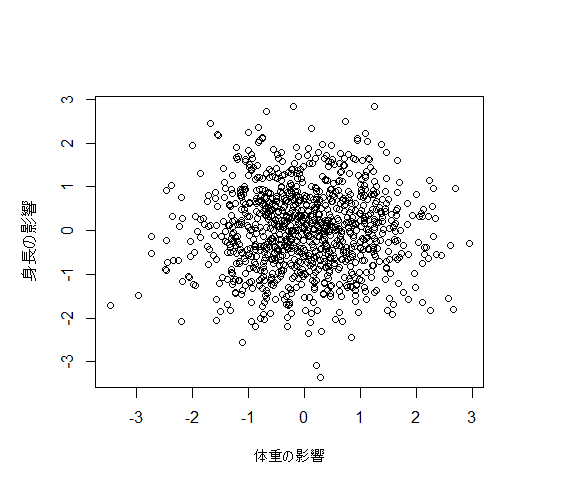
w1,w2の事前分布としてそれぞれ標準正規分布を仮定します。

m0 <- c(0, 0)
lambda0 <- diag(2)
w.pre <- rmvnorm(1000, m0, solve(lambda0))
plot(w.pre[,1], w.pre[,2],　xlab="体重の影響", ylab="身長の影響")

4. 事後分布

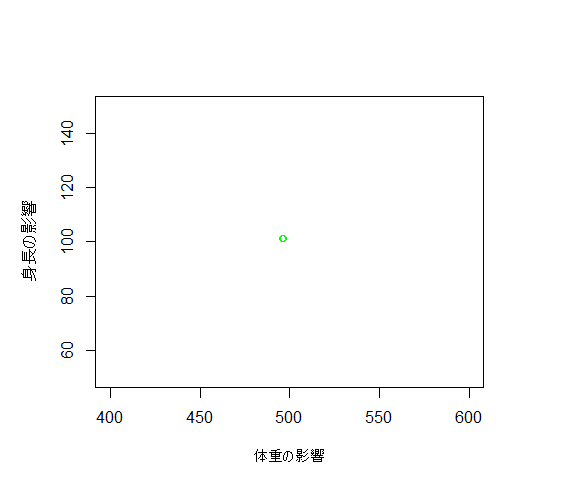
以下の図から、500, 100をうまく推定できていることが分かります。

X <- rmvnorm(100, c(50, 170), diag(2)*100)
y <- rnorm(100, w[1]*X[,1] + w[2]*X[,2], 1/sqrt(lambda))
sum.tmp <- 0
for(i in 1:nrow(X)){
  sum.tmp <- sum.tmp + X[i, ] %*% t(X[i, ])
}
lambda.post <- lambda*sum.tmp + solve(lambda0)
m.post <- solve(lambda.post) %*% (lambda*apply(y*X,2,sum) + lambda0%*%m0)
w.post <- rmvnorm(1000, m.post, solve(lambda.post))
plot(w.post[,1], w.post[,2],　xlab="体重の影響", ylab="身長の影響",
     xlim=c(400,600), ylim=c(50, 150), col="green")

5. 予測分布

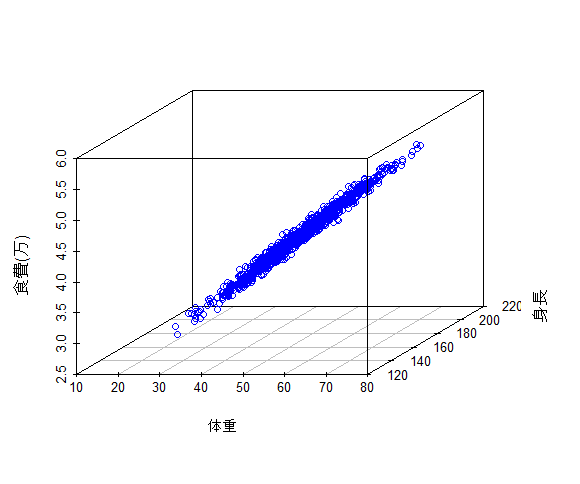
予測分布も、真の分布と似ていて、うまく推定できていることが分かります。

X.sample <- rmvnorm(1000, c(50, 170), diag(2)*100)
y.sample <- {}
for(i in 1:1000){
  u.post <- t(m.post) %*% X.sample[i, ]
  lambda.post.inv <- 1/lambda + t(X.sample[i, ]) %*% solve(lambda.post) %*% X.sample[i,]
  y.sample[i] <- rnorm(1, u.post, sqrt(lambda.post.inv))
}
scatterplot3d(X.sample[,1], X.sample[, 2], y.sample/10000,
              xlab="体重", ylab="身長", zlab="食費(万)",
              xlim=c(10,80), ylim=c(120, 210), color="blue")