記事の目的
カテゴリ分布と、その共役事前分布のディリクレ分布を使用し、Rを使ってベイズ推定を行います。
ある商品AのサイズS, サイズM, サイズLが選ばれる確率を推定します。
参考:ベイズ推論による機械学習入門
目次
0. モデルの説明
1. ライブラリ
2. 推定する分布
3. 事前分布
4. 事後分布
5. 予測分布
0. モデルの説明
1. ライブラリ
library(dplyr)
library(MCMCpack)
library(ggplot2)
library(gganimate)
set.seed(100)
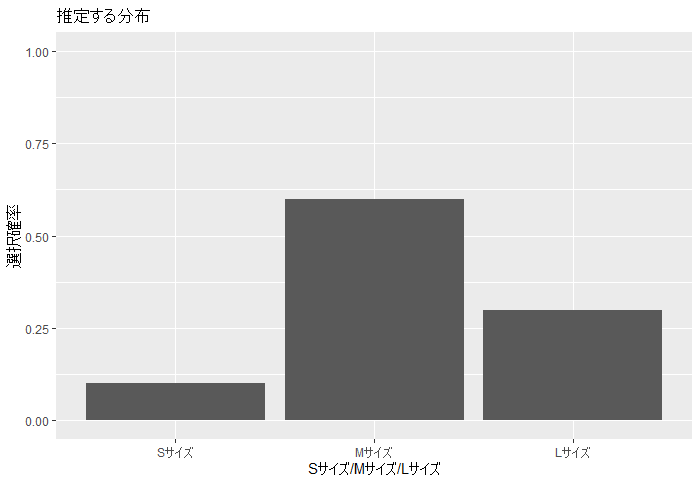
2. 推定する分布
商品AのサイズSが選ばれる確率は0.1, サイズMが選ばれる確率は0.6, サイズLが選ばれる確率は0.3ですが、僕たちはそれを知りません。
この、真の確率0.1, 0.6, 0.3を事後分布で推定します。
pi.true <- c(0.1, 0.6, 0.3)
NULL %>% ggplot(aes(x = c("Sサイズ", "Mサイズ", "Lサイズ"), y = pi.true)) +
geom_bar(stat = "identity") + ylim(0,1) +
labs(x="Sサイズ/Mサイズ/Lサイズ", y="選択確率", title="推定する分布") +
scale_x_discrete(limits=c("Sサイズ", "Mサイズ", "Lサイズ"))
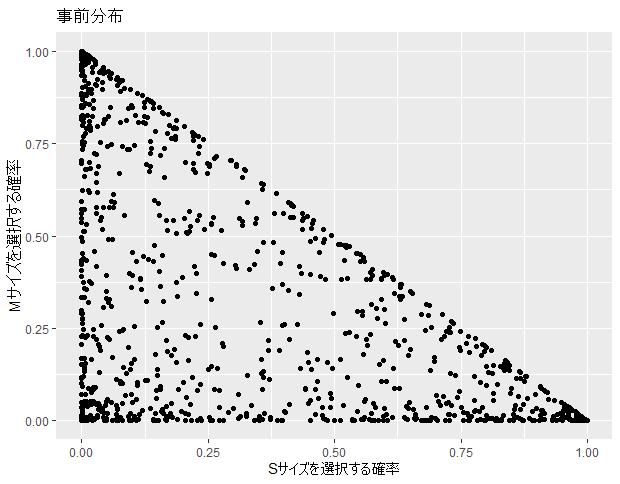
3. 事前分布
事前分布として、カテゴリカル分布の共役事前分布であるディリクレ分布を指定します。
この事前分布は、どの確率が出てもおかしくないような状態を表しています。
K <- 3
alpha0 <- rep(1/K, K)
X.pre <- rdirichlet(1000, alpha0)[,1:2]
NULL %>% ggplot(aes(x = X.pre[,1], y = X.pre[,2])) + geom_point() +
labs(x="Sサイズを選択する確率", y="Mサイズを選択する確率", title="事前分布")
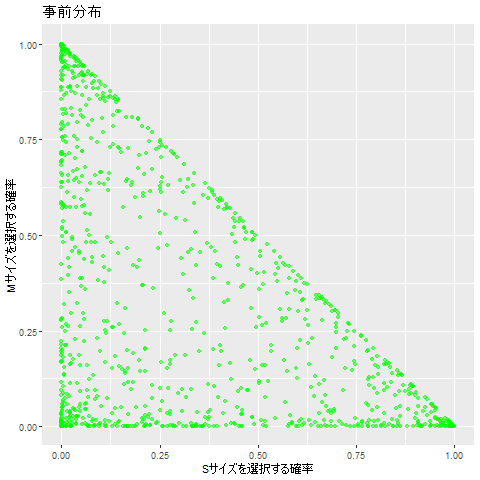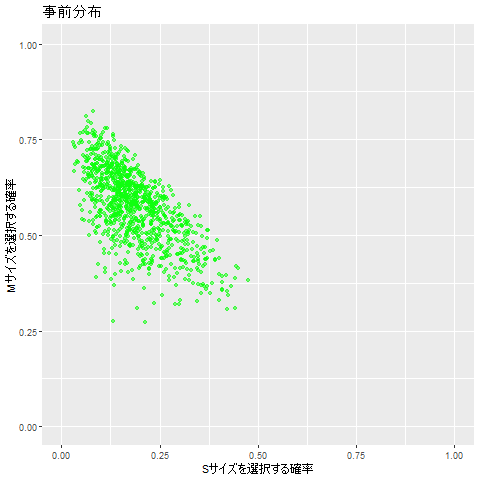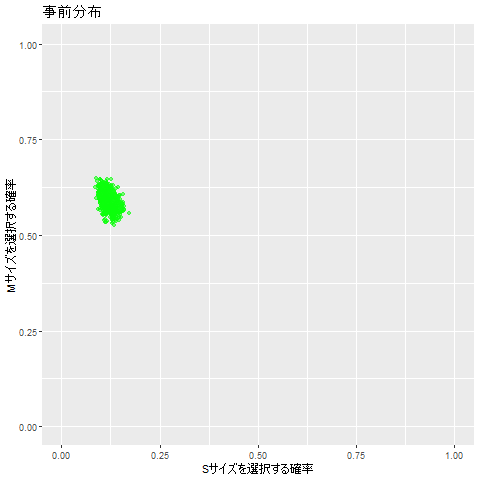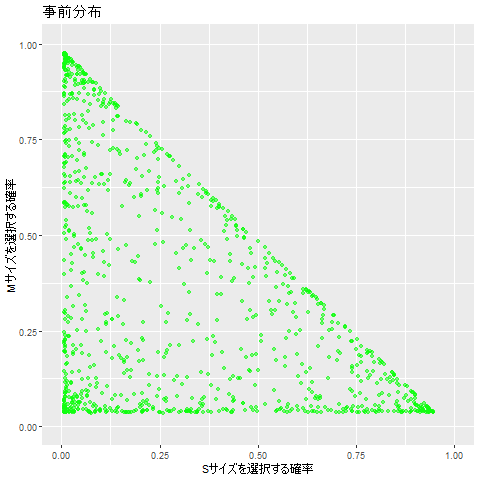
4. 事後分布
以下の図は、真の分布からのサンプルのデータを徐々に増やし、事後分布を推定する流れを表しています。
最終的には、サイズsが選ばれる確率が0.1, サイズMが選ばれる確率が0.6の付近に推定できています。
# ハイパーパラメータの初期値設定
alpha <- alpha0
# 可視化のためのデータ
Data <- rdirichlet(1000, alpha)[,1:2]
Data <- data.frame(Data, iter=rep(0,1000))
Data.pi <- data.frame(pi = alpha, iter=rep(0, 3))
# 事後分布
for(t in 1:3){
#データ発生
X <- rmultinom(10^t, 1, pi.true) %>% apply(2, which.max)
#パラメータ更新
n <- X %>% factor() %>% summary()
alpha <- n+alpha0
#可視化用データ取得
Data.tmp <- rdirichlet(1000, alpha)[,1:2]
Data.tmp <- data.frame(Data.tmp, iter=rep(t,1000))
Data <- rbind(Data, Data.tmp)
Data.pi.tmp <- data.frame(pi = alpha/sum(alpha), iter=rep(t,3))
Data.pi <- rbind(Data.pi, Data.pi.tmp)
}
# 事後分布可視化
Data %>% ggplot(aes(x=X1, y=X2)) +
geom_point(alpha=0.5, col="green") +
labs(x="Sサイズを選択する確率", y="Mサイズを選択する確率", title="事前分布") +
transition_states(iter, transition_length = 2, state_length = 1)
5. 予測分布
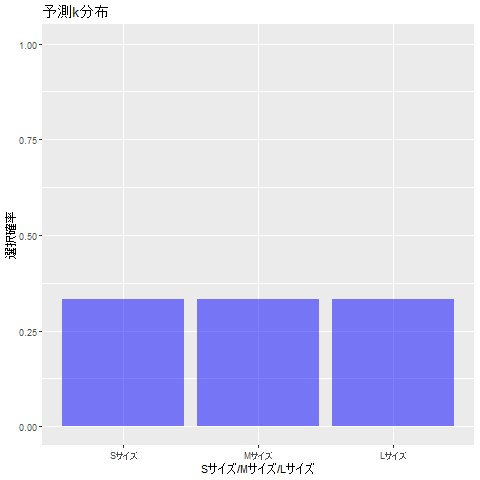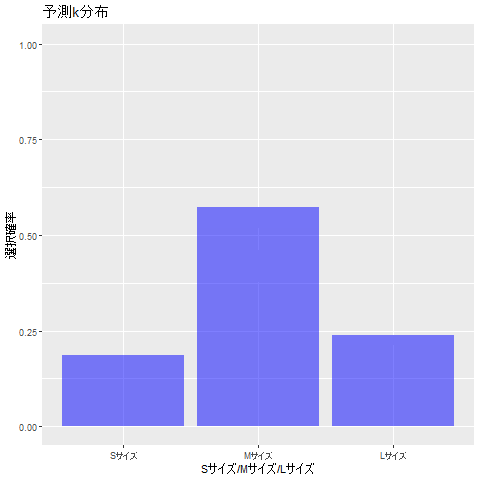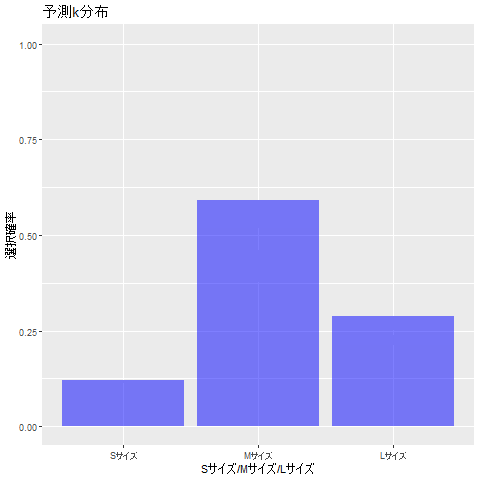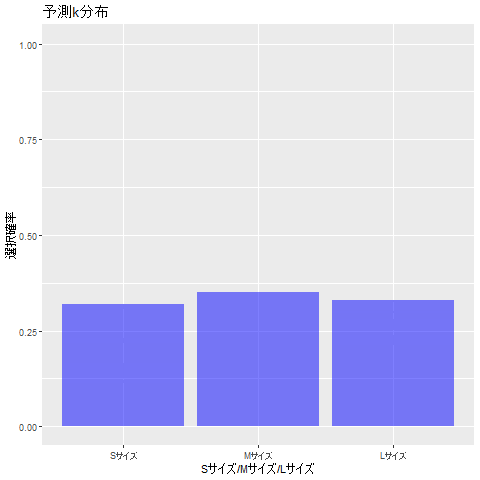
以下の図も、事後分布と同様に推定の流れを表しています。
最終的には、うまく確率の値を推定できています。
Data.pi$label <- rep(c("Sサイズ", "Mサイズ", "Lサイズ"), 4)
Data.pi %>% ggplot(aes(x=label, y=pi)) +
geom_bar(stat = "identity", alpha=0.5, fill="blue") +
ylim(0,1)+
labs(x="Sサイズ/Mサイズ/Lサイズ", y="選択確率", title="予測k分布") +
scale_x_discrete(limits=c("Sサイズ", "Mサイズ", "Lサイズ")) +
transition_states(iter, transition_length = 2, state_length = 1)