記事の目的
この記事の目的は、Rで無限混合ガウスモデルを実装することです。
参考: ノンパラメトリックベイズ 点過程と統計的機械学習の数理
目次
| No. | 目次
| 1 |
モデルの説明
|
2 |
データとライブラリ
|
3 |
実装
|
4 |
確認
|
|
1. モデルの説明
2. データとライブラリ
irisのデータセットを使用します。
X <- iris[,1:4]
D <- ncol(X)
N <- nrow(X)
library(mvtnorm)
library(MCMCpack)
library(cluster)
3. 実装
# (1)Kを求める
K <- 1
# (2)muを乱数で初期化
set.seed(100)
mu <- matrix(rep(apply(X,2,mean),each=K)+rnorm(K*D,0,2), nrow=K)
# (3)パラメータ初期値
a0 <- 1
b0 <- 1
alpha0 <- 10
t <- 1
# (4)(ⅰ)-(ⅳ)を繰り返す
max.iter <- 10
a <- a0 + N*D/2
n <- N
mu0 <- as.vector(rmvnorm(1, apply(X,2,mean), diag(D)))
for(s in 1:max.iter){
#(ⅰ)zのサンプリング
tmp <- t(apply(mu, 1, function(x) dmvnorm(X, x, diag(D)/t)))*
as.vector(n/(N-1+alpha0))
tmp2 <- dmvnorm(X, rmvnorm(1,mu0,diag(D)/t), diag(D)/t)*
as.vector(alpha0/(N-1+alpha0))
z <- apply(rbind(tmp,tmp2), 2, function(x) which.max(rmultinom(1,5,x)))
#k,nの更新
K <- z %>% unique() %>% length()
n <- tapply(z, z, length)
#(ⅱ)mu(µ)のサンプリング
x.k <- apply(X, 2, function(x) tapply(x, z, mean))
mu <- t(apply(cbind(x.k, n), 1,
function(x) rmvnorm(1, x[D+1]*x[1:(D)]/(x[D+1]+1)+1/(x[D+1]+1)*mu0,
diag(D)/(t*(x[D+1]+1)))))
#(ⅲ)t(τ)のサンプリング
b <- b0 + sum(unlist(apply(X, 2, function(x) tapply(x, z, function(x) (x-mean(x))^2))))/2 +
sum(as.vector(n/(2*(1+n)))*((t(t(x.k)-mu0)%*%(t(x.k)-mu0))*diag(K)))
t <- rgamma(1, a, b)
}
4. 確認
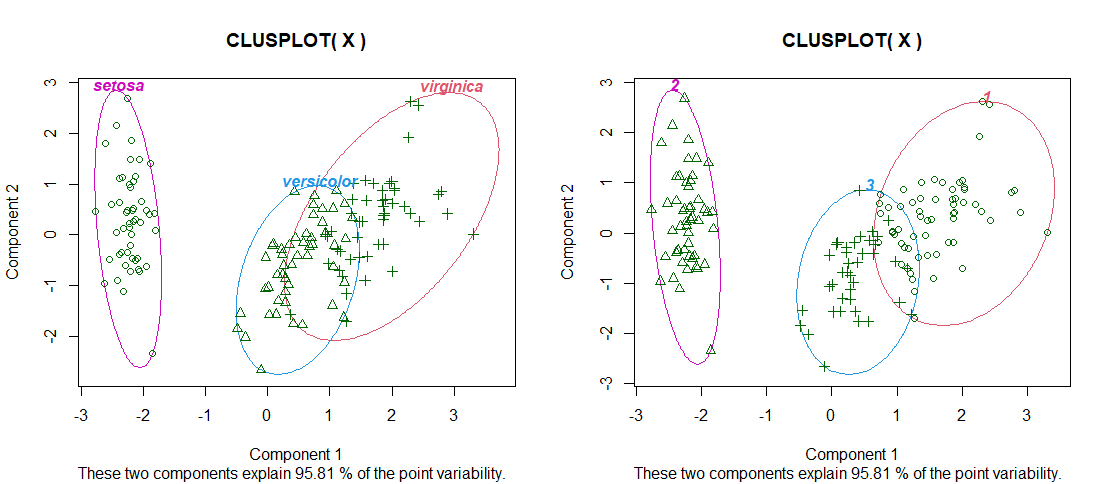
左が正解で、右が実装の結果です。
par(mfrow=c(1,2))
clusplot(X, iris[,5], color=TRUE, shade=FALSE, labels=4, lines=0)
clusplot(X, z, color=TRUE, shade=FALSE, labels=4, lines=0)