ベイズ推定での注意.1

記事の目的

この記事では、ベイズ推定での事前分布の設定で注意するべきポイントについてまとめました。
ベルヌーイ分布と共役事前分布のベータ分布を使用します。
ベルヌーイ分布のパラメータ(ベータ分布の値)をコインの表がでる確率だと考えて話を進めます。

目次

1. 事前分布の設定
2. データの生成
3. 事後分布の評価
4. データ量が多い場合

#1. 事前分布の設定
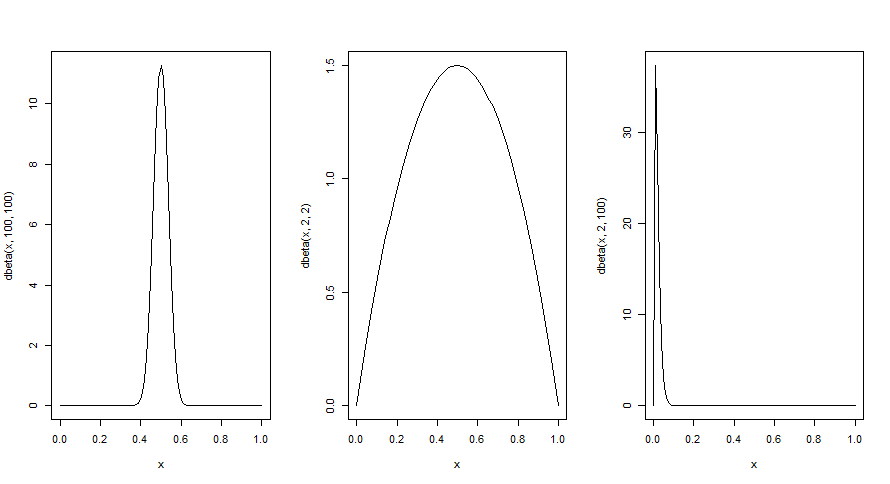
(1)コインの出る確率はほぼ間違いなく0.5だろう(確信が強い)と仮定している事前分布
(2)コインの出る確率は0.5かな(確信が弱い)と仮定している事前分布
(3)コインの出る確率はほぼ間違いなく0.2だろう(偏見が強い)と仮定している事前分布

par(mfrow=c(1,3))
curve(dbeta(x, 100, 100), 0,1) #(1)確信が強い
curve(dbeta(x, 2, 2), 0,1) #(2)確信が弱い
curve(dbeta(x, 2, 100), 0,1) #(3)偏見強い

#2. データの生成
コインの表が出る確率0.8の分布から、10個データを生成します。
このデータをもとに事前分布を更新して得られた事後分布で、0.8になる確率が高くなっていたら成功です。

N <- 10
set.seed(100)
X <- rbinom(N, 1, 0.8)
X
# 結果
[1] 1 1 1 1 1 1 0 1 1 1

#3. 事後分布の評価
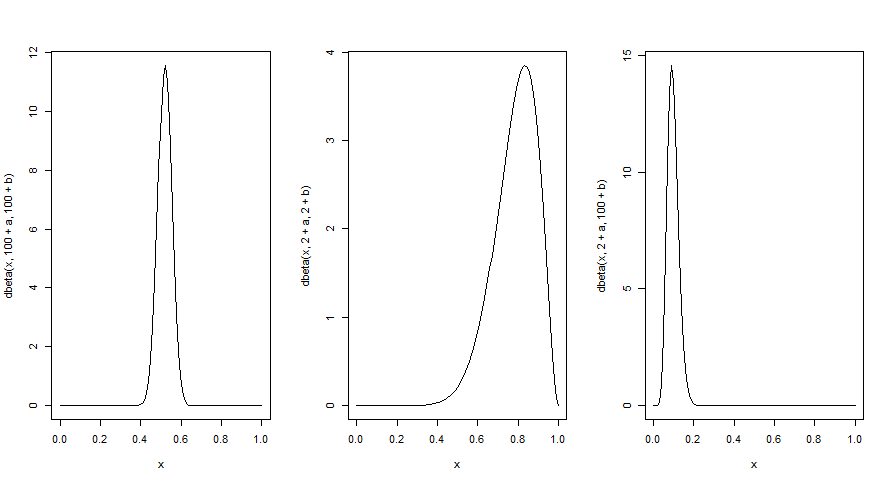
(1)確信が強い事前分布を仮定すると、データが少し得られても変わらない。
(2)確信が弱いため、少ないデータでも左右されやすく、うまく推定できている。
(3)確信が強い事前分布を仮定すると、データが少し得られても変わらない。
→適切な事前分布を仮定できれば、少ないデータ量でもうまく推定できる。
→誤って仮定すると、少ないデータ量だと間違った結果をまねく。

library(dplyr)
a <- X[X==1] %>% length()
b <- N-a
curve(dbeta(x, 100+a, 100+b), 0,1)
curve(dbeta(x, 2+a, 2+b), 0,1)
curve(dbeta(x, 2+a, 100+b), 0,1)

#4. データ量が多い場合
データ量を10から10000に変えて同様のことを行う。
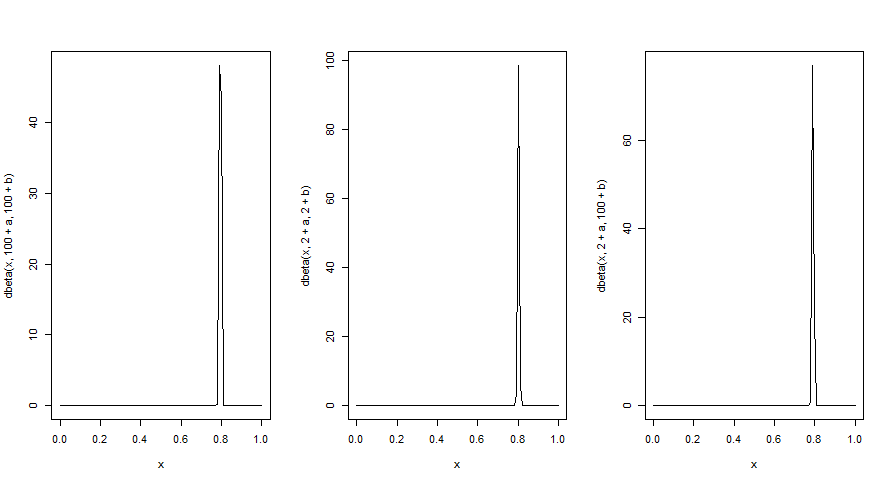
(1), (2), (3)全部うまく推定できている。
→データ量が多いと、事前分布に左右されずにうまく推定できる。

#データの生成
N <- 10000
set.seed(100)
X <- rbinom(N, 1, 0.8)
#ベイズ更新
a <- X[X==1] %>% length()
b <- N-a
curve(dbeta(x, 100+a, 100+b), 0,1)
curve(dbeta(x, 2+a, 2+b), 0,1)
curve(dbeta(x, 2+a, 100+b), 0,1)