記事の目的
混合ガウスモデルの周辺化ギブスサンプリングをRで実装します。
参考: ノンパラメトリックベイズ 点過程と統計的機械学習の数理
目次
| No. | 目次
| 1 |
モデルの説明
|
2 |
データとライブラリ
|
3 |
実装
|
4 |
確認
|
|
1. モデルの説明
2. データとライブラリ
データはirisのデータセットを使用します。
X <- iris[,1:4]
D <- ncol(X)
N <- nrow(X)
library(mvtnorm)
library(MCMCpack)
library(cluster)
3. 実装
# (1)Kを求める
K <- 3
# (2)muを乱数で初期化
set.seed(100)
z <- apply(rmultinom(N, 1, rep(1/K, K)), 2, which.max)
# (3)
a0 <- 1
b0 <- 1
alpha0 <- 1
# (4)(ⅰ)を繰り返す
max.iter <- 2
a <- 2*a0 + (N-1)*D
for(s in 1:max.iter){
#(ⅰ)zのサンプリング
for(i in 1:N){
#bの計算
b <- 2*b0 + sum(apply(X[-i,], 2, function(x) (x-mean(x))^2)) +
(N-1)/N*sum(apply(X[-i,], 2, mean)^2)
#mの計算
n <- tapply(z[-i], z[-i], length)
x.k <- apply(X[-i,], 2, function(x) tapply(x, z[-i], mean))
m <- as.vector(n/(n+1))*x.k
#zのサンプリング
tmp <- apply(m, 1, function(x) dmvt(X[i,], delta=x, df=a, sigma=solve(diag(D)*b/(1+1/N)), type="shifted", log=FALSE))*
(n+alpha0)/(sum(n)+alpha0)
z[i] <- which.max(rmultinom(1, 3, tmp))
}
}
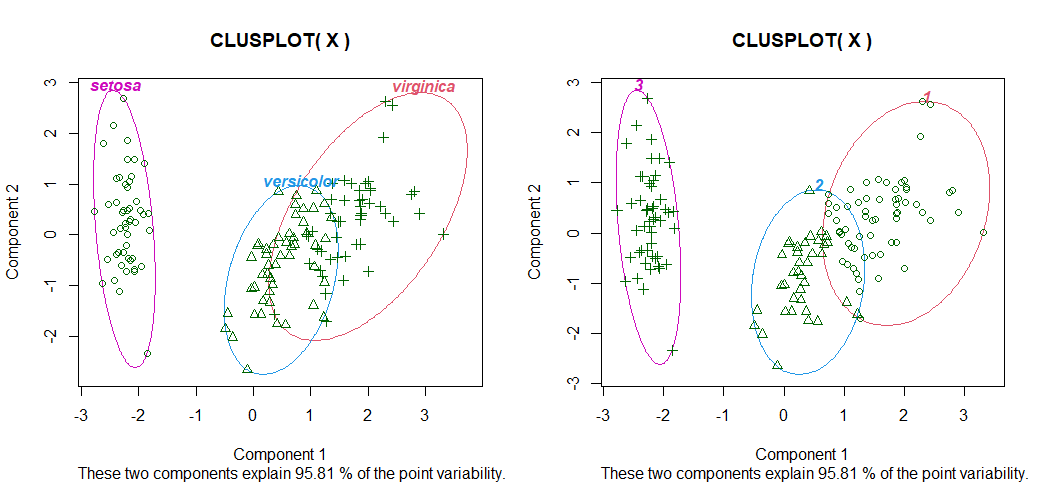
4. 確認
左が正解で、右が実装の結果です。
par(mfrow=c(1,2))
clusplot(X, iris[,5], color=TRUE, shade=FALSE, labels=4, lines=0)
clusplot(X, z, color=TRUE, shade=FALSE, labels=4, lines=0)