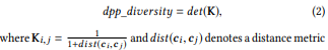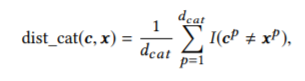反実仮想サンプル生成：「DiCE」 #Python

はじめに

ML (Machine Learning:機械学習)モデルの解釈は，ビジネスの現場における重要課題です．
推定精度の高いMLモデルを開発し，「出力と特徴量の対応関係」を評価することで，
ビジネス効果のある施策を打ち出すことが可能になります．
ex ：　「成功確率」（出力）が高くなる，「プロジェクトリーダーの条件」（特徴量）

近年，MLモデル解釈の方法として，「ELI5」「LIME」「SHAP」などの様々なアルゴリズムが開発されています．
これらアルゴリズムの内容は，「出力に対する特徴量の寄与度の計算」というもので，このような「寄与度の評価」では，モデルの解釈が「出力と特徴量の関係性の記述」に留まるため，出力最適化のためのサンプル特徴量の生成が難しい点があります．

Microsoft Researchが開発した「DiCE」は，反実仮想を考慮したモデル解釈アルゴリズムであり，目的とする出力を得るための特徴量サンプリングを可能にするアルゴリズムです．「サンプル生成による直接的な材料提供」という点において，他のアルゴリズムとは差別化されています．

本ブログでは，反実仮想を考慮したモデル解釈アルゴリズムである「DiCE」を取り上げ，原著論文の購読によるアルゴリズム理解と，実装による動作確認の概要をまとめます．

出典：

はじめに
MLモデルの解釈とは？
DiCEの概要
- DiCEとは？
- DiCEのコンセプト：「反実仮想サンプル生成」による「MLモデルの解釈」
DiCEのアルゴリズム説明と実装
- 使用データ
- サンプリングまでのフロー
- アルゴリズムのコンセプト
- 最適化関数の定義
- DiCEを使ってみる
まとめ
参考文献

MLモデルの解釈とは？

教師あり学習では与えられたデータに対して学習モデルが予測したラベルを返します．
このとき、MLでは以下の点が不透明です．

・学習モデルを作り、そこから得られた予測結果は正しいか？
・現象の因果関係を正しく学習できているか？

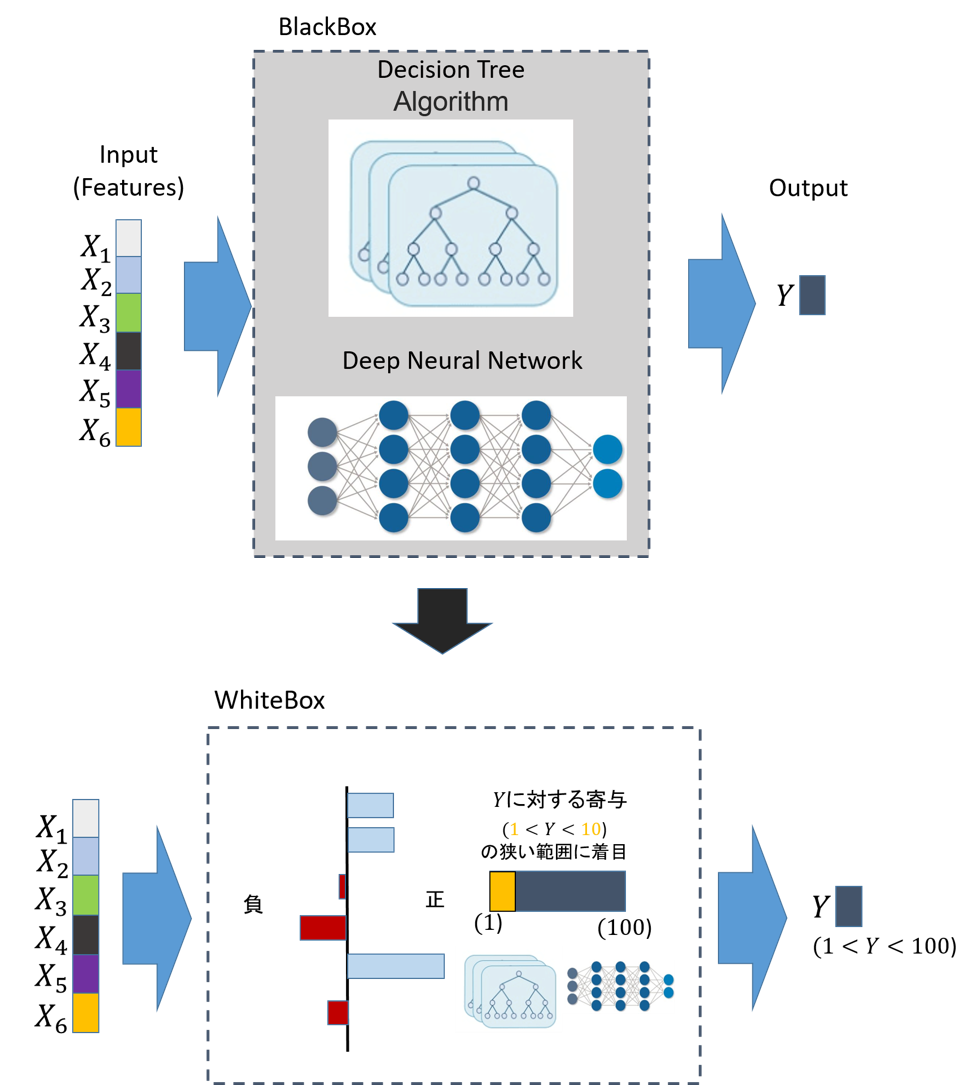
「MLの信頼性獲得」および「安全な実用」のためにも，上記疑問を解消するための，特徴量と出力（目的変数）の対応関係の評価が必要となります．本ブログでは，この対応関係の評価を「MLモデルの解釈」と表現します．

図：MLモデルの解釈とは？

余談ですが，「”MLの解釈性”というトピックを持つ論文数」は，過去20年において約４倍程度に増加しています．MLモデル理論の発展の実用化に伴い，ML人口が単純に増加したことも要因として考えられますが，一定数の興味を獲得するトピックであることは間違いなさそうです．
出典：https://beenkim.github.io/papers/BeenK_FinaleDV_ICML2017_tutorial.pdf

「DiCE」の概要

・DiCEとは？

Microsoft Researchの提供する，反実仮想サンプルを列挙するフレームワーク：Python ライブラリー

pip install dice_ml

出典：https://www.microsoft.com/en-us/research/project/dice/

・DiCEのコンセプト：「反実仮想サンプル生成」による「MLモデルの解釈」

反実仮想：事実と反対のことを想定すること．「もし～だったら…だろうに」のような言い方

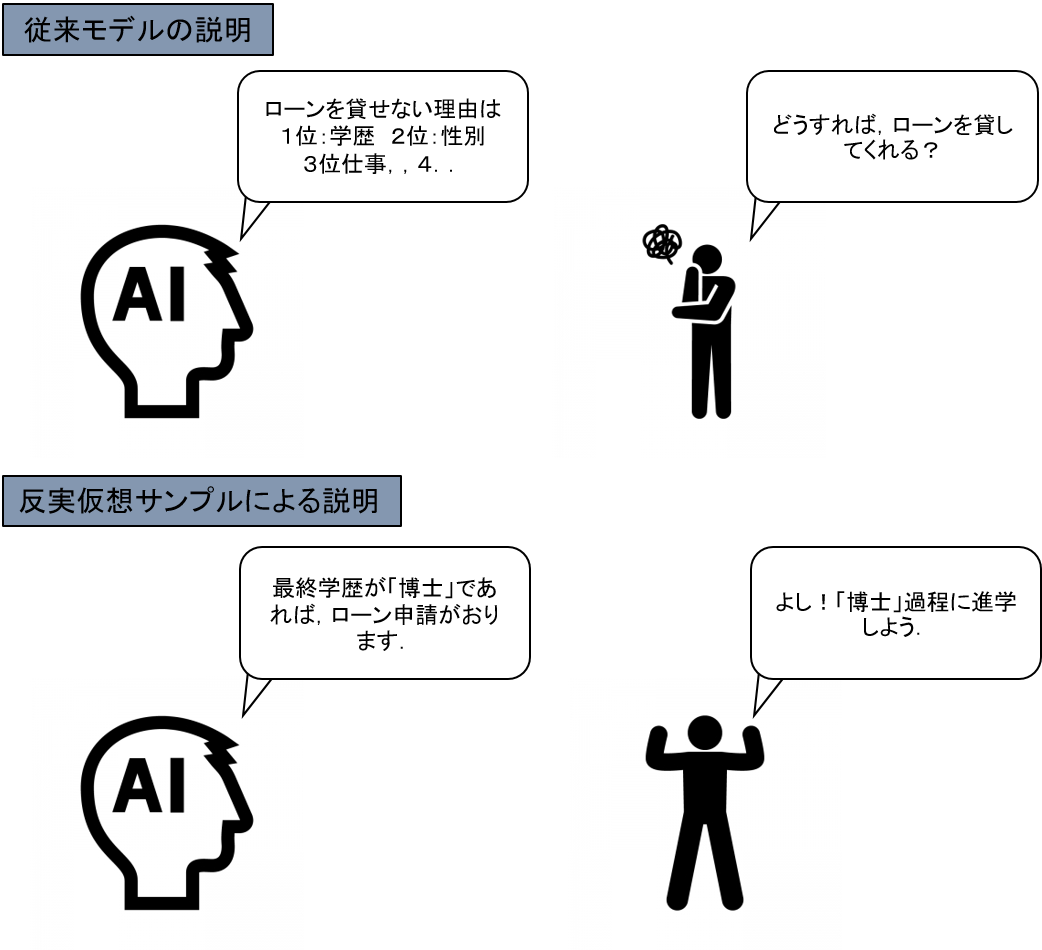
図：反実仮想モデルによるMLモデルの解釈

現在，「ELI5」「LIME」「SHAP」など，「出力と特徴量の関係性」を記述するためのアルゴリズムが開発されています．各アルゴリズムの基本コンセプトは「出力に対する特徴量の寄与度の算出」であり，寄与度の「正負」「大小」から出力との関係性を解釈できます．

しかし，一方で「寄与度」のみが算出される「出力と特徴量の関係性の記述」だけでは，出力最適化のための「最適特徴量」を算出することができません．

例えば，図のような「ローン貸出審査」を行う機械学習モデルが，任意の候補者の貸出判定を実施する場合を考えます．任意の候補者の特性は，「年齢」「学歴」「過去の借入履歴」などの変数で特徴づけられ，機械学習モデルは，事前に学習したパターンにより，その候補者の貸出の判定をします．

そして，仮に，モデルが候補者の貸出を「拒否」と判定したとします．

この場合，従来の解釈アルゴリズムでは，「なぜ候補者が拒否されたか」を説明することができますが，「では，この候補者はどうすれば借入できるか」の具体提案を出すことはできません．

この問題を解決したのが，DiCEの基本コンセプト：「反実仮想サンプル生成」になります．

DiCEでは，既存のMLモデルからは反実仮想に当たるサンプルを生成し，直接的な改善案を提示することができます．
出典：https://qiita.com/OpenJNY/items/ef885c357b4e0a1551c0

DiCEのアルゴリズム説明と実装

・使用データ

本ブログでは，DiCEアルゴリズムの説明のため，「Bank Marketing Data Set from UCI Machine Learning Repository」データを使います．

本データは，複数の社会人に関する特徴量とloan貸出判定が記載されているデータで，目的変数 y を loan={0:No, 1:Yes}と設定します．

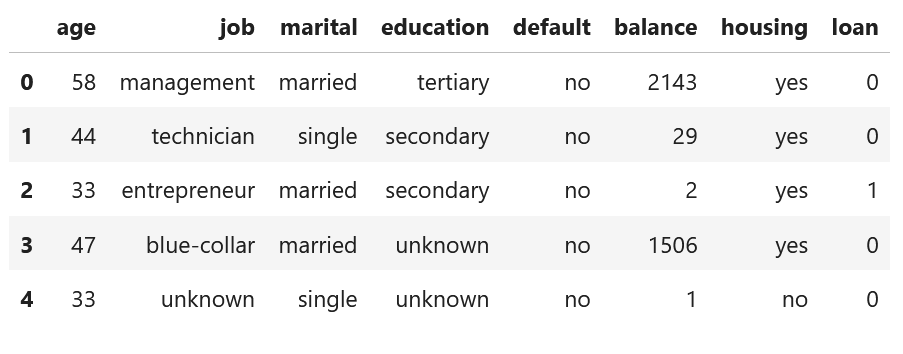
表：Bank Marketing Data Set:データセット内の一部のカラムのみ表示

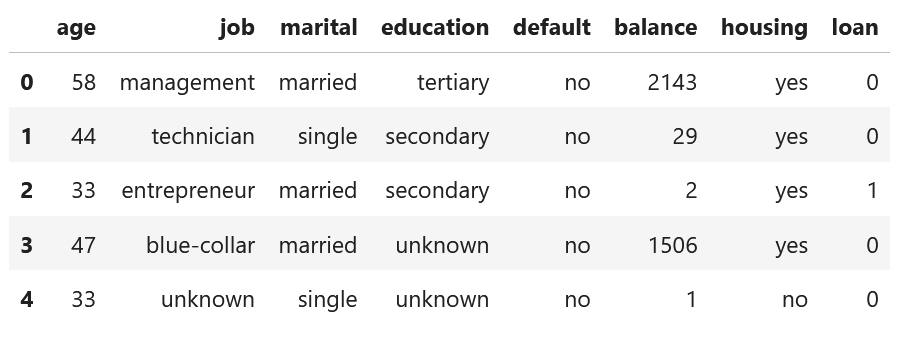
出典：http://archive.ics.uci.edu/ml/datasets/Bank+Marketing#

・サンプリングまでのフロー

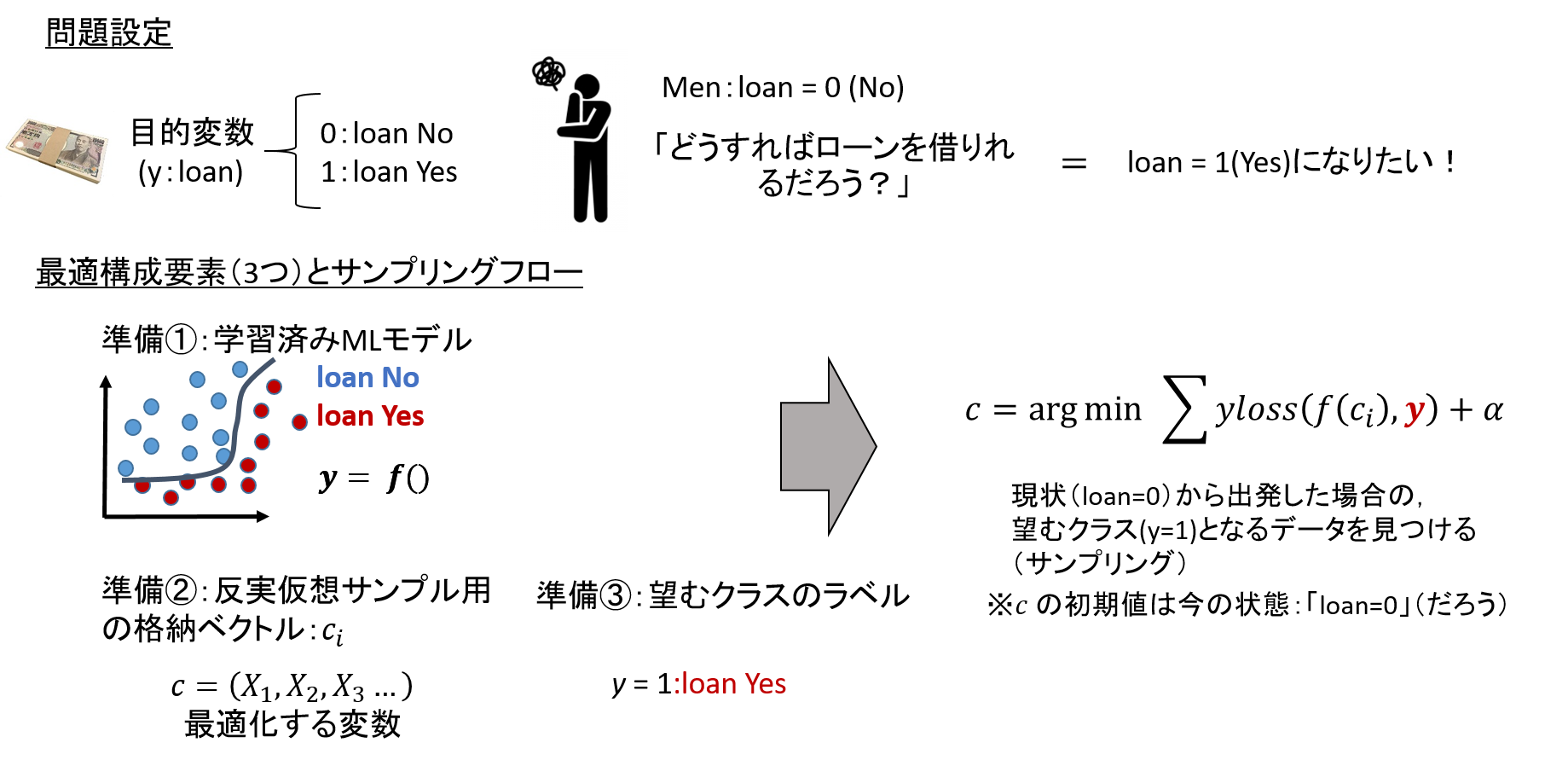
本解説における問題設定とサンプリングの方針を下記に示します．

（問題設定）
１．ローンを借りれない候補者がいる（loan=0:No）
２．loanと特徴量を学習したMLモデルが開発されている．
３．候補者は，に，loan=1:Yes（反実仮想）になるための条件を，モデルよりサンプリングする．

（サンプリング方針）
反実仮想サンプル用の格納ベクトルcを用意し，MLモデルより出力f(c)を算出
→そのラベルが望むクラス（loan=1）になった場合に小さくなる損失関数を定義
→極値を取るときのサンプルcを抽出する．　＝　反実仮想サンプル

図：問題設定とサンプリングフロー

・アルゴリズムのコンセプト

DiCEには，上記最適化関数の最小化において，実装されているいくつかの工夫があります．それら７つのコンセプトをここでご説明します．
また，以下に出てくる式は原著論文から引用しております．
出典：https://www.microsoft.com/en-us/research/publication/explaining-machine-learning-classifiers-through-diverse-counterfactual-examples/

１．「実現可能性」
事実ベクトル（loan =0：No）に対して離れすぎたものを反実仮想ベクトル（c）としてサンプリングしても，現実味がなく，実現することができません．

そのため，DiCEでは，評価関数に，ベクトル（loan =0：No）と反実仮想ベクトル（c）の距離を追加し，距離が遠くなりすぎないような最適化をかけています．

２．「ダイバーシティ」
複数の反実仮想ベクトル（c）をサンプリングする場合，多種な選択パターンがあったほうが嬉しく，類似したベクトルが含まれていて欲しくありません．

そのため，複数の反実仮想ベクトル（c_i）間の距離を定義し，その値ができるだけ遠くなるように最適化をかけます．

３．「損失関数にhinge lossを採用」
SVMなどに使用されることのあるhinge関数がlossとして活用されています．

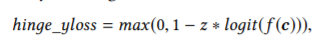
４．「連続変数とカテゴリー変数の区別」
DiCEでは，多次元データ間の距離を算出し，「実現可能性」と「ダイバーシティ」を定義しています（１．２．）．
その際，連続的な分布をとる連続変数と，ダミー変数化したカテゴリー変数は，分布の仕方の違いにより，区別して距離を計算しています（おそらくです．．．間違えているかも）

５．「分散を考慮した距離の算出による特徴量の重み調整（連続変数）」
多次元のベクトルの距離を考える場合，平均値（または中央値）だけでは，データ群同士の適切な距離を測ることができません．なぜならば，次元の変数ごとに分散が異なる場合，データの広がりによりデータ群の距離が変化するからです．こういった場合には，マハラビス距離のような分散を考慮した距離を考慮する必要があります．DiCEでは，平均値よりもロバストな「中央値によるばらつき：MAD」を用いて，連続変数に関する距離を分散考慮型へと変換しています．

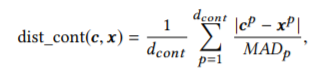
MAD：median absolute deviation

MADが大きい変数に関して，重み付けを行わない場合には，「より広い範囲での値変動」が起きるため，実現不可能な非現実的な特徴量がサンプリングされることになります．

６．「変化させる特徴量の選択」
反実仮想サンプリングの実問題として，変更できない特徴量が存在します．
※性別や若返りなど
そのため，DiCEでは，変更する特徴量を選択できるようになっています（最適化の際に，可変に設定しなければ良いだけです）

７．「実現可能性とダイバーシティのトレードオフ」

DiCEの定義する最適化関数には，「実現可能性」と「ダイバーシティ」の重みを設定するハイパーパラメータが存在します．本値を調整することにより，それぞれの比率を変化させられます．
（また，本レポートでは記述がないが，有益なサンプリングかどうかの評価指標が存在しているらしいため，その指標の活用よりパラメタチューニングができるのだと思っています）

・最適化関数の定義

上記コンセプトを考慮したうえで，最適化する関数を定義します．

反実仮想ベクトル（c_i）のサンプリングロジックと，各コンセプトを考慮したうえで，最適化関数は以下のように記述できます．

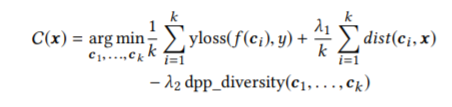
λ1とλ2はハイパーパラメータ

・DiCEを使ってみる

それでは，DiCEを使って，実際に反実仮想サンプルを生成してみます．

なお，本実装はMicrosoft社ドキュメント(GitHub)を参照しています．
出典：https://www.microsoft.com/en-us/research/project/dice/

#Library import
import pandas as pd
import numpy as np
import dice_ml
import tensorflow as tf
from tensorflow import keras
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)

#データの読み込み＆目的変数のダミー変数化
data = pd.read_csv('bank-full.csv'
                   ,sep=';'
                   ,usecols=['age', 'job', 'marital', 'education', 'default', 'balance', 'housing','loan'])
data['loan'] = pd.get_dummies(data.loan,drop_first=True)
data.head()

#DiCE用にデータ構造を定義
d = dice_ml.Data(dataframe=data, continuous_features=['age', 'balance'], outcome_name='loan')

#MLモデルの学習
train, _ = d.split_data(d.normalize_data(d.one_hot_encoded_data))
X_train = train.loc[:, train.columns != 'loan']
y_train = train.loc[:, train.columns == 'loan']

model = keras.Sequential()
model.add(keras.layers.Dense(20, input_shape=(X_train.shape[1],), kernel_regularizer=keras.regularizers.l1(0.001), activation=tf.nn.relu))
model.add(keras.layers.Dense(1, activation=tf.nn.sigmoid))
model.compile(loss='binary_crossentropy', optimizer=tf.keras.optimizers.Adam(0.01), metrics=['accuracy'])
model.fit(X_train, y_train, validation_split=0.20, epochs=100, verbose=0, class_weight={0:1,1:2})

#DiCEオブジェクトにMLモデルをprovide
backend = 'TF'+tf.__version__[0] # TF1
m = dice_ml.Model(model=model, backend=backend)

#反実仮想サンプリングモデル
exp = dice_ml.Dice(d, m)
#query instanceの設定：反実仮想を求める基準値の設定（であると理解してます）
query_instance = {'age':20,
                  'job':'blue-collar',
                  'marital':'single',
                  'education':'secondary',
                  'default':'no',
                  'balance': 129,
                  'housing':'yes'}
#反実仮想サンプリングの生成
dice_exp = exp.generate_counterfactuals(query_instance
                                        ,total_CFs=4
                                        ,desired_class="opposite")
#total_CFs：生成するベクトルの数
#desired_class：生成したいサンプルのクラス：反実仮想の場合にはopposite

#サンプル結果の可視化
dice_exp.visualize_as_dataframe()

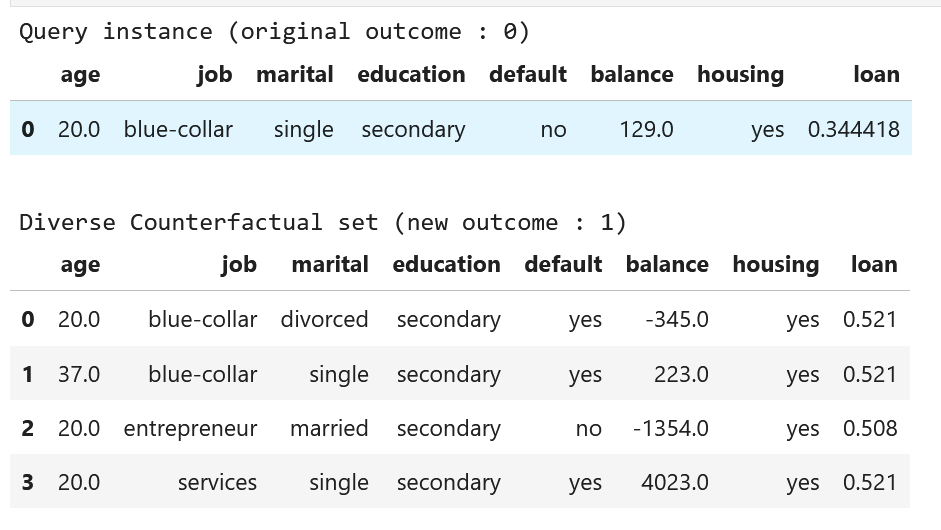
サンプル結果を見ると，outcome=0に対し，outcome=1のサンプルが4つ生成されていることが分かります．
loanのカラムは，sigmoid関数に対する入力値であり，outcome=0が約0.3に対し，outcome=1が0.5以上になっていることが分かります．
※MLモデルを上手く作れなかったので微妙な結果になりました．．．

特徴量を見ると, age, job, maritalなどが変化していることが分かります．
確かに，設定したquery_instanceとは異なる特徴量が生成されていることが分かります．

また，「特徴量に対する重みの変更」や「変化させる特徴量の指定」を行う場合には以下のように設定します．

feature_weights = {'age': 1}#ageの重み→1
features_to_vary = ['age','job']#ageとjobだけ変化させる
dice_exp = exp.generate_counterfactuals(query_instance
                                        ,total_CFs=4
                                        ,desired_class="opposite"
                                        ,feature_weights=feature_weights
                                        ,features_to_vary=features_to_vary)

まとめ

本ブログでは，反実仮想を考慮したモデル解釈アルゴリズムである「DiCE」を取り上げ，原著論文の購読によるアルゴリズム理解と，実装による動作確認の概要をまとめてみました．DiCEは「サンプル生成による直接的な材料提供」という点において，他のアルゴリズムとは差別化されたものであり，多角的なモデルの解釈に貢献してくれるものかと思います．
原著論文の内容は記載内容だけでなく，まだフォローしていない点がありますし，間違い等あるかと思います．
ご指摘いただけると幸いです．

以上です．

参考文献

・Welcome to ELI5’s documentation!（ELI5）
https://eli5.readthedocs.io/en/latest/
・"Why Should I Trust You?": Explaining the Predictions of Any Classifier（LIME）
https://arxiv.org/abs/1602.04938#:~:text=version%2C%20v3)%5D-,%22Why%20Should%20I%20Trust%20You%3F%22%3A%20Explaining,the%20Predictions%20of%20Any%20Classifier&text=In%20this%20work%2C%20we%20propose,model%20locally%20around%20the%20prediction.

・LIMEで機械学習の予測結果を解釈してみる
https://qiita.com/fufufukakaka/items/d0081cd38251d22ffebf
・Explainable AI: ELI5,LIME and SHAP（kaggle kernel）
https://www.kaggle.com/kritidoneria/explainable-ai-eli5-lime-and-shap
・DiCE: Diverse Counterfactual Explanations for Machine Learning Classifiers（DiCE）
https://www.microsoft.com/en-us/research/project/dice/
https://arxiv.org/pdf/1905.07697.pdf（転記してある数式はすべてここから）
・DiCE: 反実仮想サンプルによる機械学習モデルの解釈/説明手法
https://qiita.com/OpenJNY/items/ef885c357b4e0a1551c0
・入門統計的因果推論：Judea Pearl (著), Madelyn Glymour (著), Nicholas P. Jewell (著), 落海浩 (翻訳)
https://www.amazon.co.jp/%E5%85%A5%E9%96%80-%E7%B5%B1%E8%A8%88%E7%9A%84%E5%9B%A0%E6%9E%9C%E6%8E%A8%E8%AB%96-Judea-Pearl/dp/4254122411
・CounterFactual Machine Learningの概要 (反実仮想機械学習)
https://usaito.github.io/files/190729_sonyRD.pdf
・Interpretable Machine Learning: The fuss, the concrete and the questions
https://beenkim.github.io/papers/BeenK_FinaleDV_ICML2017_tutorial.pdf

反実仮想サンプル生成：「DiCE」