はじめに
「Advent Calendarの記事内容がまとまってない...」
3日前の著者のセリフです.
はい.こんにちわ.BrainPadの@Tano9876です.
皆さんは,「やろうと思ってたけどついつい先延ばしにしてしまった..」みたいな経験ありますか?
著者は今回やってしまいましたよ.
advent calendarで記事出すと決めたあの日は凄いやる気だったのに,気が付けばあれよあれよと時が過ぎ,金曜日仕事が終わって土日を満喫し情熱大陸で月曜への活力を蓄えていたその時,Qiita運営から届いていた1通の通知
「え..あと3日..」
情熱大陸見てる暇ありませんでした.
(カニ職人の特集でしたね.おいしそうでしたね)
ということで!今回は,先延ばしにした自分を正すため,
遅延割引効果とその数理モデルを勉強し,言語化および図示化をすることとで頭と体に先延ばしの原理を叩き込みます.
また,遅延割引効果の機械学習との関係や心理学的な実験的研究による知見の紹介も行います.
目次
- はじめに
- 遅延価値割引とは
- 数理モデルでの表現
- 問題設定
- 遅延価値割引率の説明
- 遅延価値割引のモデル
- 準双曲型割引モデルの利点
- 遅延価値割引を抑えるには
- モデルからの学び
- 実験的研究からの知見
- 機械学習との関係
- まとめ
- 参考文献
遅延価値割引とは
遅延価値割引とは,
“遅延価値割引(delay discounting またはtemporal discounting )とは報酬が得られるまでの
遅延によって、報酬の価値が低下することである。一般的に、すぐに獲得できる報酬のほうが遅延報酬よりも好まれる。“
3: https://waseda.repo.nii.ac.jp/index.php?action=repository_action_common_download&item_id=2024&item_no=1&attribute_id=162&file_no=1&page_id=13&block_id=21#:~:text=遅延価値割引(delay discounting,報酬よりも好まれる。
(出典より引用)
つまり,「未来の報酬や負担を少なく見積もる」現象のことを指します.

数理モデルでの表現
問題設定
-
題材:社会人
締め切りまでに「何かしらの課題」を提出しなければならない. -
前提
・この人は,「課題は初日に終わらせます!」という優等生ではない
・1日の作業時間には限度がある(1日1時間とか) -
変数
x1:1日の作業可能時間(hour)
N:締め切り日程(4月N日)
n:作業開始した時点からの残り日数(day)
T:課題の完了にかかる客観的時間(hour) -
行動
課題が完了するために必要な時間を主観的に見積もり,締め切り日に提出できるよう「課題着手日」を決める.

遅延価値割引率の説明
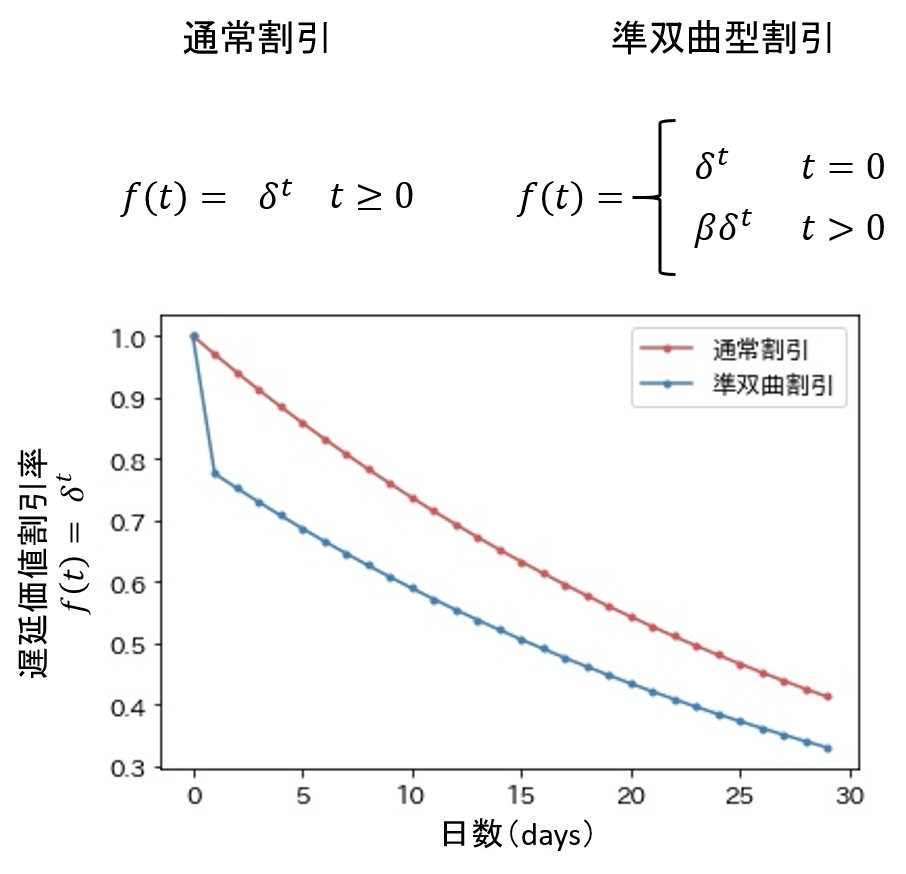
遅延価値割引効果における主役の変数は,「時刻tでの遅延価値割引率:$\delta^t$」です.
これは,0-1の値である割引率$\delta$の時刻ごとの累積値であり,未来になるほど価値が大きく割り引かれる様子をモデル化できます.たとえば,今すぐ($t=0$)に貰える「1万円」の主観的価値は,明日($t=1$)になると$「1万円×\delta^1$」になり,明後日($t=2$)には$「1万円×\delta^2$」になります.
著者が学んだ文献では,この遅延割引として「準双曲型割引」を採用していました.
これは,$t=1$以降の割引率に0-1の値である$\beta$を掛け合わせたモデルで,通常割引に比べて$t=0$から$t=1$にかけての割引率の減少が急激なのが特徴です.
遅延価値割引のモデル
今回モデル化するのは,「いつから課題を始めようか」と考える社会人の心理です.
検討初日を4月1日とし,
N=30日:4月30日を課題の締め切りとします.
また,課題の完了には客観的にT=20(hour)かかるとし,
1日の作業可能時間を1(hour/day) とします.
また,価値割引率$\delta = 0.97$,$\beta=0.8$とします.
この場合,作業日数N=30日に対し作業可能時間を1(hour/day)かつ課題の完了時間T=20(hour)であるため,
4月30日 - 20日 = 4月10日から課題に着手すれば最終日には提出できると客観的に見積もれます.
しかし,冒頭の内容通り,人間の主観には「遅延価値割引」が発生します.
これから社会人の主観的な見積もりをモデル化します.

- 4月1日($t=0$)
4月1日の段階で,初日から課題着手しようか迷う心理を考えます.
$t=0$では,締め切りまでの日数はn=30日であり,1日当たりの主観的必要時間(hour/day)は以下のように見積もられます.
\frac{20}{30-0}×\delta^0=\frac{20}{30-0}×1=0.666..
この見積もりは1日の作業可能時間:1(hour/day)より少ないため,「今日からはじめなくてもきっと終わるだろう」と考え,明日以降に課題着手をずらします.
※$t=0$では,価値割引率が$\delta^0=1$であるため,遅延価値割引は発生せず,客観的な見積もりと同値になります.
- 4月2日($t=1$)
次に,4月1日の段階で4月2日から課題着手しようか迷う心理を考えます.
$t=1$では,締め切りまでの日数はn=29日であり,1日当たりの主観的必要時間(hour/day)は以下のように見積もられます.
\frac{20}{30-1}×\beta×\delta^1=\frac{20}{30-1}×0.8×0.97=0.535..
この見積もりは,$t=0$と同様,1日の作業可能時間:1(hour/day)より少ないため,「明日からはじめなくてもきっと終わるだろう」と,またもや明後日以降に課題着手をずらします.
※$t=1$では.遅延価値割引が発生し,客観的なものに比べ楽観的な見積もりを行います.
- 4月$x$日($t=(x-1)$)
最後にこれらを一般化して,4月1日の段階で4月$x$日から課題着手しようか迷う心理を考えます.
$t=(x-1)$では,締め切りまでn=30-$x$日残っており,1日当たりの主観的必要時間(hour/day)は以下のように見積もられます.
\frac{20}{30-(x-1)}×\beta×\delta^{(x-1)}
# 問題設定
N = 30
sub_hour_per_day = 1
T = 20
days = np.arange(0,N)
remaining_days = N - days
delta = 0.97
beta = 0.8
# 主観的必要時間の計算
df_estimates = pd.DataFrame()
df_estimates['t'] = days
df_estimates['n'] = N - days
Discounting = df_estimates['n'].apply(lambda n : beta*(delta**(N-n)) if n!=N else 1)
T_init = [T for i in range(days.shape[0])]
df_estimates['T'] = (Discounting * T_init)
df_estimates['obj_hour_per_day (hour/day)'] = df_estimates['T'] / df_estimates['n']
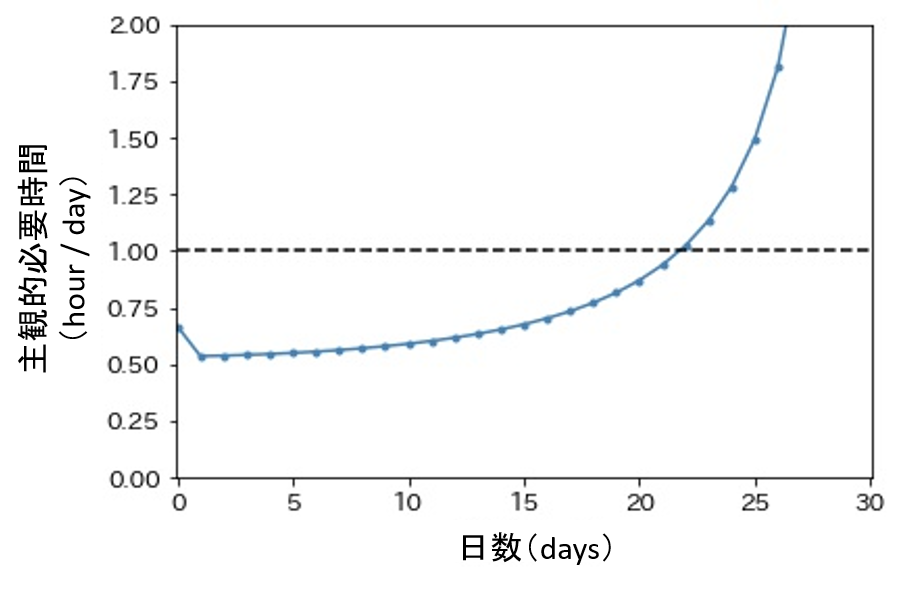
これら結果を見ると,1日当たりの主観的必要時間が1日の作業可能時間:1(hour/day)を超えるのが,4月22日($t=21$)であり,この時点にてはじめて「22日から始めたら間に合わないので,21日から始めよう!」と課題着手を計画します.
しかし,$t=20$の場合の1日当たりの客観的必要時間(hour/day)は,
\frac{20}{30-20}=2.0
と,1日の作業可能時間:1(hour/day)より多いため,実際に作業を開始すると,「ヤバイ.終わらない.早く始めればよかった..」と絶望することになります.
これが,遅延価値現象 $\fallingdotseq$ サボり現象のモデル化です.
準双曲型割引モデルの利点
準双曲型割引を使う利点は,課題着手当日(4月21日)になったときの心変わりを表現できるところにあります.
前章にて社会人は,4月21日に課題を着手することを4月1日の段階で計画しました.
では今度は,4月21日当日になった場合の心理を考えます.
- 4月21日($t=0$)
$t=0$では,締め切りまでの日数はn=10日であり,1日当たりの主観的必要時間(hour/day)は以下のように見積もられます.
\frac{20}{30-20}×\delta^0=\frac{20}{30-20}×1=2.0
ここで,社会人が「本当に今日から始める必要があるかな?」と計画延長を再検討している状況を考えます.

- 4月22日($t=1$)
次に,4月21日の段階で4月22日から課題着手しようか迷う心理を考えます.
$t=1$の場合では,締め切りまでの日数はn=9日であり,1日当たりの主観的必要時間(hour/day)は以下のように見積もられます.
\frac{20}{30-21}×\beta×\delta^1=\frac{20}{30-21}×0.8×0.97=1.724...
この見積もりは,$t=0$(4月21日)に比べ少ないため,「今日から始めなくても終わりそうだな」と考えてしまい,計画当日(4月21日)以降に課題着手をずらしてしまいます.
この心変わりの結果は,準双曲型割引モデルの「$t=0$から$t=1$にかけて割引率が急激に減少する」という特徴によるものであり,人間の怠惰な性格を表現したものと言えます.
遅延価値割引効果を抑えるには?
さて,これまで遅延価値割引現象のモデルをみてきました.
サボるという現象は,遅延価値割引による未来の負担の楽観的見積もりであることがわかりました.
では,どうすれば,この楽観的見積もりの癖を改善できるのでしょうか?
ここでは,前章のモデルに加え,心理学の実験的研究での知見も踏まえ,改善の方法を模索します.
モデルからの学び
遅延価値割引現象の自覚する(楽観的な計画見積もりと当日の心変わり)
自身の気持ちのなかで発生する現象を意識し,俯瞰的に自己を見つめることで,行動がコントロールできる.
実験研究からの学び
このような論文を発見しました.
「感謝をする」とサボらずにすむみたいです.
 ""The emotion gratitude reduces impatience even when…""
""「感謝をする」という気持ちは,遅延価値割引の程度を抑える ""
""The emotion gratitude reduces impatience even when…""
""「感謝をする」という気持ちは,遅延価値割引の程度を抑える ""
4: https://journals.sagepub.com/doi/pdf/10.1177/0956797614529979
5: https://sites.google.com/site/tabuchimegumi/research/2014nian-ji-du-lun-wen/%E3%80%8Cganxiewosuru%E3%80%8Dtoiuqichichihachiyansizhigeyinnochengduwoyieru%E3%80%82
(出典より引用)
機械学習との関係
さいごはざっくばらんに調べた論文を載せます.
- temporal discountingと強化学習を扱っている論文
6: https://www.frontiersin.org/articles/10.3389/fnbeh.2014.00076/full
7: https://www.sciencedirect.com/science/article/pii/S0004370215000557
8: sciencedirect.com/science/article/pii/S0893608012002146
- ランダムフォレストモデルの特徴量にdelay discountingを使った値を使用
アルコール依存症の治療に対するモチベーション分類
9: https://psyarxiv.com/ahwsg/
禁煙治療の分類
10: https://academic.oup.com/ntr/article-abstract/22/3/415/5228675
まとめ
-
サボるという現象は,遅延価値割引による未来の負担の楽観的見積もり
-
「感謝をする」とサボらずにすむ
「感謝かんしゃkansya......今週の輪講の準備はじめます」
以上です.
参考文献
1: https://www.amazon.co.jp/s?k=その問題+数理モデルが解決します&i=stripbooks&__mk_ja_JP=カタカナ&crid=MAO7W8LO0ARX&sprefix=その問題%2Cstripbooks%2C263&ref=nb_sb_ss_i_2_4
2: https://www.amazon.co.jp/社会科学のための-ベイズ統計モデリング-統計ライブラリー-浜田-宏/dp/4254128428/ref=asc_df_4254128428/?tag=jpgo-22&linkCode=df0&hvadid=342392667096&hvpos=&hvnetw=g&hvrand=4755202878119981087&hvpone=&hvptwo=&hvqmt=&hvdev=c&hvdvcmdl=&hvlocint=&hvlocphy=1009340&hvtargid=pla-848621526676&psc=1&th=1&psc=1
3: https://waseda.repo.nii.ac.jp/index.php?action=repository_action_common_download&item_id=2024&item_no=1&attribute_id=162&file_no=1&page_id=13&block_id=21#:~:text=遅延価値割引(delay discounting,報酬よりも好まれる。
4: https://journals.sagepub.com/doi/pdf/10.1177/0956797614529979
5: https://sites.google.com/site/tabuchimegumi/research/2014nian-ji-du-lun-wen/%E3%80%8Cganxiewosuru%E3%80%8Dtoiuqichichihachiyansizhigeyinnochengduwoyieru%E3%80%82
6: https://www.frontiersin.org/articles/10.3389/fnbeh.2014.00076/full
7: https://www.sciencedirect.com/science/article/pii/S0004370215000557
8: sciencedirect.com/science/article/pii/S0893608012002146
9: https://psyarxiv.com/ahwsg/
禁煙治療の分類
10: https://academic.oup.com/ntr/article-abstract/22/3/415/5228675