9軸センサで相補フィルタ使って姿勢推定

この記事は高知工科大 Advent Calendar 2018の12日目の記事です。

はじめに

9月末に行われた室内飛行ロボコン自動操縦部門に、回路・制御担当として参加してきました。
この記事ではそれに使った機体の姿勢推定について書きます。

概要

加速度3軸、ジャイロ3軸、地磁気3軸の9軸センサを使って姿勢推定をしました。
姿勢はクォータニオンとして保持します。

9軸相補フィルタできた
理論上はヨー軸の誤差も補正してくれるはず…(>_<) pic.twitter.com/q2rrQKkDB2

— Niwa🐔 (@Niwa_t0r1) 2018年6月23日

だいぶ前の動画ですがこんな感じになります。

クォータニオンについて

クォータニオンを使うと姿勢を1つのスカラーと3つのベクトルで表現することができます。

\boldsymbol{q}=q_0+q_1\boldsymbol{i}+q_2\boldsymbol{j}+q_3\boldsymbol{k}

クォータニオンは 回転軸の単位ベクトル$\boldsymbol{n}$ と、 回転角$\theta$ で表すことができ、
クォータニオン$\boldsymbol{q}$は以下の式(1)のようになります。

\boldsymbol{q}=\cos{\frac{\theta}{2}}+\boldsymbol{n}\sin{\frac{\theta}{2}}\tag{1}

つまり、$\boldsymbol{n}=[n_x,n_y,n_z]^{T}$だとすると

\begin{bmatrix}
q_0 \\
q_1 \\
q_2 \\
q_3
\end{bmatrix}
=
\begin{bmatrix}
\cos{\frac{\theta}{2}} \\
n_x\sin{\frac{\theta}{2}} \\
n_y\sin{\frac{\theta}{2}} \\
n_z\sin{\frac{\theta}{2}} 
\end{bmatrix}

となります。

クォータニオンを用いると、ベクトルや座標系の回転を三角関数を用いずに処理できます。
例えば、回転後のベクトルを$\boldsymbol{r^{'}}$、回転を表すクォータニオンを$\boldsymbol{q}$とすると以下の式(2)のようになります。

\boldsymbol{r^{'}}=\boldsymbol{q}\boldsymbol{r}\boldsymbol{q^{-1}}\tag{2}

なお、$\boldsymbol{q^{-1}}$は$\boldsymbol{q}$の逆クォータニオンで、$\boldsymbol{q}$の逆回転を表すクォータニオンになります。以下で求められます。

\boldsymbol{q^{-1}}=\cos{\frac{\theta}{2}}-\boldsymbol{n}\sin{\frac{\theta}{2}}

考えてみれば当然ですが、回転軸単位ベクトルの符号を反転させるとそのまま逆回転になります。

さて、式(2)の計算を進めていきます。

\boldsymbol{r^{'}}
=A\boldsymbol{r}

とおくと、行列$A$は以下の3x3行列で表せます。

A=
\begin{bmatrix}
q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3)        & 2(q_1q_3+q_0q_2) \\
2(q_1q_2+q_0q_3)        & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_2q_3-q_0q_1) \\
2(q_1q_3-q_0q_2)        & 2(q_2q_3+q_0q_1)        & q_0^2-q_1^2-q_2^2+q_3^2
\end{bmatrix}

この行列$A$を、回転行列または方向余弦行列 (DCM)といいます。

また、クォータニオン同士の積は行列で表すと以下のようになります。

qp=
\begin{bmatrix}
q_0 & -q_1 & -q_2 & -q_3 \\
q_1 & q_0  & -q_3 & q_2 \\
q_2 & q_3 & q_0 & -q_1 \\
q_3 & -q_2 & q_1 & q_0
\end{bmatrix}
\begin{bmatrix}
p_0 \\
p_1 \\
p_2 \\
p_3 
\end{bmatrix}\tag{3}

以上の基礎知識をもとに、姿勢推定を考えます。

参考：オイラー角への変換

Z-Y-X系オイラー角のベクトル回転行列$R$は以下のようになります。

R=
\begin{bmatrix}
\cos\theta \cos\psi & \sin\phi \sin\theta \cos\psi - \cos\phi \cos\psi & \cos\phi \sin\theta \cos\psi + \sin\phi \sin\psi \\
\cos\theta \sin\psi & \sin\phi \sin\theta \sin\psi + \cos\phi \cos\psi & \cos\phi \sin\theta \sin\psi + \sin\phi \cos\psi \\
-\sin\theta & \sin\phi \cos\theta & \cos\phi \cos\theta
\end{bmatrix}

つまりこの$R$が$A$と一致するので、各要素を比較することでクォータニオンをオイラー角に変換できます。

\begin{bmatrix}
\phi \\
\theta \\
\psi
\end{bmatrix}
=
\begin{bmatrix}
\arctan \frac{2(q_2q_3+q_0q_1)}{q_0^2-q_1^2-q_2^2+q_3^2} \\
\arcsin (-2(q_1q_3-q_0q_2)) \\
\arctan \frac{2(q_1q_2+q_0q_3)}{q_0^2+q_1^2-q_2^2-q_3^2}
\end{bmatrix}

ジャイロのみ姿勢推定

ジャイロセンサから取得できる角速度を$\boldsymbol\omega=[\omega_x,\omega_y,\omega_z]^{T}$とすると、クォータニオン$\boldsymbol{q}=[q_0,q_1,q_2,q_3]^{T}$は以下の微分方程式で表せます。

\frac{d}{dt}
\begin{bmatrix}
q_0 \\
q_1 \\
q_2 \\
q_3
\end{bmatrix}
=
\frac{1}{2}
\begin{bmatrix}
0        &-\omega_x &-\omega_y &-\omega_z \\
\omega_x & 0        & \omega_z &-\omega_y \\
\omega_y &-\omega_z & 0        & \omega_x \\
\omega_z & \omega_y &-\omega_x & 0
\end{bmatrix}
\begin{bmatrix}
q_0 \\
q_1 \\
q_2 \\
q_3
\end{bmatrix}\tag{4}

これを時間で積分してやると姿勢のクォータニオンが得られます。
しかしながら、ジャイロセンサのみだと、ジャイロセンサの誤差が積分で累積してしまい、ドリフトが発生してしまいます。

ジャイロ+加速度センサで姿勢推定

よって、ジャイロセンサの誤差を加速度センサで補正します。
方法としては、カルマンフィルタが有名ですね。今回は比較的直感的に理解しやすい方法を使った相補フィルタを用います。

考え方としては、もしジャイロセンサに誤差が存在しないと仮定すると、角速度のみで更新したクォータニオンで加速度ベクトルを回転させた場合、そのベクトルは重力加速度のベクトル$\boldsymbol{g}=[0,0,1]^{T}$に一致するはず。一致しなかった場合、そこから一致させるような回転のクォータニオンをつくり係数をかけ、角速度のみで更新したクォータニオンにかけることで補正するというものです。

文章だとわからないと思うので、ステップごとに図解してみます。

1.ジャイロセンサのみで姿勢推定

まず、ジャイロセンサのみでクォータニオンを更新します。このクォータニオンを$\boldsymbol{q_{\omega}}$とすると、式(4)と同様にクォータニオンを更新できます。

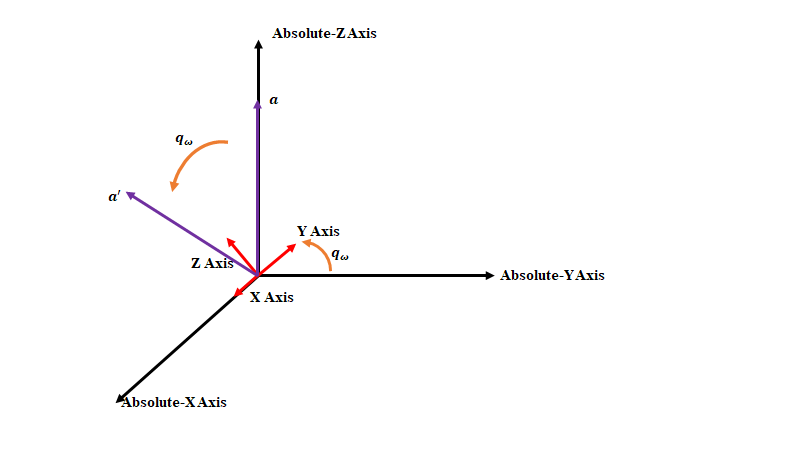
$\boldsymbol{q_{\omega}}$で表される回転は、以下の図のようになります。黒矢印が絶対軸、赤矢印がセンサ軸を表します。

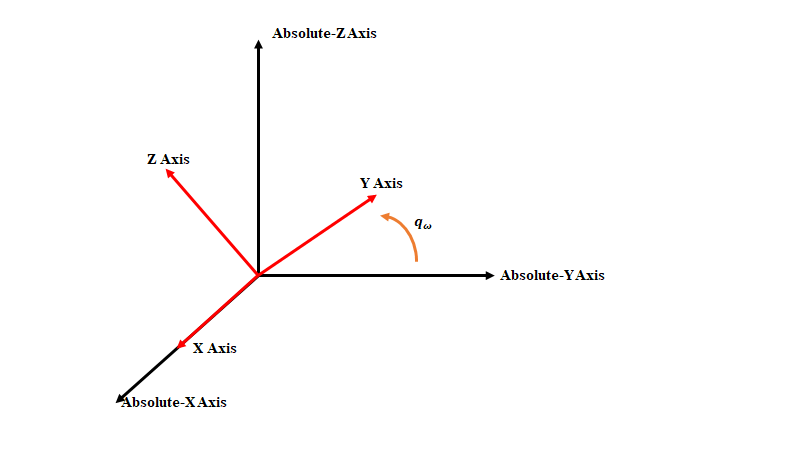
2.加速度ベクトルを更新したクォータニオンで回転

加速度センサより取得した加速度ベクトル$\boldsymbol{a}=[a_x,a_y,a_z]^T$を$\boldsymbol{q_{\omega}}$で回転させます。回転後の加速度ベクトルを$\boldsymbol{a^{'}}$とすると、式(2)より以下のようになります。

\boldsymbol{a^{'}}=\boldsymbol{q_{\omega}}\boldsymbol{a}\boldsymbol{q^{-1}_{\omega}}

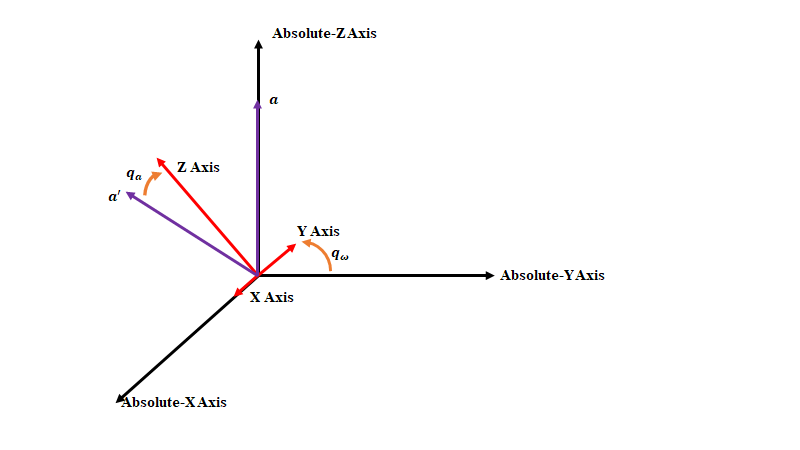
紫矢印が重力加速度のベクトル。センサ軸上では$\boldsymbol{a}$ベクトル。

このとき、$\boldsymbol{q_{\omega}}$に誤差が含まれていない場合、回転後の$\boldsymbol{a^{'}}$の成分は、初期状態の$\boldsymbol{a_{0}}=\boldsymbol{g}=[0,0,1]$と同じになるはずです。

3.誤差を補正するクォータニオンをつくる

しかしながら、実際は誤差が含まれているので、成分は一致しません。
これを一致させるような回転を表すクォータニオン$\boldsymbol{q_{a}}$をつくります。

クォータニオンは回転軸単位ベクトルと回転角でつくることができることは説明しました。

2つのベクトル$\boldsymbol{a^{'}}$と$\boldsymbol{a_0}$の回転軸単位ベクトル$\boldsymbol{n_a}$は、外積を用いることで求められます。

\boldsymbol{n_a}=\frac{\boldsymbol{a^{'}}\times\boldsymbol{a_0}}{|\boldsymbol{a^{'}}\times\boldsymbol{a_0}|}

2つのベクトルの回転角$\theta_a$は、内積を用いることで求められます。

\theta_a=\arccos{(\boldsymbol{a^{'}}\cdot\boldsymbol{a_0})}

この$\theta_a$に、任意係数$\alpha(0<\alpha<1)$をかけたものを使ってクォータニオンをつくります。この$\alpha$が大きければ補正量も大きくなり、小さければ補正量も小さくなります。式(1)より

\boldsymbol{q_a}=\cos{\frac{\alpha\theta_a}{2}}+\boldsymbol{n_a}\sin{\frac{\alpha\theta_a}{2}}

4.クォータニオンを補正する

クォータニオン同士の積はそのまま回転の和になるので、補正後のクォータニオン$\boldsymbol{q^{'}}$は、

\boldsymbol{q^{'}}=\boldsymbol{q_{a}}\boldsymbol{q_{\omega}}

となり、式(3)から計算できます。

ジャイロ+加速度+地磁気で姿勢推定

ジャイロ+加速度だけでも誤差は補正できますが、加速度センサではオイラー角で言うヨー方向の誤差が補正できません。(姿勢を推定する指標になる重力加速度がZ軸=ヨー軸を貫いているため)

ここに地磁気センサを加えることで、ヨー方向の誤差も補正できます。

やることは加速度センサのときと変わりません。
注意することとして、加速度の場合は初期ベクトルがZ軸に貫く重力加速度ベクトルだったので$\boldsymbol{a_{0}}=[0,0,1]^T$でしたが、地磁気の場合は姿勢推定を開始したときの地磁気ベクトル$\boldsymbol{m_{0}}=[m_{x0},m_{y0},m_{z0}]^T$になります。
この初期ベクトルを方位で言う北のベクトルとし、初期クォータニオンをそれに則った値に設定すると、絶対方位におけるセンサの姿勢が得られます。室内ではあまり意味はないですが、屋外でなんか動かすときは方位がわかると便利ですね。

まとめ

いいかんじにセンサフュージョンができた。