Go to Qiita Advent Calendar 2024 Top
LoginSignup
9
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@Talokay(Keitaro Takahashi)

[FFTW] クロスプラットフォーム 対応の FFTWライブラリを使用して高速フーリエ変換を行う

Posted at

最近はWindows, Mac OS, iOSなど、複数のプラットフォームに対応した信号処理プログラムを書く機会が増えたので、クロスプラットフォーム対応のFFTライブラリ、FFTWの使い方をまとめます。

FFTWはフリーソフトウェアでありながら、非常に高速な処理を可能にしているFFTライブラリです。
1次元から多次元のDFTをカバーし、自由なフレームサイズを設定可能なため（効率的な計算は2の累乗にする必要がある）、様々な用途に使用可能です。

開発環境
MacBookPro : macOS High Sierra 10.13.4
Xcode : 9.3.1

#FFTW インストール
Mac OSXのインストール方法は、このサイトがわかり易かった。
http://decafish.blog.so-net.ne.jp/2007-10-06

インストールが無事に完了したら、fftw3.hをXcodeプロジェクトに追加。
さらに、libfftw3.aをBinary Library に追加。（下画像参照）
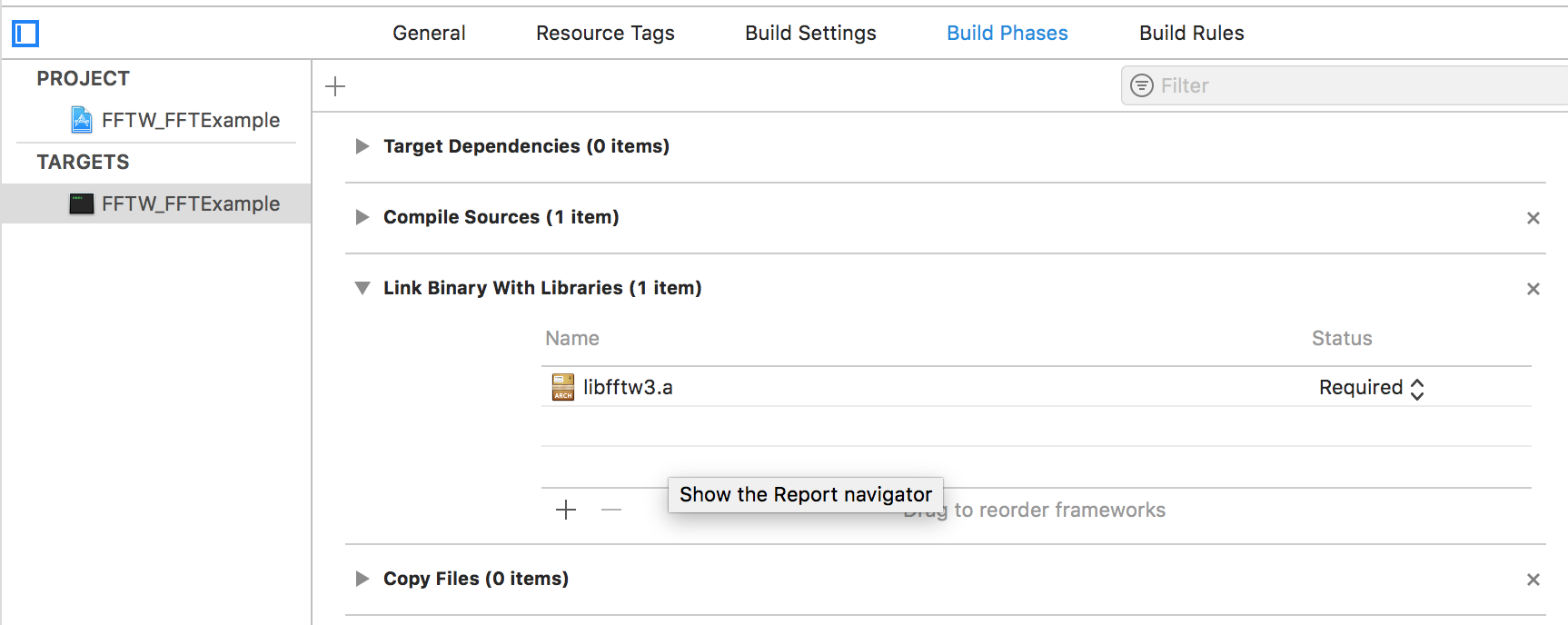
Screen Shot 2018-06-01 at 13.59.40.png

#FFTW Example1

本家のTutorial: http://www.fftw.org/fftw3_doc/Complex-One_002dDimensional-DFTs.html#Complex-One_002dDimensional-DFTs
を参照し、さらにここではサイン波の周波数解析を行う。

  1. fftw2.h を includeする
main.cpp

#include "fftw3.h"

fftwを使用する際は、fftwによって提供されている独自のcomplex型の変数を宣言する。
ここでは、インプットとアウトプットの両方を宣言。

main.cpp
    fftw_complex *in, *out;

fftw_complex型は以下の様にallocateする。

main.cpp
　　const int fftsize = 1024;
    in = (fftw_complex *)fftw_malloc(sizeof(fftw_complex) * fftsize);
    out = (fftw_complex *)fftw_malloc(sizeof(fftw_complex) *fftsize);

使い方としては以下の通り

main.cpp
    int i = frameIndex; // フレームインデックス
    in[i][0] // 実数
    in[i][1] // 虚数

fftwでは、DFT演算を行いために必要なデータを全て格納したplanというデータ型を使用する。

main.cpp
   fftw_plan p;
   p = fftw_plan_dft_1d(fftsize, in, out, FFTW_FORWARD, FFTW_ESTIMATE);

上記はforward FFT の設定方法で、inverse FFT を行う場合は、FFTW_BACKWARDを第四引数に設定する。
第五引数はFFTW_MEASUREかFFTW_ESTIMATEを設定する

FFTW_MEASURE

演算を行うデータ数が複数ある場合、そのデータに最も適したfftsizeを算出して実行する。具体的には、データ毎に異なるfftsizeを使用して、複数回FFTを行い、適切なfftsizeを見つける。FFTW_ESTIMATEに比べて、実行時間が長くかかる。

FFTW_ESTIMATE

FFTW_MEASUREとは対照的に、単純に同じfftsizeを使用して繰り返し計算する。

###実行

DFT演算を開始する際は fftw_execute() 関数にplanデータを渡して実行する。

main.cpp
   fftw_execute(p);

同じ設定で複数回DFTを処理する場合は、この関数のみを繰り返し呼べば良い。

使い終わった後は、メモリの解放を行う。

main.cpp
   fftw_destroy_plan(plan);
   fftw_free(in);

   /* なんらかの処理　*/
   fftw_free(out);

##テスト

サイン波を使用して、DFT演算テストを行う。

main.cpp
    for(int i=0;i<fftsize;i++){
        buffer[i] = sin((float)440.0 / 44100.0 * 2 * M_PI * i);
    }
main.cpp

int main(int argc, const char * argv[]) {

    const int fftsize = 1024;
    fftw_complex *in, *out;
    fftw_plan plan;
    int i;
    
    in = (fftw_complex *)fftw_malloc(sizeof(fftw_complex) * fftsize);
    out = (fftw_complex *)fftw_malloc(sizeof(fftw_complex) *fftsize);
    plan = fftw_plan_dft_1d(fftsize, in, out, FFTW_FORWARD, FFTW_ESTIMATE);
    
    /* create sin wave of 440Hz */
    for(i=0;i<fftsize;i++){
        in[i][0] = sin((float)440.0 / 44100.0 * 2 * M_PI * i);
        in[i][1] = 0.0;
    }
    
    fftw_execute(plan); /* repeat as needed */
    
    fftw_destroy_plan(plan);
    fftw_free(in);
    
    /* get amplitude */
    float amplitude[1024];
    for(i=0;i<fftsize;i++){
        amplitude[i] = out[i][0] * out[i][0] + out[i][1] * out[i][1];
    }
    /* print the result */
    for(i=0;i<fftsize;i++) printf("amplitude[%d] = %lf\n",i,amplitude[i]);
    
    fftw_free(out);
    return 0;
}

##結果

amplitude[0] = 147.694305
amplitude[1] = 153.062424
amplitude[2] = 170.293625
amplitude[3] = 203.283386
amplitude[4] = 260.676941
amplitude[5] = 361.257751
amplitude[6] = 549.621765
amplitude[7] = 951.076660
amplitude[8] = 2034.421875
amplitude[9] = 6898.182617
amplitude[10] = 222777.671875
amplitude[11] = 17526.615234
amplitude[12] = 3474.977783
amplitude[13] = 1466.198853
amplitude[14] = 815.296509
amplitude[15] = 523.652100
amplitude[16] = 367.454102
amplitude[17] = 273.715393
amplitude[18] = 212.828400
amplitude[19] = 170.907669
amplitude[20] = 140.726440
Screen Shot 2018-06-01 at 14.43.39.png

fftのbinから周波数を求めるやり方は以下

binIndex * 44100.0 / fftsize (0 <= binIndex < fftsize)

よって、ピークの周波数は430.66Hzとなる。

この時、隣り合うbinの強度を参照して重心を求めることで、より正確な値を算出できる。

    float freq = 44100.0 / float(fftsize);
    float freq_accum = amplitude[9] * 9 * freq;
    freq_accum += amplitude[10] * 10 * freq;
    freq_accum += amplitude[11] * 11 * freq;
    
    float amp_accum = amplitude[9] + amplitude[10] + amplitude[11];
    
    float fixed_freq = freq_accum / amp_accum;

私はこのやり方をずっとやっていたが、メジャーなやり方は、隣会う数値から放物線を計算して、その頂点を求めるらしい。

結果は 432.516Hz
精度はあまり高くない。

##原因

生成したサイン波の始まりは０スタートだが、０終わりになっていないので、波形に歪みが生じている。

sin[0] = 0.000000
sin[1] = 0.000001
sin[2] = 0.000005

sin[7] = 0.000196
sin[8] = 0.000290
sin[9] = 0.000408 // 0じゃない！

##窓関数

窓関数を使用する場合は以下の通り。

hanning window

main.cpp
   /* create sin wave of 440Hz */
    for(i=0;i<fftsize;i++){
        in[i][0] = sin((float)440.0 / 44100.0 * 2 * M_PI * i) * (0.5 - 0.5 * cos(2 * M_PI * ((float)i/fftsize)));
        in[i][1] = 0.0;
    }


amplitude[0] = 0.003741
amplitude[1] = 0.004732
amplitude[2] = 0.008512
amplitude[3] = 0.018578
amplitude[4] = 0.046741
amplitude[5] = 0.138677
amplitude[6] = 0.522167
amplitude[7] = 2.904061
amplitude[8] = 34.940998
amplitude[9] = 7698.087891
amplitude[10] = 61670.855469
amplitude[11] = 28713.363281
amplitude[12] = 174.219727
amplitude[13] = 7.470490
amplitude[14] = 1.039181
amplitude[15] = 0.240988
amplitude[16] = 0.075089
amplitude[17] = 0.028418
amplitude[18] = 0.012351
amplitude[19] = 0.005954
amplitude[20] = 0.003112
Screen Shot 2018-06-01 at 14.46.29.png

ピークと、前後のbinの値を元に重心を計算すると、結果は

439.892Hz

かなり近くなった！

9
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
9
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?