1. 過学習
学習用データに特化してしまって、検証用データをつかうと、正解率があがらないどころか悪化する状態を過学習といった。学習のエポックが進めば進むほどに、学習データに特化して、検証データを使うと、どんどん正解率が悪化していく。
ちなみに、入力値が小さいのに、ネットワークのノード数が多すぎる場合、過学習が起きやすい。大きいものを最適化するためには、多くのデータが必要ということである。
では、どうやったら過学習を防ぐことが出来るか。
基本的な方法は、
NNの自由度を下げてやる。その手法は、正則化である。
- L1正則化、L2正則化
- ドロップアウト
ドロップアウトはちょっと違うが、ある意味正則化の一つ。
2. L1,L2正則化
2.1 過学習の状態、原因
過学習状態のモデルというのは、ある重みが大きすぎる状態になっている。少ない入力値を過大評価しているのである。ほかの入力値(検証データ)が入ってきたときに対応が出来ない重みの状態。
2.2 過学習の回避策
誤差逆伝搬法にて学習を行って最適な重みを求めるわけであるが、この際の計算に、誤差だけでなく、正則化項もつけてやることで、大きすぎる重みが出来ることを抑制することが出来る。
2.3 pノルムによる正則化
では、具体的に正則化項とは、何かというと、機械学習のときに勉強したL1ノルム(マンハッタン距離)、L2ノルム(ユークリッド距離)のことである。
Loss = E_n (W) + \frac{1}{p} \lambda ||x||_p \\
※ \lambda は、ハイパーパラメータ
p=1の場合が、L1ノルムによる正則化(Lasso回帰)
p=2の場合が、L2ノルムによる正則化(Ridge回帰)
である。
そして、上記の式にある正則化項 $||x||_p$は、実際には各中間層の重み$w$を使うので、以下のようになる。
||w^{(1)} ||_p = ( |W_1^{(1)}|^p + \cdots + |W_n^{(1)}|^p )^{\frac{1}{p}} \\
||w^{(2)} ||_p = ( |W_1^{(2)}|^p + \cdots + |W_n^{(2)}|^p )^{\frac{1}{p}} \\
||x||_p = ||w^{(1)} ||_p + ||w^{(2)} ||_p
上記のネットワークでL1ノルムで正則化するなら
||w^{(1)} || = ( |W_1^{(1)}| + \cdots + |W_n^{(1)}| ) \\
||w^{(2)} || = ( |W_1^{(2)}| + \cdots + |W_n^{(2)}| ) \\
||x||_1 = ||w^{(1)} || + ||w^{(2)} || \\
E_n (W) + \lambda ||x||_1 \\
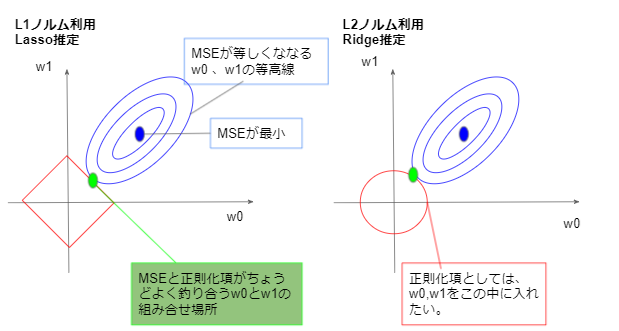
2.4 L1,L2ノルムによる正則化の違い
L1ノルムとL2ノルムを使って誤差関数を正則化した場合、L1ノルムの方は、最適値を求めた際に重みがスパース化される。(重み0の場所が発生し、特徴をよく表す)
詳細は下記参照。
2.5 pノルム正則化の問題
ノルム正則化は、誤差関数に追加で不要なものを足していることになるので、もともとの純粋な誤差関数の最適解にはたどり着けなくなってしまうという問題がある。
例えば、学習用データで100点の正答率だったものが、正則化を行うと、80点に下がるという状態。
3. ドロップアウト
ドロップアウトとは、中間層のノードをランダムに削除して学習を行うことで、データのバリエーションが増えたように見せる手法である。単純だけど効果が高い。
なお、この結果、学習に時間がかかるという問題が発生する。なかなか最適解に辿り着かない。