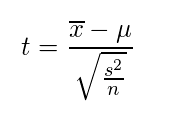仮説検定 ~1標本の検定(標本平均)~

はじめに

現在、絶賛統計検定2級を勉強中のものです！統計ってイメージつかめても実際に応用するとなると分からないみたいなことが多いです。
なので、アウトプットを作って知識の定着を目指していきます！。
今回は1標本の母平均の検定をしていきたいと思います。

仮説検定とは

その前に今回初めて仮説検定について書くので、統計検定2級のテキストより仮説検定について要約します。

仮説検定とは正確には統計的仮説検定と呼ばれる。
データをもとに仮説が正しいかどうかの考察を統計的にするものである。

用語の意味

• 帰無仮説

「差がない状態」を表す仮説(H0)。例えば μ = 0 など、何かの数値と＝になっていると表す。
得られた値(標本平均、不偏分散など)が帰無仮説の下で(帰無仮説が従う確率分布の下で)、どれほど珍しい値なのかを裾の確率を用いて検定する。

• 対立仮設

帰無仮説が棄却されるときに採択される明示的に書かれた仮説(H1)。対立仮説は「差がある状態」を表す。例えば μ ≠ 0 や μ > 0 などと表される。
対立仮説の書き方で両側検定か片側検定と検定方法が異なる。

• 有意水準

帰無仮説をどの確率α以下が出たら棄却すると決めるしきい値。本当は帰無仮説が正しいのに対立仮説を採択する確率がα以下と言える。
帰無仮説が受容された場合は正しい(誤り)の確率がないため、帰無仮説が正しいとは積極的には言えない。
α点以下を棄却域、それ以外を受容域と呼ぶ。

• 片側対立仮説両側対立仮説

両側は μ ≠ 0 と片側は μ > 0 or μ < 0 などと書かれる。
明確に何に対しての検証だから、この仮説とは決まっていない。証明したいことをもとに仮説を立てる。
片側と両側では有意水準の値が異なる。有意水準5%であれば、
片側は検定統計量(z値など)が μ < 0 であれば下側5%以下かを見て μ > 0 であれば 上側5%以下かを見る。
両側は検定統計量が μ ≠ 0 では 上側と下側が 0.05/2= 0.025 = 2.5%以下かを見る。

検定の手順

• 帰無仮説と対立仮説を立てる
  • 対立仮説から片側か両側かを決める
• 有意水準を決める
  • 通常、1%や5%がよくつかわれる
• 帰無仮説をもとに検定統計量の確率を求める(P値)
  • 標準正規分布表やt分布表などを用いて、裾の確率を求める
• 有意水準を下回るかどうかを見る
  • 結果によって帰無仮説を受容するか棄却するかを判断する
• 区間推定を行い統計量の分布を推測する

要するに帰無仮説をもとに統計量の裾の確率が何%かを見て、帰無仮説を棄却するか決める！と言った感じです！
(まだ2級の範囲なので甘いところあるかもですが、ご了承ください。。。)

Pythonで検定してみた

頭で理解してるだけじゃもったいない！ということで、pythonでコードを書いてみました。

問題はこちらです。

某ハンバーガーチェーン店のナゲットは一つ20gと言われています。これが本当に20gなのか、ナゲットを10個買い標本平均を取り調べてみる。
帰無仮説(H0) : μ = 20
対立仮説(H1) : μ ≠ 20
サンプル数 : 10
観測値　　　 : [20.0, 28.3, 20.5, 22.0, 25.8, 31.9, 18.8, 30.0, 23.0, 23.1]
標本平均　　 : 24.3
不偏分散　　 : 20.0
(架空のデータです。)
ナゲットの母平均と母分散は正規分布に従っていると仮定して仮説検定を行う。

問題から分かる通り、今回は1標本の母平均の検定を行っていきます。
母分散が既知の場合は z値を求めて z検定し、

母分散が未知の場合はt値を求めてt検定します。

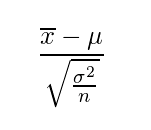
pythonのscipyライブラリでは観測値を渡すことで、簡単に検定をすることができます。
今回は母分散がわからないと仮定しているので、 t検定を行います。↓を用いる。

pythonコードではこの求めた t値の裾の確率(P値)を求めて検定を行います。手計算だと分布表では難しい場合があるので t値を使い調べる。

from scipy import stats
import numpy as np

# 適当なデータを準備
naget_samples = [20.0, 28.3, 20.5, 22.0, 25.8, 31.9, 18.8, 30.0, 23.0, 23.1]
u = 20
result = stats.ttest_1samp(naget_samples, u, alternative="two-sided")
ci = result.confidence_interval(confidence_level=0.95)

# 0.025で有意か確認をする
ish1 = np.sum(result.pvalue < 0.05)

if ish1:
  print(
      f"""
        P-値 : {result.pvalue} なので
        有意水準5%で帰無仮説は棄却される

        95%信頼区間 : {np.round(ci.low,1)}, {np.round(ci.high, 1)}
      """
  )
else:
  print(
      f"""
        P-値 : {result.pvalue} なので
        有意水準5%で帰無仮説は採択される

        95%信頼区間 : {np.round(ci.low,1)}, {np.round(ci.high, 1)}
      """
  )

output

        P-値 : 0.013394467973091498 なので
        有意水準5%で帰無仮説は棄却される

        95%信頼区間 : 21.1, 27.5

stats.ttest_1samp(naget_samples, u, alternative="two-sided")
このコードで観測値のデータ(array like)、 と帰無仮説でのμの値、両側検定と指定しています。
結果は簡単に出ました。
また、result.confidence_interval(confidence_level=0.95) から引数の信頼区間を求めることができます。
信頼区間は真の分布の推測に役に立つので求める必要があります。

標本平均の t値を求める式を使った計算でも、t = 3.06...で t(9) = 2.262(α=0.025の時)で 3.06 > 2.262 なので帰無仮説を棄却できることが分かります。

さいごに

Pythonを使うことで超簡単にt検定が実装出来ました。
ただ、やっぱり実装してみないと分からないことが多いので、頭で理解したら即python書くみたいにしていきたいですね。今後も統計学んだらpythonで実装をしてみます！
(あと、より分かりやすい説明ができるようにする)

p.s 他に説明必要な単語はまた追加で説明を入れる…！