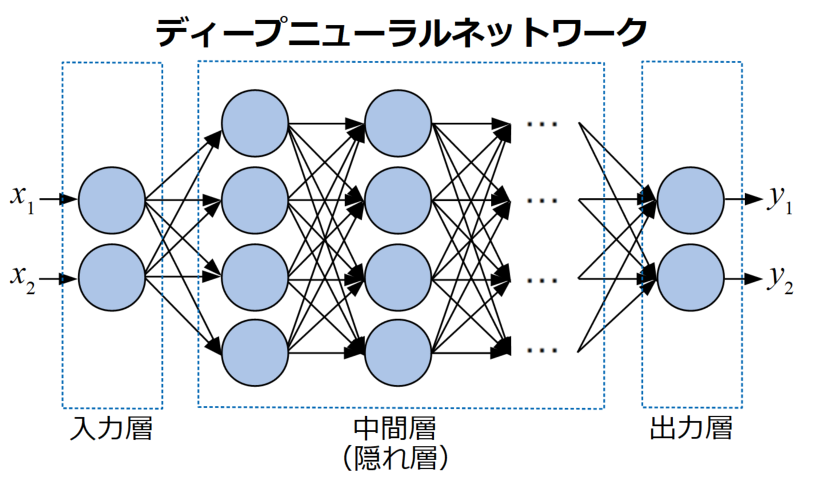
こんにちは!機械学習を勉強している初心者エンジニアです。今回から機械学習のアルゴリズム(特にディープラーニング)の理解に必要な数学の紹介・解説を行っていきたいと思います!Pythonを使いながら文系の方でも理解できるように作っていきます!理解できなかったところ、筆者の解釈の間違いありましたらコメントお願いいたします![]()
今回は線形代数のスカラーとベクトルと行列について解説していきたいと思います!
これは機械学習のアルゴリズムを理解するのに必須の知識です。また、ベクトルや行列の計算はプログラムを書く際でも役立つ知識になります。例えば、データフレームを扱うときは行列計算を知っていると助けになります。
それでは実際にpythonを使いながら説明していきます。
スカラー、ベクトル、行列について
まずは簡単にスカラーとベクトルと行列の説明をします。
スカラー
スカラーとは「大きさの性質のみを持つ数値」です。つまり単なる数値ですね。これは説明不要ですね。
# スカラー
scaler = 3
print('Scaler: ', scaler)
Scaler: 3
ベクトル
ベクトルとは「向きと大きさを持つ量」です。少しわかりにくいですが、言葉で簡単にいうと矢印の方向に進む量を表しています!
プログラム上のベクトルの形と2次元グラフのベクトルを書いてみます!
# ベクトル
vector = np.arange(1, 6)
print('Vector: ', vector)
# ベクトルの描画
plt.quiver(0,0,3,2, angles='xy', scale_units='xy', scale=1)
plt.text(3,2, '[3, 2]', color='red', size=15)
# ラベル
plt.xlabel("x", fontsize=16)
plt.ylabel("y", fontsize=16)
# x軸とy軸
plt.axhline(0, color="gray")
plt.axvline(0, color="gray")
# リミット
plt.xlim(-3,3)
plt.ylim(-3,3)
plt.grid()
plt.show()
Vector: [1 2 3 4 5]
↑5次元配列
上記のようになりました。ベクトルは特定の位置(この場合は原点)からの方向と大きさを表すものというのがわかりますね。
また、普通参考書や図ではベクトルは次のように表されます。
x=\left(\begin{array}{c}x_{1}\\x_{2}\\x_{3}\\.\\x_{n}\end{array}\right)
x=(x_{1},x_{2},x_{3}...x_{n})
\overrightarrow{ab}
または
X
などで表されます。なんでこんな形になるとかは使っていくうちにわかると思います。
まずはこんな形が出たらベクトルだと思ってください!
ベクトルのいろいろな計算
ベクトルとは何だというのは理解できたと思うので、ベクトルの求め方、ベクトル同士の計算などをみていきたいと思います。この計算は機械学習の理解において必須ではないですが、プログラムを書く際に役に立ちますので軽く説明していきます。
※ベクトルは線形性の性質を持つので、何次元に拡張されようが計算方法は変わらず計算量のみ増えるので、見てわかりやすい2次元で全て説明していきます。
ベクトルの求め方
2地点A,Bがグラフ上に置かれているとき、三平方の定理を使うことでベクトルを求めることができます。
先ほど使ったベクトルの図を使ってみましょう。
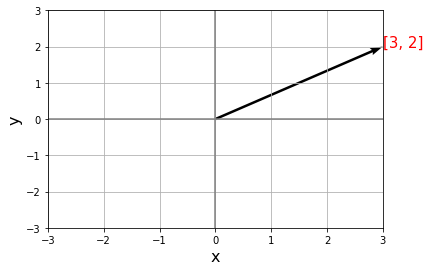
この図から2点、(0, 0)と(3, 2)があるのがわかります。そしてこのように直角三角形が描けるのがわかります。
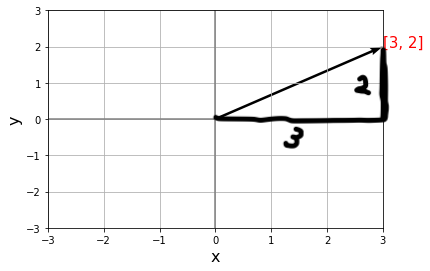
三平方の定理とは2辺の長さがわかるときそれ以外の1辺の長さがわかるというものです。
なのでベクトルは次の式で求めれます。
c=\sqrt{a^{2}+b^{2}}
この図で言うと
c=\sqrt{3^{2}+2^{2}}
となります。
2つのベクトルの和と差と距離
ベクトルの和と差は単純に長さの合計と長さの差となります。なので式はとてもシンプルです。
ベクトルの和:
C=A+B=(a_{1}+b_{1},a_{2}+b_{2})
ベクトルの差:
C=A-B=(a_{1}-b_{1},a_{2}-b_{2})
非常にシンプルな式となりました。単純な足し算引き算ですね。
ここで小文字のa,bなどでてきてますが、これは「成分表示」されている状態です。ベクトルAを2次元のベクトルと考えると2点であらわせれると言うのはわかると思います。ベクトルは下記のようにあらわせれます。ベクトル同士の色々な計算は同じ方向の成分同士を計算することでできます。
A=a_{1}+a_{2}
次に距離でベクトル同士の距離を計算することができます。distanceの公式を使うことで求めれます。
d=|A-B|=\sqrt{(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}}
ベクトルの内積
ここの知識は勾配降下法の理屈を理解するのにとても役に立つと思います。式は以下の通りです
A*B=a_{1}b_{1}+a_{2}-b_{2}
これも次元数が増えても変わりません。
同じ方向の成分をかえて合計するだけです!
三角関数を使ってベクトルの内積の特徴をみてみましょう。(スライドの画像となります)
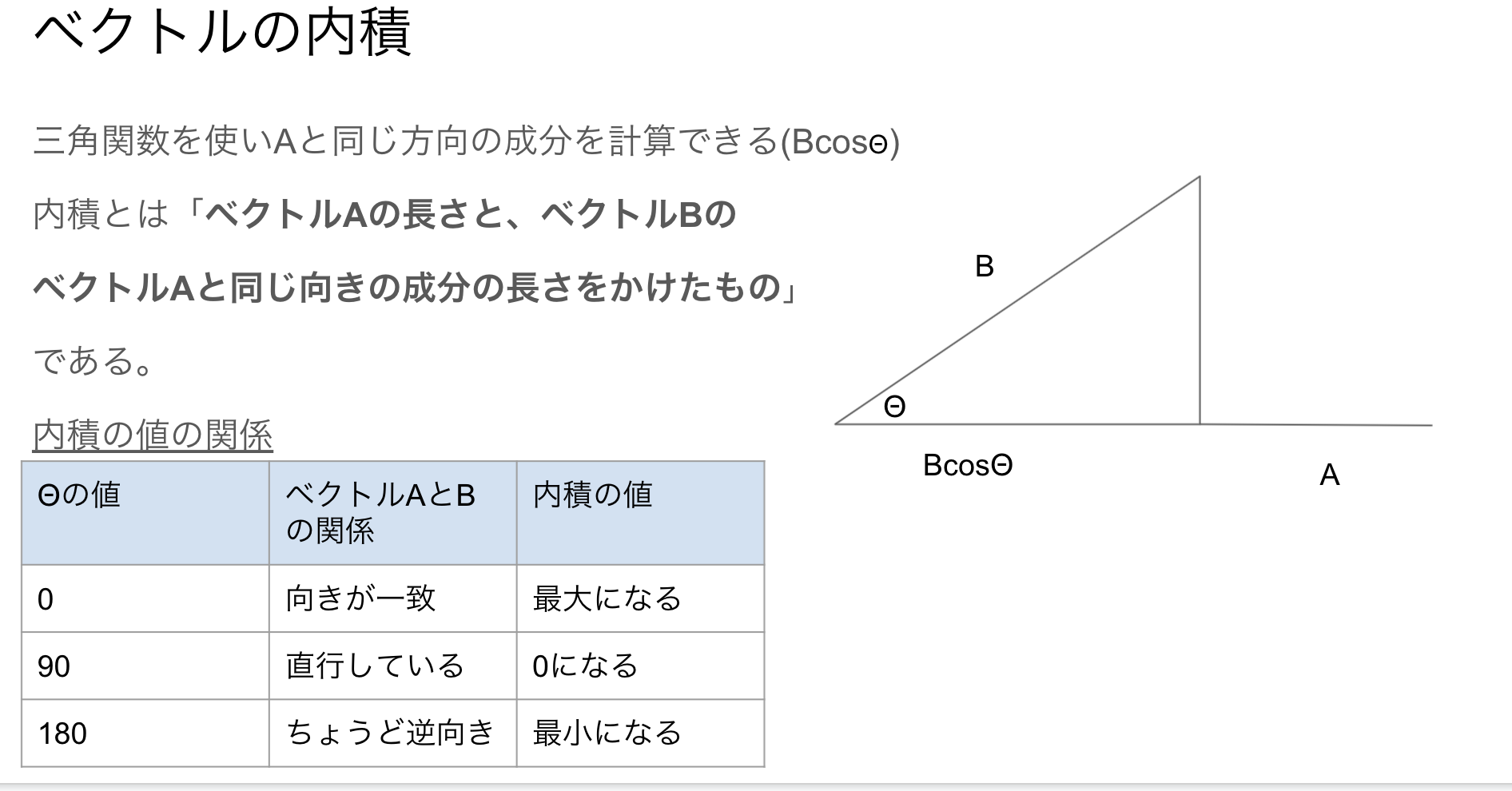
書いてある通り、内積は同じ方向の成分をかけること、つまり「ベクトルAの長さと、ベクトルBの
ベクトルAと同じ向きの成分の長さをかけたもの」なので上記のように表すことができます。式は下記となります。
A*B=|A||B|\cos\theta
そしてcosの特性を利用することで、内積の値が最大か0か最小になることがわかります。
これは後々説明する勾配降下法で役に立つ知識なので押さえておきましょう!
それでは最後にまとめてpythonで計算をしてみましょう!
# ベクトルの色々な計算
p1 = (0, 0)
p2 = (4, 3)
vector1 = np.array([2, 4])
vector2 = np.array([3, 5])
# 三平方の定理を使ってベクトルを求める
c = np.sqrt((p1[0]+p2[0])**2+(p1[1]+p2[1])**2)
print('vector: ', c)
# ベクトルの和と差
add = vector1 + vector2
diff = vector2 - vector1
print('add: ', add)
print('diff: ', diff)
# ベクトルの距離
distance = np.linalg.norm(vector1-vector2)
print('distance: ', distance)
# ベクトルの内積
dot = np.dot(vector1, vector2)
print('dot: ', dot)
vector: 5.0
add: [5 9]
diff: [1 1]
distance: 1.4142135623730951
dot: 26
行列
行列(マトリックス)とは値を縦と横に矩形状に配列したものです。図で表すとこんな感じです。
\begin{bmatrix}w_{11} & w_{12} \\w_{21} & w_{22} \end{bmatrix}
また単位行列と呼ばれるものもあります。単位行列とは左から右にかけての対角線の値が「1」でそれ以外が「0」の値を持つ行列です。ディープラーニングでは勾配降下法(次回以降説明します)を使っての学習を最適化するために初期値の重みの値を単位行列にすることがあります。
図で表すとこんな感じです。
\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix}
pythonで普通の行列と単位行列の作成をしてみます。
# 行列の作成
# 2x2の行列
matrix = [[0, 1], [2, 3]]
print('普通の行列:\n', np.array(matrix))
# 0の値の行列
zero_matrix = np.zeros((2,2))
print('\n0の行列:\n', zero_matrix)
# 単位行列
e_matrix = np.eye(2,2,k=0)
print('\n単位行列行列:\n', e_matrix)
普通の行列:
[[0 1]
[2 3]]
0の行列:
[[0. 0.]
[0. 0.]]
単位行列行列:
[[1. 0.]
[0. 1.]]
行列の生成方法は他にもまだまだあります。興味ありましたら調べてみてください。ここで大事なのは行列とはpythonで言う2次元配列のことを指すと言うことです!
ベクトルx行列の計算
これは公式の理解に必須の知識となっています。みなさんお馴染みのグラフの式y=ax+bがあると思いますが、それを拡張したのがニューラルネットワークなのです。aとbはWに置き換わり表現されています。ここではまだDLに入る前の段階なので詳しく上げません。下記の図を見てこの計算はベクトルと行列の計算なんだなと思っていてください!
では本題に入ります。ベクトルと行列の積では列番号が同じところがかけらるので、列数が一緒じゃないと計算ができません。
\begin{bmatrix}w_{11} & w_{12} \\w_{21} & w_{22} \end{bmatrix}*\left[x_{1},x_{2}\right] = \begin{bmatrix}w_{11}x_{1} & w_{12}x_{2} \\W_{21}x_{1} & w_{22}x_{2} \end{bmatrix}
各ベクトルの値が対応する列でかけられているのがわかりますね。
pythonでも書いてみましょう!他の計算も書いておきます。
vector = np.arange(1, 3)
matrix = np.array([[0, 1], [2, 3]])
print('使用するベクトル: ', vector)
print('使用する行列:\n', matrix)
# ベクトルx行列
print('\nvector*matrix:\n', vector * matrix)
# ベクトルxベクトル
print('\nvector*vector:\n', vector * vector)
# ベクトルxベクトル
print('\nmatrix*matrix:\n', matrix * matrix)
使用するベクトル: [1 2]
使用する行列:
[[0 1]
[2 3]]
vector*matrix:
[[0 2]
[2 6]]
vector*vector:
[1 4]
matrix*matrix:
[[0 1]
[4 9]]
まとめ
以上でベクトルと行列の解説は終わりです。理解してしまえばすごく簡単だと思います!ベクトルと行列はプログラムを書いていく上で有用な知識になると思いますのでぜひマスターしましょう!今回特に大事なのはベクトルx行列とベクトルの内積です!内積ではベクトル間の角度で内積の値が変動することをぜひ覚えてください。ベクトルと行列の計算もディープラーニングでは必須ですのでこれも押さえましょう!
指摘やわかりにくいと言った場合はコメントお願いいたします。
次回は微分とちょっと積分をします!