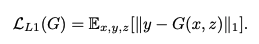はじめに
ポケモンのタイプって結構見た目で大方分かったりすることありますよね？以前Qiitaでディープラーニングは未知のポケモンのタイプを予測することができるのか？という記事でも触れた話題ですが、今回はこのポケモンのタイプについて、深堀していきたいなと思います。具体的にはとあるAタイプポケモンがもしBタイプポケモンだった場合、こんな感じのデザインになるよね！って画像をCycleGANを使って再現できるかどうかを試してみようと思います。
タイプ毎カラー分布の違い
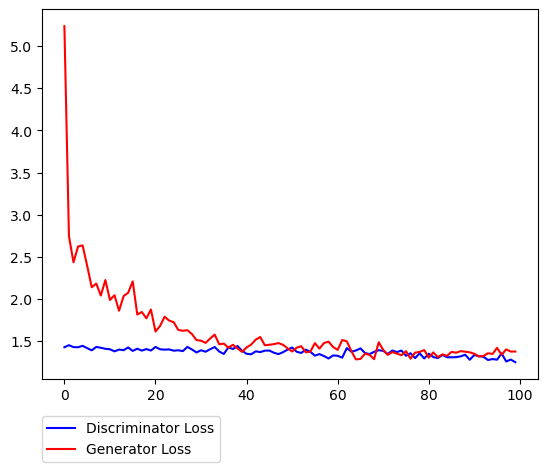
まず、問題設定としてタイプ毎にある程度、見た目の特徴が存在しないと、機械学習タスクとしては落とし込めません。そこでタイプ毎に色の分布がどの様になっているのか、RGB成分を3Dプロットして確認してみました。GitHubには全タイプの結果を載せていますが、以下では炎、水、草タイプの結果を示してみます。
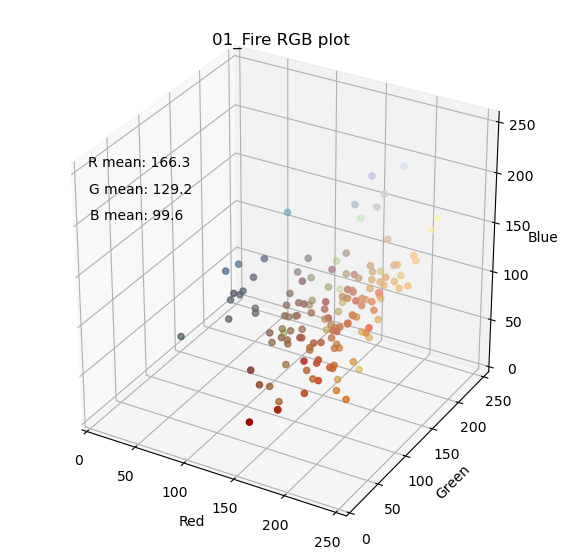
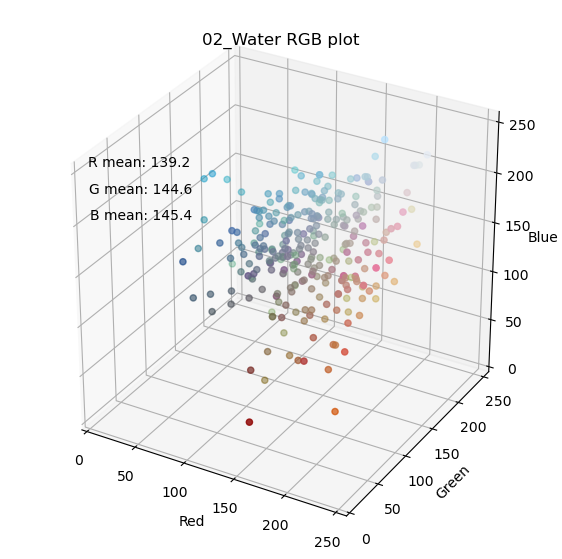
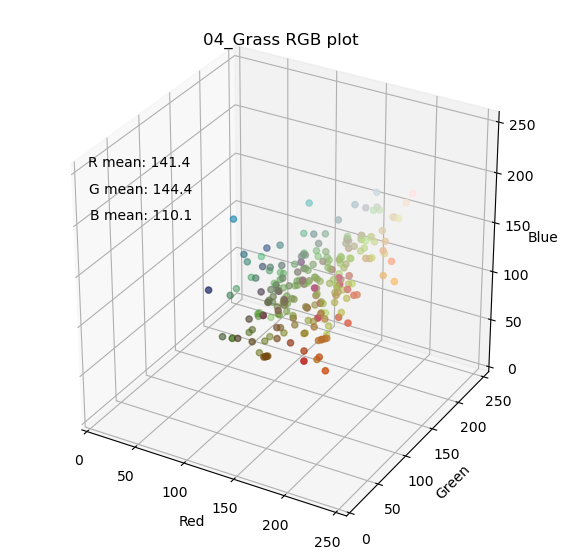
それぞれの点が1体のポケモンの特徴点になります。座標はそのポケモンの平均画素値(R, G, B)です。尚、今回は背景の白(255, 255, 255)、及び黒（0, 0, 0）を除外した平均値を計算しています。また、それぞれの点のカラーがそのポケモンの平均画素になります。見たところ、炎タイプ（赤）、水タイプ（青）、草タイプ（緑）という傾向はなんとなく現れている様に感じます。
また、下記画像は代表的な御三家ポケモンのHSVヒストグラムを凝って表示している図になりますが、やはりその傾向は確認できるかなと思います。
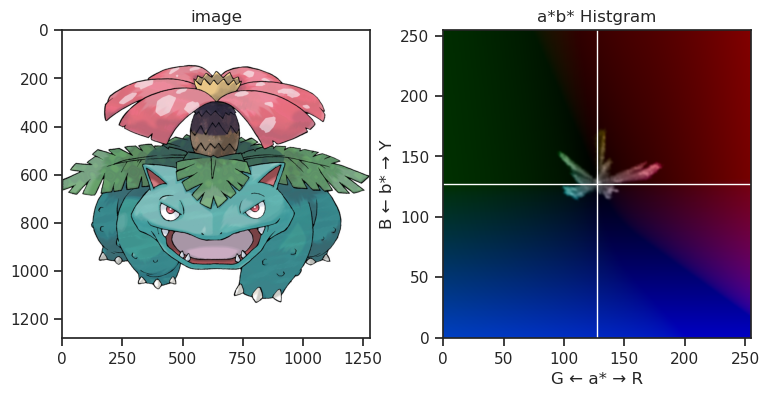
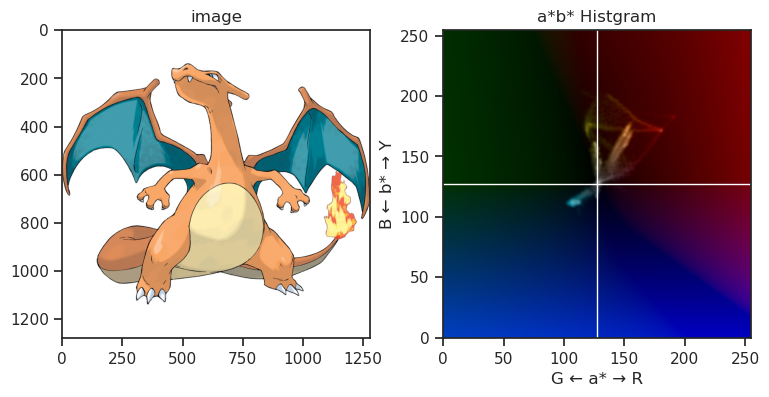
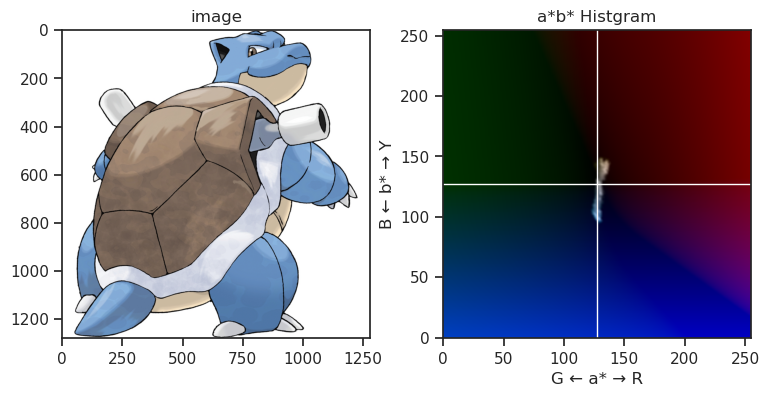
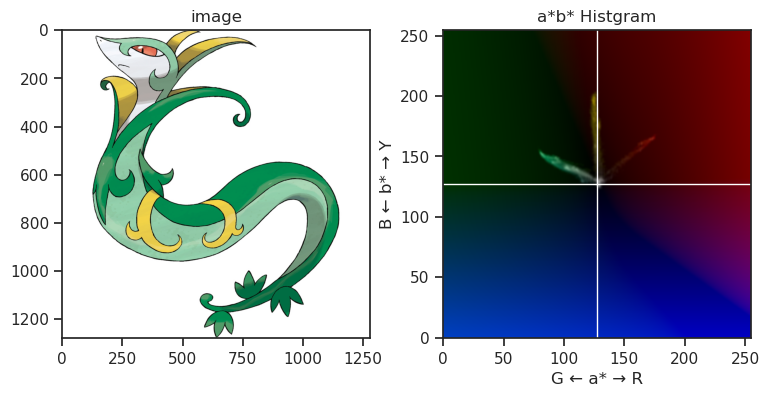
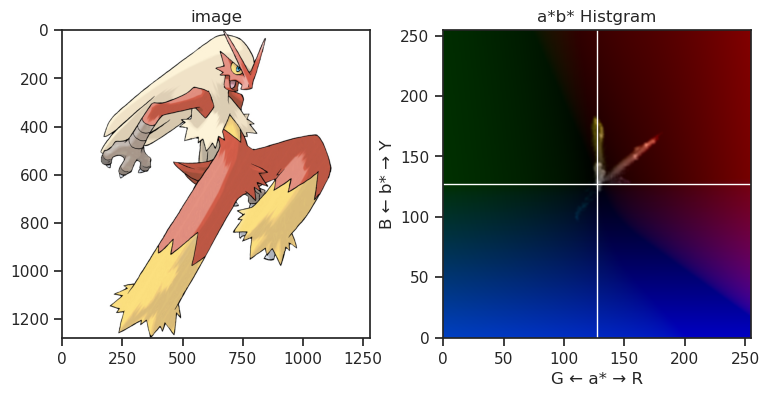
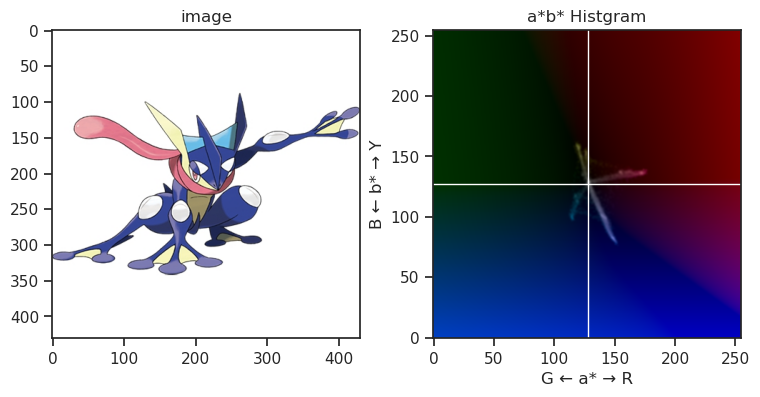
CycleGANの概略
Image to Image
馬の画像をシマウマに、シマウマの画像を馬に変換する有名なあれです。この前Qiitaでpix2pixの実験についてのブログを書きましたが、CycleGANもpix2pixと同じ、Image to Image のGANになります。有名なDCGANなどはノイズ -> Imageですが、こちらはImage -> Imageになります。
pix2pixとの比較
pix2pix
pix2pixは以下の様にinputと教師データがペアの関係性にある様なデータセットにおいて、活用できるGANになります。構造上、通常の教師あり学習の要素も大きく、学習結果も安定しています。
非常に使い勝手の良い万能なGANですが、ペアとなるデータセットを集めること自体が困難であることが欠点になります。
Image-to-Image Translation with Conditional Adversarial Networks [[arxiv]] (https://arxiv.org/pdf/1611.07004.pdf) より出典
pix2pixの損失関数は以下の2つです。一つ目はGANでお馴染みの Adversarial Loss です。
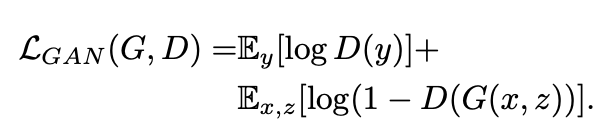
機械学習をやっていると最早定番と言える Binary Cross Entropy をベースとしています。もう少しわかりやすく書くと、
math D:loss = -\sum_{i=1}^{n}\bigl(t_ilogy_i - (1-t_i) log(1-y_i) \bigl)
要はtarget=1の時はその出力をできるだけ高く(最終層にsigmoidかますので、大きければ大きいほど1に近く)。target=0の時はその出力を負の方向に大きくするように訓練すれば、ロスが小さくなる感じです。
逆にGについては上式を最大化させる様に訓練することになります。更にGの場合自ら生成した偽画像しか評価されないため、上式の左項が消えて、よりシンプルになります。
math G:loss = \sum_{i=1}^{n}log\Bigl(1 - D\bigl(G(z_i))\bigl) \Bigl) （最大化）\\ = \sum_{i=1}^{n}log\Bigl(D\bigl(G(z_i)) - 1\bigl) \Bigl) （最小化）\\ = -\sum_{i=1}^{n}log\Bigl(D\bigl(G(z_i))\bigl) \Bigl) (これを最小化させると捉えることも可能)
尚、Adversarial Lossのそもそものモチベーションは分類器（Discriminator）を上手く騙せる様な、Generatorを生成していくことなので、分類モデルで使われるロス（よくある例だとHingeLossなど）をBCEの代わりに使用する事もあります。特にBCEの場合、どうしても損失が収束しづらい事もあり、GANの学習に Hinge Loss を使用することはありがちなテクニックの一つになっています。(Cross entropy loss と Hinge loss)
pix2pixの二つ目のロスは凄く単純で教師データとoutputのピクセル間距離になります。例えば下記はL1 Loss（ピクセル同士の差の絶対値）になります。このロスのモチベーションはGeneratorのoutputと教師データの分布を近くすることにあるため、ピクセル同士のL1距離以外にもMSE(Mean Absolute Error)などをロスとして使用する事もあります。
CycleGAN
CycleGANはpix2pixと異なり、2つのGeneratorと2つのDiscriminatorが存在します。前段で、CycleGANの学習にはペアを作る必要がなく、適当に集めた馬の画像群と適当に集めたシマウマの画像群を揃えれば学習可能と書きましたが、一つ目のGeneratorが馬 -> シマウマ。もう一方のGeneratorがシマウマ -> 馬の変換を行います。そしてそれぞれのGeneratorに対してDiscriminatorが存在するので、合計4つのネットワークを同時に学習させていくことになります。
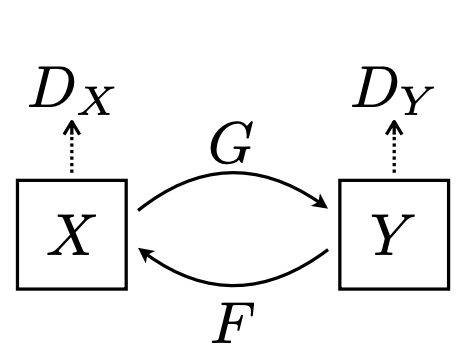Unpaired Image-to-Image Translation
using Cycle-Consistent Adversarial Networks [[arxiv]] (https://arxiv.org/pdf/1703.10593.pdf) より出典
CycleGANには以下の3つのロスが存在します。
Adversarial Loss
先ほどのpix2pixと同じです。pix2pixと異なる点ですが、CycleGANの場合、G-Dのペアが2つ存在するため、そのロスも2つ取らなければならない点です。
Cycle Consistency Loss
これがpix2pixと大きく異なる Cycle GAN の面白い特徴になります。
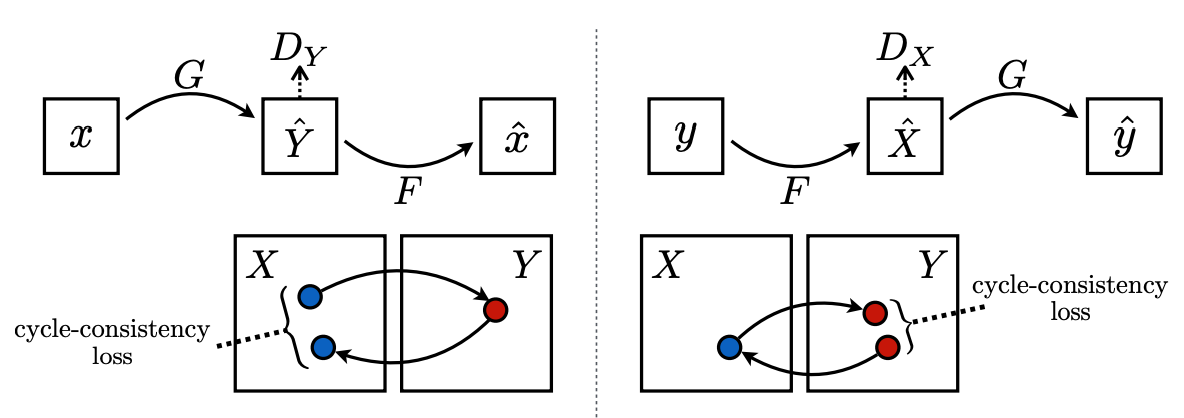
Unpaired Image-to-Image Translation
using Cycle-Consistent Adversarial Networks [[arxiv]] (https://arxiv.org/pdf/1703.10593.pdf) より出典
X（馬画像群）からあるデータ $x$ を取り、Generator G（馬画像をシマウマ画像に変換するGenerator）で変換後、さらにその画像をGenerator F（シマウマ画像を馬画像に変換するGenerator）で変換します。この二回変換後の画像を $x'$ とした場合、$x$ と $x'$ ピクセル間の差の絶対値をロスとします。そして、その全く逆の事も行います。（図の右側）
ある画像をGenerator二回挟んで行って来いした時、元どおりの画像により近い画像が生成できる様に二つのGeneratorを学習させていくことになります。
Identity Mapping Loss
こちらは元論文において、あってもなくても良いかも議論がされていますが、一応今回の実装では使いました。X（馬画像群）からあるデータ $x$ を取り、Generator F（シマウマ画像を馬画像に変換するGenerator）で変換した画像データを $x'$ とした場合、$x$ と $x'$ ピクセル間の差の絶対値をロスとします。Cycle Loss同様、その全く逆も行います。
ドメインXの画像をGenerator（Y -> X）に突っ込んだ場合において、出てくる結果と元画像が近しければ近しいほど、そのロスは小さくなります。
結果
以下、簡単ですが結果になります（左: original, 右: color changed）。尚、学習に使用したポケモン画像（train）と、下記に示しているポケモン画像（valid）に被りがない様、KFoldでデータを切っています。
画像データはKaggleから拝借させて頂きましたが、やはり枚数自体は少なく各タイプとも200枚強とかなり少ない数での学習になっています。GCP料金の関係上、エポック数も少なく、あまりこれといった工夫も今回は行っていないので、データの量、及び工夫次第でもっと良い結果になる可能性はあるかなと思います。
Water -> Grass
Water -> Fire
Grass -> Water
Fire -> Water
Loss（水 <-> 草）
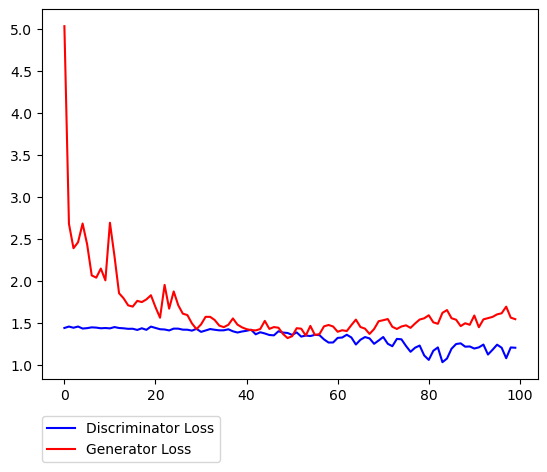
Loss（水 <-> 炎）
序盤は、Cycle LossやIdentity Lossが大きく下がっている影響でガクンとGeneratorのロスが下がり、その後は良い感じで拮抗している様子が伺えます。結果画像に関しては特に 青 <-> 緑の変換が特に上手く行ってる気はします。（元々のデータ分布の影響も多分にあると思っています）。
まだできていませんが、他タイプも時間あるときに試してみたい。