More than 5 years have passed since last update.

HDNNPのMPNNsによるGCNNとしての一般化

Posted at 2019-11-14

1. High‐Dimensional Neural Network Potentials (HDNNP)^[1]

　HDNNPはJörg Behlerらによって開発された、系のエネルギーを算出する機械学習ポテンシャルの一つである。系のエネルギーを計算することが可能となれば、分子力学法(MM)や分子動力学法(MD)、モンテカルロ法などによってその系の熱力学的特性などを知ることができる。

既往手法

　このエネルギーを計算する方法としてはほかに、古典力場（力場　Force field:FF)のような経験に基づくポテンシャルや、密度汎関数法(Density Functional Theory:DFT)のような第一原理計算（経験的なパラメータを用いず、理論にのみ基づく計算）をもちいてエネルギーを計算する方法が用いられている。それぞれの方法については、省略します。ただし、特徴として

	古典力場	DFT
精度	特定の系に最適化されている	精度が高い
速度	早い	非常に遅い
許容サイズ	1万近くまでよく行われている	百数十程度

のように、DFTでは精度が高いものの時間スケールでも空間スケールでもかなり小さなものしか取り扱えないことがわかる。

Neural Network Potentials: NNP の目的

古典力場が高い精度を保証できない問題の一つとしては、経験的なパラメータとその関数が固定という問題点である。これに対しNNPは以下の利点がある（引用[1]

Energies can be fitted to high accuracy with very small remaining errors compared to the underlying reference data.
基礎となるデータと比較して、非常に小さな残差誤差で高精度に適合できます。
NNPs can be calculated efficiently and require much less CPU time than electronic structure calculations.
NNPは効率的に計算することができ、DFTによりもはるかに少ないCPU時間ですむ。
No knowledge about the functional form of the PES is required.
エネルギー曲面についての知識は不要
The NN energy expression is unbiased, generally applicable to all types of bonding and does not require system‐specific modifications.
一般にすべてのタイプの結合に適用可能であり、システム固有の変更を必要としません。

　以上まとめると
（古典力場と比べて）高い精度と自由度で、（DFTと比べて）高速に計算するポテンシャルを開発することが目的となっている。

HDNNPの構造

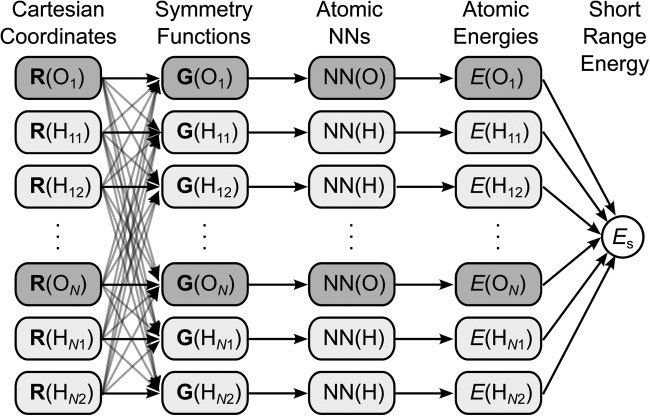
　HDNNPの概要図を図１に示す。Rとは、それぞれの原子の座標を示す。GはSymmetry Functionとよばれ、対象の原子とその周辺の原子の距離や角度に基づく関数を用いて計算される（(1)(2)式参照）。(2)式にあるように、Gは多次変数となっており、これをNeural Network（=MultiLayer Perceptron:MLP）に導入して、各原子寄与エネルギーを計算して、最後のその合計を計算して系のエネルギーとする。

図１ HDNNPの概要図^[1]　

カットオフ関数

\begin{align}
f_{c,1}(R_{ij}) \Biggl\{{
\begin{array}{ll}
0.5 \cdot [\cos (\pi R_{ij}/R_c)+1] & for & (R_{ij} \leq R_c) \\
0.0 & for & (R_{ij} > R_c)
\end{array} \tag{1}}
\end{align}

Symmetry Function

\begin{align}
\textbf{G}_i &= [
\begin{array}{llll}
G_{i,0} & G_{i,1} & \cdots G_{i,n}
\end{array}
]\tag{2} \\
G^2_i &= \sum^{N_{atom}}_{j=1}e^{- \eta (R_{ij}-R_s)^2} \cdot f_c(R_{ij}) \tag{2.1}\\
G^3_i &= 2^{1-\zeta} \sum_{j \neq i}\sum_{k \neq i,j}[(1+\lambda\cdot \cos \theta_{ijk})^\zeta\cdot e^{- \eta (R_{ij}+R_{ik}+R_{jk})^2}\cdot f_c(R_{ij})\cdot f_c(R_{ik}) \cdot f_c(R_{jk})]\tag{2.2}
\end{align}

力

　分子動力学計算を行うときは、各原子に作用する力を計算して運動方程式を積分する。

m\frac{\partial^2x}{\partial t^2}=F_\alpha=F_{\alpha,s}+F_{\alpha,elec}=-\frac{\partial E_s}{\partial x}-\frac{\partial E_{elec}}{\partial x} \tag{3}

　このように、エネルギーの計算が可能になると系の時間発展の予測が可能となり、非常に有用である。
　ここで、HDNNPの力の計算について説明する。対称性関数はすべて微分可能な関数によって構築されており、$\frac{\partial G}{\partial R}$が計算可能である。またMLPは当然ながら微分可能である$\frac{\partial E}{\partial G}$。つまり、これらの積を求めることで、
$$
\frac{\partial E_s}{\partial x}=\frac{\partial E_s}{\partial R}=\frac{\partial E}{\partial G}\frac{\partial G}{\partial R} \tag{4}
$$
　のように力が計算可能である。

Graph Convolution Neural Network: GCNN^[2,3,5] / Message Passing Neural Network: MPNN^[6]

reference 補足

　Graph Convolutionという名前は、画像分野でCNNが登場してから生まれた名前であり、このGCNNとして初めてConvolutionという銘打ったのはおそらく[2]の論文である。
　ただし、Convolutionという方法に対してSpectral Methods派とNon-Spectral Methods派で大きく分かれていた（？：いまいちよく違いが分かってない）。この[2]、[3]の方法はSpectral Methodsを用いた方法であるが、現在主流なGCNはより計算が容易なNon-Spectral Methodsである。今の定義におけるGCNの最初期のモデルは[5]と考えられる（ちがったら教えてください）。この議論については、[4,6]を参照されたい。

GCNNとMPNNについて

　コンピュータビジョン分野(CV)において、Convolution layerを持つDeep Learningが活躍しこの理論を様々なデータの形に応用しようという研究が行われている。
　Convolutionはデータの構造がユークリッド空間上で定義されている。分子構造やソーシャルネットなどのノードとエッジで表現されるグラフ構造では定義されていない。GCNNは局所構造の畳み込みという考えをグラフという構造に適応させた手法である。
GCNに関する多くのモデルが提案されるなか、Gilmerらは、GCNsの多くの共通構造を見出し、これをMessage Passing Neural Networkと呼ばれる構造を提案した。

Message Passing Neural Network

MPNNsの基本構造を下記に示す。各ノードの特徴項は$h_i$、エッジは$e_{ij}$、$N(i)$は$i$ノードの周辺（接合）ノード集合を示す。

\begin{align}
m^{t+1}_\nu&=\sum_{w\in N(\nu)}M_t(h^t_\nu,h^t_w,e_{\nu w}) \tag{5} \\
h^{t+1}_\nu&=U_t(h^t_\nu,m^{t+1}_\nu) \tag{6} \\
\hat{y}&=R(\{h^T_\nu | \nu \in G\}) \tag{7} \\
\end{align}

ここで、$M_t$はmessage関数、$U_T$はupdate関数、$R$はreadout関数と呼ばれている。GCNの種類によってこの三つの関数は様々であるが、すべてこの三つの関数によって表現できるというのがMPNNの考えである。[5]で表にまとめられているので、そちらを参照されたい。$R$は出力層である。

本題

　HDNNPの構造は、ある原子の座標から、カットオフ圏内の原子についてその距離をsymmetry functionによって収集している構造となっている。これはMPNNでいうところのMessage functionと同一であると見れる。
　また、周辺原子の情報を集約したうえで、MLPを通してエネルギーを取得する。これは、update function と同一と見れる。
　以下、HDNNPをMPNNとして書き換えた例を示す。

\begin{align}
M_t(r_\nu,r_w,e_{\nu w})&=\textbf G = \Biggl\{{
\begin{array}{ll}
G^2_i &= \sum^{N_{atom}}_{j=1}e^{- \eta (R_{ij}-R_s)^2} \cdot f_c(R_{ij}) \\
G^3_i &= 2^{1-\zeta} \sum_{j \neq i}\sum_{k \neq i,j}[(1+\lambda\cdot \cos \theta_{ijk})^\zeta\cdot e^{- \eta (R_{ij}+R_{ik}+R_{jk})^2}\cdot f_c(R_{ij})\cdot f_c(R_{ik}) \cdot f_c(R_{jk})]
\end{array} \tag{8}
} \\
U_t(h^t_\nu,m^{t+1}_\nu)&=MLP(h^t_\nu) \tag{9} \\
R(h^T_\nu)&=\sum_{\nu \in G}h^T_\nu \tag{10}
\end{align}

reference

[1] Jörg Behler, Constructing high‐dimensional neural network potentials: A tutorial review,Inter. J. Quant. Chem., 12, (2015)
[2] Michaël Defferrard, Xavier Bresson, Pierre Vandergheynst, Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering, NIPS 2016
[3] Thomas N. Kipf, Max Welling, Semi-Supervised Classification with Graph Convolutional Networks, arXiv:1609.02907
[4] Jie Zhou, Ganqu Cui, Zhengyan Zhang, Cheng Yang, Zhiyuan Liu, MAosong Sun, Graph Neural Networks: A Review of Methods and Applications, arXiv:1812.08434
[5] F. Scarselli, M. Gori, A. Chung Tsoi, M. Hagenbuchner, G. Monfardini, The graph neural network model, IEEE Transactions on Neural Networks, 20 (2009)
[6] Justin Gilmer, Samuel S. Schoenholz, Patrick F. Riley, Oriol Vinyals, George E. Dahl, Neural Message Passing for Wuantum Chemistry, arXiv:1704.01212

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up