はじめに
本記事は、大学~大学院程度の知識を有する確率統計に興味のある人向けにベイズ推論を解説する記事です。
2020年センター試験の数学1・Aに登場したロボットの問題が難しかったので記事にしました。
私は条件付き確率を高校で習わなかった気がするので、最近の高校生は難しいことをやっているんだなあと関心しました。
実は、この設問に正答を与えるだけなら非常に簡単です。
おそらくこのロボット問題自体も、頭の柔らかい高校生でしたら簡単でしょう。
第3問 [1]
この設問ですが、解答を与えるだけなら非常に簡単です。
上から解いていけば0と2が正しいとわかるので、3のロボット問題は自動的に誤りとなります。
私も試験中なら、この問題を読むことすらしないでしょう。
問題文は以下の通りです。
③ コインの面を見て「オモテ(表)」または「ウラ(裏)」とだけ発言するロボットが2体ある。ただし、どちらのロボットも出た面に対して正しく発言する確率が0.9、正しく発言しない確率が0.1であり、これら2体は互いに影響されることなく発言するものとする。いま、ある人が1枚のコインを投げる。出た面を見た2体が、ともに「オモテ」と発言したときに、実際に表が出ている確率を$p$とすると、$p\leq0.9$である。
高校生的な解答
まず、高校生が使える数学を用いて解いてみます。
といっても、高校生の参考サイトを見て書いてある内容だけで解いたって感じで、実際の授業でどう教えているかは知らないのですが。。。
(数学的な誤解を恐れず、直感的な日本語で書けば)条件付き確率は、
\frac{事象と条件が同時に生起する確率}{条件が生起する確率}
で与えられます。数学チックにいえば、
\frac{P(A \cap B)}{P(B)}
となります。今はAがコインが実際に表となる事象であり、Bがロボット2体が同時に表と発言する事象であるので、
\begin{align}
& \frac{P(A \cap B)}{P(B)} \\
=& \frac{P(コインが実際に表となる) \cap (ロボット2体が同時に表と発言する)}{P(ロボット2体が同時に表と発言する)} \\
=& \frac{0.5*0.9*0.9}{0.5*0.1*0.1+0.5*0.9*0.9} \\
=& 0.9878\cdots
\end{align}
となりこの問題は「偽」である、が答えです。
分母が難しいですが、ロボット2体が同時に表と発言する確率は、コインがオモテであるケースと、ウラであるケースを足し合わせれば、コインに依存しないロボット2体の確率が出せる、という解釈です。
このあたり、周辺化を知らない高校生は分母の理解に苦しむのではないでしょうか?
「他の設問を解いてこの問題に回答してね」という出題者の意図が感じられます。
より厳密に解く
ここからの話は大学以降の範囲になります。
問題定義とモデル化
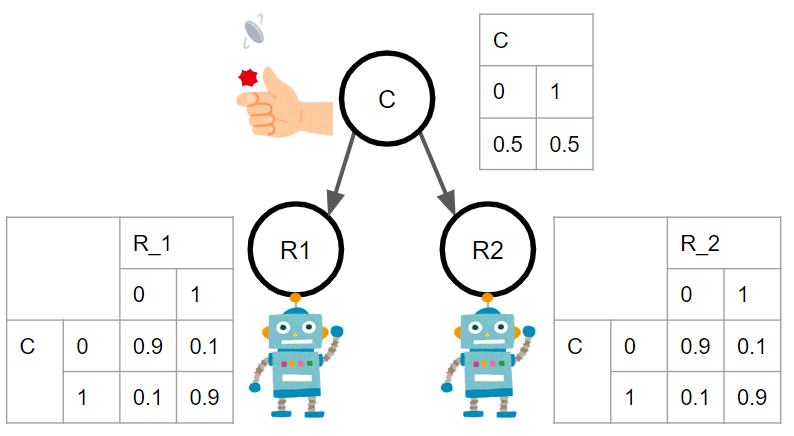
問題をグラフィカルモデルで表現し、条件付き確率表(CPT)を示します。
コインの裏表の確率変数を$C$として、裏を$C=0$、表を$C=1$とすると、
P(C=0) = 0.5 \\
P(C=1) = 0.5
と表せます。n体目のロボットの発言の確率変数を$R_n$として、裏を$R_n=0$、表を$R_n=1$とすると、
P(R_n=0|C=0) = 0.9\\
P(R_n=1|C=0) = 0.1\\
P(R_n=0|C=1) = 0.1\\
P(R_n=1|C=1) = 0.9
と表せます。加えて、ロボットは互いに影響されることなく発言するので、コインの面が与えられた条件下で独立(条件付き独立)であり、
P(R_1, R_2|C) = P(R_1|C)P(R_2|C)
が成り立ちます。
ここまでが設問で与えられた前提条件です。ごく単純なベイジアンネットワークの例題と言えるでしょう。
ここで、$P(R_n=1)$は周辺化によって
\begin{align}
& P(R_n=1) \\
=& P(R_n=1|C=0)P(C=0) + P(R_n=1|C=1)P(C=1) \quad (周辺化)\\
=& 0.1\cdot0.5 +0.9\cdot0.5 \\
=& 0.5
\end{align}
と簡単に求まります。
解くだけなら簡単
求めるべきは$P(C=1|R_1=1, R_2=1)$です。
ベイズの定理や周辺化を駆使すれば簡単に既知の変数のみで表すことができます。
\begin{align}
& P(C=1|R_1=1, R_2=1) \\
=& \frac{P(C=1, R_1=1, R_2=1)}{P(R_1=1, R_2=1)} \quad (ベイズの定理)\\
=& \frac{P(R_1=1, R_2=1|C=1)P(C=1)}{P(R_1=1, R_2=1)} \\
=& \frac{P(R_1=1|C=1)P(R_2=1|C=1)P(C=1)}{P(R_1=1, R_2=1)} \quad (条件付き独立を利用) \\
=& \frac{P(R_1=1|C=1)P(R_2=1|C=1)P(C=1)}{P(R_1=1, R_2=1|C=0)(C=0) + P(R_1=1, R_2=1|C=1)(C=1)} \quad (周辺化) \\
=& \frac{0.5\cdot0.9\cdot0.9}{0.5\cdot0.1\cdot0.1+0.5\cdot0.9\cdot0.9} \\
=& 0.9878\cdots
\end{align}
高校生的な解答は、これを日本語で表現したにすぎません。
むしろ、高校生的な解答は言語的な誤解が含まれる恐れがあるため、このように厳密に考えることが理想でしょう。
ロボットのパラドクス
さて、ここからが本題です。解いていて、少し面白いなと感じた話を共有します。
このロボットたちは互いに何の影響も及ぼしません。ロボット2がなんと言おうと、ロボット1の発言が変わることがないはずです。
しかし、ある状況下で、ロボットたちは互いに影響を及ぼすように見えます。
モンティ・ホール問題のように、人間の直感的感覚と実際の理論的解答が乖離するのです。
ロボットの独立性
章「解くだけなら簡単」で紹介した数式の分母の展開に違和感を感じませんか?
ロボットたちは互いに影響を及ぼさないのだから、
\begin{align}
P(R_1=1, R_2=1) = P(R_1=1)P(R_2=1)
\end{align}
が成り立ちそうで、これを使えば簡単に計算できるのでは?
しかし、この式変形は間違っています。$P(R_1=1, R_2=1) \neq P(R_1=1)P(R_2=1)$です。
ロボット同士は「条件付き独立」です。コインCが明らかになった条件化でのみ、$P(R_1, R_2|C) = P(R_1|C)P(R_2|C)$が成り立ちます。
正しい$P(R_1=1, R_2=1)$の展開は、
\begin{align}
&P(R_1=1, R_2=1) \\
=& P(R_1=1|R_2=1)P(R_2=1) \\
\end{align}
であり、$P(R_1=1|R_2=1)$は、
\begin{align}
& P(R_1=1|R_2=1) \\
=& P(R_1=1|R_2=1, C=0)P(C=0|R_2=1) + P(R_1=1|R_2=1, C=1)P(C=1|R_2=1) \\
=& P(R_1=1|C=0)P(C=0|R_2=1) + P(R_1=1|C=1)P(C=1|R_2=1) \\
=& 0.1\cdot0.1 +0.9\cdot0.9 \\
=& 0.82
\end{align}
と計算できます。
これはギョッとする結果です。$P(R_1)=0.5$ですので、ロボット2が「オモテ」と発言した段階で、ロボット1が「オモテ」と発言する確率が0.5から0.82に増加してしまったのです。
ロボット2の発言に伴い、ロボット1の発言が変わってしまったように感じます。
ロボット1とロボット2は互いに無関係のはずなのに、不思議に感じます。
なぜ、ロボット1の発言はロボット2に依存してしまうのか
このパラドクスは、コインが見えていないことによって生じています。
先ほども説明したように、コインが見えている条件下では、ロボットの発言は条件付独立となり、互いに影響を及ぼしません。
しかし、コインが見えていない状況で、ロボット2が発言するとどうなるでしょうか?
ロボット2がオモテと発言した場合、コインがオモテである確率が上昇してしまうのです。
実際$P(C=1|R_2=1)$は、ベイズの定理より
\begin{align}
& P(C=1|R_2=1) \\
=& \frac{P(R_2=1|C=1)P(C=1)}{P(R_2=1)} \\
=& \frac{0.9\cdot0.5}{0.5} \\
=& 0.9
\end{align}
となります。
ロボット2がオモテと言うと、コインがオモテである確率が0.5から0.9に上昇します。
これより、ロボット2がオモテというと、コインがオモテである確率が上昇し、ひいてはロボット1がオモテと言う確率が上がる、ということになります。
まだ直感的に理解できない?
そしたら、ロボットの数を増やして考えてみます。
N体のロボットを考えると、人間の直感にも近くなっていきます。
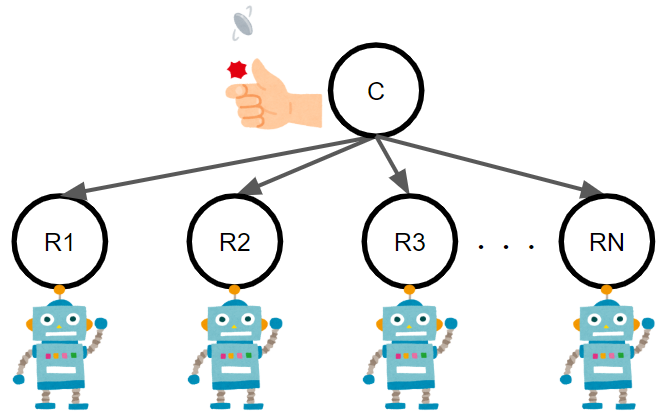
N体のロボットを考える。
ロボットがN体存在し、それぞれが別々にコインのウラオモテを判定する場合を考えます。
ロボットがコインの出目に対する条件付き独立ですので、
P(R_1, R_2, \dots, R_N|C) = \prod_{i=1}^N P(R_i|C)
が成り立ちます。
N体のすべてのロボットがオモテと発言した時、コインが実際にオモテである確率は、2体の時と同様の計算で、
\begin{align}
& P(C=1|R_1=1, R_2=1, \dots, R_N=1) \\
= & \frac{P(C=1)\prod_{i=1}^N P(R_i=1|C=1)}{P(R_1=1, R_2=1, \dots, R_N=1)} \\
= & \frac{P(C=1)\prod_{i=1}^N P(R_i=1|C=1)}{P(R_1=1, R_2=1, \dots, R_N=1 | C=0)P(C=0) + P(R_1=1, R_2=1, \dots, R_N=1 | C=1)P(C=1)} \\
= & \frac{P(C=1)\prod_{i=1}^N P(R_i=1|C=1)}{P(C=0)\prod_{i=1}^N P(R_i=1|C=0) + P(C=1)\prod_{i=1}^N P(R_i=1|C=1)} \\
= & \frac{0.5\cdot0.9^N}{0.5\cdot0.1^N + 0.5\cdot0.9^N} \\
= & \frac{0.9^N}{0.1^N + 0.9^N}
\end{align}
となります。とても綺麗な式になりました。
実際、$N=2$を代入すると、2体のロボットの解答と一致します。
この式は$N\rightarrow\infty$の極限で1となります。ロボットが無限体存在し、全てがオモテと発言すれば、コインを見ずともオモテとわかります。
次に、ロボット2〜Nがオモテと発言した時に、ロボット1がオモテと発言する確率$P(R_1=1|R_2=1, R_2=1, \dots, R_N=1)$は、
\begin{align}
& P(R_1=1|R_2=1, R_3=1, \dots, R_N=1) \\
=& P(R_1=1|C=0)P(C=0|R_2=1, R_3=1, \dots, R_N=1) \\
&+ P(R_1=1|C=1)P(C=1|R_2=1, R_3=1, \dots, R_N=1) \\
=& P(R_1=1|C=0) \frac{0.1^{N-1}}{0.1^{N-1} + 0.9^{N-1}} + P(R_0=1|C=1) \frac{0.9^{N-1}}{0.1^{N-1} + 0.9^{N-1}} \\
=& \frac{0.1^N}{0.1^{N-1} + 0.9^{N-1}} + \frac{0.9^N}{0.1^{N-1} + 0.9^{N-1}} \\
=& \frac{0.1^N + 0.9^N}{0.1^{N-1} + 0.9^{N-1}} \\
\end{align}
となります。これも綺麗な式ですね。
これも$N=2$の代入で2台ロボットのケースと確かに一致します。
この式は$N\rightarrow\infty$の極限で0.9となります。ロボットが無限体存在し全てがオモテと発言すれば、コインを見ずともオモテとなるので、ロボット1のオモテと発言する確率0.9が現れる結果は妥当と言えます。
ロボットの台数を変化させた場合の結果は以下の通りです。
\begin{align}
&P(R_1=1) &=& 0.5 \\
&P(R_1=1|R_2=1) &=& 0.820 \\
&P(R_1=1|R_2=1, R_3=1) &=& 0.890 \\
&P(R_1=1|R_2=1, R_3=1, R_4=1) &=& 0.899 \\
\end{align}
これならば、「コインは見えていないが、他の大勢のロボットがオモテというのだから、コインはオモテなのだろう。だから、ロボット1がオモテという確率は0.5より高いはずだ」と、直感的に理解できるのではないでしょうか。
ロボット2体の場合に違和感を感じる理由は、ロボット2体が対等の関係だと脳が勝手に考えてしまうからかもしれませんね。
ロボット2の発言にロボット1が影響されるわけないだろうと考える一方で、大勢のロボットの発言はロボット1に影響を及ぼしそうだとは考えられるのでしょう。
多数決を重んじる動物のサガなのかもしれません。
なぜ、ロボット2体の時に直感と反するかという問題は、モンティ・ホール問題にも通じるところがあります。
モンティ・ホール問題を直感的に理解できない人でも、扉を100個にしたモンティ・ホール問題はすんなり理解できます。
グラフィカルモデル
ここまで行ってきた議論は、当然私が初めて考えたわけではありません。
グラフィカルモデルや、ベイジアンネットワークと呼ばれる分野の特殊なケースにすぎません。
具体的には、本ロボット問題はtail-to-tailのグラフ推論の例と言えるでしょう。
疲れたのでこれ以上解説はしません。。。気になった人はグラフィカルモデルでググってください。
モンテカルロ・シミュレーション
これまでの議論が正しいかどうかを確かめるために、モンテカルロ・シミュレーションを行います。
pythonでコインを10万回投げました。
モンテカルロ・シミュレーションのソースコード(長いのでたたんでいます。)
# -*- coding: utf-8 -*-
# %%
import numpy as np
import pandas as pd
# %%
N = 100000
robot_num = 2
result = []
# %%
coin = np.zeros((N, 1), dtype = int)
robot = np.zeros((N, robot_num), dtype = int)
for i in range(N):
coin[i] = np.random.randint(0, 2)
robot_rand = np.random.random(robot_num)
for n_robot, tmp in enumerate(robot_rand):
if tmp <= 0.9 :
robot[i, n_robot] = coin[i]
else :
robot[i, n_robot] = coin[i] ^ 1
# %%
result = pd.DataFrame(np.concatenate([coin, robot], axis = 1), columns = ["coin", "robot1", "robot2"])
all_1 = result[(result.robot1 == 1) & (result.robot2 == 1)]
p = (all_1.coin == 1).sum()/all_1.shape[0]
# %%
p_truth = (0.5*0.9*0.9)/(0.5*0.9*0.9+0.1*0.1*0.5)
print("ロボット2体がオモテと発言したときのコインの条件付き確率(理論):{}".format(p_truth))
print("ロボット2体がオモテと発言したときのコインの条件付き確率(実験):{}".format(p))
# %%
r12 = result[result.robot2 == 1]
p12 = (r12.robot1 == 1).sum() / r12.shape[0]
p12_truth = 0.9*0.9+0.1*0.1
print("ロボット2がオモテと発言した時のロボット1の条件付き確率(理論):{}".format(p12_truth))
print("ロボット2がオモテと発言した時のロボット1の条件付き確率(実験):{}".format(p12))
プログラムの出力結果は下記です。
10万回ではまだまだ誤差がありますが、だいたい一致していることが確認できます。
ロボット2体がオモテと発言したときのコインの条件付き確率(理論):0.9878048780487805
ロボット2体がオモテと発言したときのコインの条件付き確率(実験):0.988986730708585
ロボット2がオモテと発言した時のロボット1の条件付き確率(理論):0.8200000000000001
ロボット2がオモテと発言した時のロボット1の条件付き確率(実験):0.8214371114299378
以下、雑多なこと
最後に、思いついたことをつらつら書いていきます。
M面体サイコロ
コイン、すなわちベルヌーイ分布を取り扱う問題でしたが、M面体サイコロのようなものを考えることで、カテゴリカル分布の場合でも同様の議論ができます。
ある面$m^\prime$が出る確率を $P(C=m^\prime|R_1=r_1, R_2=r_2, \dots, R_N=r_N)$とすると、
\begin{align}
& P(C=m^\prime|R_1=r_1, R_2=r_2, \dots, R_N=r_N) \\
= & \frac{P(C=m^\prime)\prod_{i=1}^N P(R_i=r_i|C=m^\prime)}{P(R_1=r_1, R_2=r_2, \dots, R_N=r_N)} \\
= & \frac{P(C=m^\prime)\prod_{i=1}^N P(R_i=r_i|C=m^\prime)}{\sum_{m=1}^M P(R_1=r_1, R_2=r_2, \dots, R_N=r_N | C=m)P(C=m)} \\
= & \frac{P(C=m^\prime)\prod_{i=1}^N P(R_i=r_i|C=m^\prime)}{\sum_{m=1}^M P(C=m)\prod_{i=1}^N P(R_i=r_i|C=m)}
\end{align}
となります。
ベイズ推論的考察
ロボットの追加をデータ点の追加と考えれば、よくあるベイズ推論モデルと全く同一の議論ができることがわかります。
ガウス分布のノイズが乗ったデータ点で回帰モデルのパラメータを推定することと、気まぐれなロボットからコインの裏表を推定することは同じ計算を行います。
\begin{align}
& P(C=m^\prime|R_1=r_1, R_2=r_2, \dots, R_{N+1}=r_{N+1}) \\
\propto & P(C=m^\prime) \prod_{i=1}^{N+1} P(R_i=r_i|C=m^\prime) \\
= & P(C=m^\prime) \prod_{i=1}^N P(R_i=r_i|C=m^\prime)) \times P(R_{N+1}=r_{N+1}|C=m^\prime) \\
\propto & P(C=m^\prime|R_1=r_1, R_2=r_2, \dots, R_N=r_N) \times P(R_{N+1}=r_{N+1}|C=m^\prime)
\end{align}
と書けます。
$P(C=m^\prime|R_1=r_1, R_2=r_2, \dots, R_N=r_N)$が計算できていれば、追加ロボット${N+1}$の確率を掛けるだけで、すべてを再計算することなく全体の確率を計算できることを意味します。
データ点を追加してパラメータを推論するときの議論と同じですね。
最後に
受験生がんばってください。
やりのこしたこと
以下、意欲が湧けば記事にします。
-
コインが2枚、ロボットが1体の場合
head-to-headのモデルの議論です。
今回の問題よりもっと難しくなります。 -
コインの裏表の出る確率、ロボットの発言の確率が未知の場合
MCMCで確率推定する方法です。
解説はとても大変なので、やる気がでなさそう。