本記事の目的
大好きな海外ドラマ(とあるシチュエーションコメディ)を見ていて気になったことがありました。
登場人物の物理学者(博士)は、友人の発言がきっかけで研究資金調達のためラスベガスへ行った際にこんな事を言ってました。
「(吹替)何時間もこのルーレットを観察してカイ二乗検定をしたんだ!それでボールが落ちやすいポケットがどれなのかわかった!32,17,5だ!このルーレット盤交換しないでくれる?大きく賭けたい!!」
この後、カジノスタッフに連行されてしまう博士ですが・・・。
ここでは博士が行ったカイ二乗検定について想像しながら見ていきたいと思います。
ルーレットのデータ
博士は何時間もこのルーレットを観察して・・・と言っているので、ここでは3時間と仮定、ルーレット1ゲームを1分と仮定すると、180個のデータを観測したとします。
ルーレットで観測できるデータは以下の画像で見ていきます。当たり障りのないところでWikipedia様からの引用です。
ルーレット回転盤

ルーレットテーブル
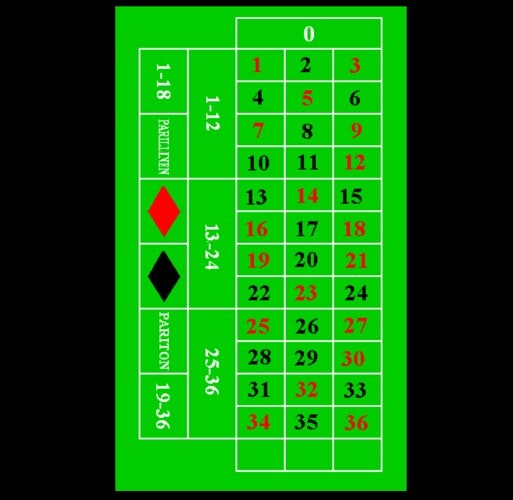
(画像出典:https://ja.wikipedia.org/wiki/%E3%83%AB%E3%83%BC%E3%83%AC%E3%83%83%E3%83%88)
ディーラーは1個のボールをルーレット回転盤に投げ入れるので、1ゲームで得られるデータは1個になります。
また、赤黒に数字が分かれてますが、数字の重複はないため、0~36までのいずれかにボールが落ちるということになります。ここではサンプル的に以下のデータを使用していきます。
| ポケット(ルーレット盤の数字) | 出現回数(観測度数) |
|---|---|
| 0 | 2 |
| 1 | 6 |
| 2 | 5 |
| 3 | 4 |
| 4 | 2 |
| 5 | 11 |
| 6 | 5 |
| 7 | 2 |
| 8 | 5 |
| 9 | 4 |
| 10 | 6 |
| 11 | 2 |
| 12 | 6 |
| 13 | 4 |
| 14 | 8 |
| 15 | 7 |
| 16 | 2 |
| 17 | 12 |
| 18 | 3 |
| 19 | 4 |
| 20 | 5 |
| 21 | 6 |
| 22 | 3 |
| 23 | 7 |
| 24 | 3 |
| 25 | 8 |
| 26 | 1 |
| 27 | 5 |
| 28 | 1 |
| 29 | 6 |
| 30 | 4 |
| 31 | 2 |
| 32 | 11 |
| 33 | 7 |
| 34 | 5 |
| 35 | 4 |
| 36 | 2 |
適合度検定
ルーレットデータを見ると5、17、32の出現回数が他より多いことがわかりますが(意図的に増やしてます。)、これが統計的に理論値と差があるのか、ないのかわかりません。
カイ二乗検定をよく使うケースとして、2×複数のクロス表の2変数(行列)が独立か、独立でないかを検定する「独立性の検定」と、観測度数分布が理論上の期待度数分布(理論値)とどれだけ一致しているかを検定する「適合度検定」があります。
今回は、後者の適合度検定を使用し、全てのポケットには等しい確率でボールが入るとして180/37※を期待度数とする理論値と観測値の分布が一致しているかを検定していきます。
※180はデータ総数、37は全ポケット数
帰無仮説と対立仮説
帰無仮説・・・観測した分布は理論値の分布と一致する(度数分布に偏りがない)
対立仮説・・・観測した分布は理論値の分布と一致しない(度数分布に偏りがある)
適合度検定の実施
計算方法は多くの記事や書籍で記載されていますし、ExcelでもPythonでも簡単に算出できますので省略します。
(観測度数ー期待度数)²)/期待度数 を計算し、その総和(検定統計量Χ²)を求めますが、今回の期待度数iはiによらず全て同じ値(=180/37)です。
\chi^2=\sum \frac{(観測度数i-期待度数i)^2}{期待度数i}
結果(カイ二乗値とp値)
Pythonで計算した結果を以下に示します。有意水準は5%とします。
from scipy import stats
observed_freq = [2, 6, 5, 4, 2, 11, 5, 2, 5, 4, 6, 2, 6, 4, 8, 7, 2, 12, 3, 4, 5, 6, 3, 7, 3, 8, 1, 5, 1, 6, 4, 2, 11, 7, 5, 4, 2]
expected_freq = []
for i in range(0,37):
expected_freq.append(180/37)
result = stats.chisquare(observed_freq, expected_freq)
print('カイ二乗値:{0} p値:{1}'.format(round(result.statistic,3),round(result.pvalue,3)))
カイ二乗値:55.156 p値:0.021
p値<0.05のため、帰無仮説を棄却し、検定結果は対立仮説を採択「観測した分布は理論値の分布と一致しない(度数分布に偏りがある)」となります。
考察
博士は、上記のような検定を行ったのかなと想像します。
ルーレットを観察し収集したデータは、理論データ(全てのポケットに等しくボールは入り、偏りがないデータ)と比較して、偏りがある、と判断し、観測データの分布から5、17、32の相対度数が他より高いので、ボールが落ちやすいポケットであると判断したのではないでしょうか。
ポケットだけでなく、赤黒の色でも偏りを見ているかもしれません。
あくまでドラマの話ですし想像でしかないですが、同じように考えてみたことのある人は教えてください!