【機械学習】主成分分析を理解する

本記事の目的

• 主成分分析の用語や算出する指標を理解する
• 主成分を使用した回帰モデルを構築し、その解釈性や主成分を使用しないパターンとの精度を比較してみる

主成分分析とは

• 目的は「大量の変数をなるべく少ない変数にデータの情報量を保ちながら縮小させること」である
• 主成分分析自体が目的になることはほとんどなく、元のデータの情報量を残しつつわかりやすいデータに変換するための手法の1つとして、前処理段階で行われる
• 主成分分析の算出過程の根本は、共分散行列から「固有値」と、固有値に対応する「固有ベクトル」を求めることであり、［求めた固有値＝主成分得点の分散］、［固有値に対応する固有ベクトル＝主成分負荷量］の関係である
• 「データの分散が最もi番目に大きなところを通る軸を求めること」と「共分散行列におけるi番目に大きな固有値と対応する固有ベクトルを求めること」は同義であり、「分散が大きなところを通す」ということは元データの損失が少ないことを意味する
  （以下、2変数を参考に）

用語解説

用語	解説
固有値	各主成分が持つ情報量（＝主成分得点の分散）と同義であり、固有値が大きいものから順に第〇主成分が割り振られる。変数の数だけ存在する（投入した変数が10個であれば10個の主成分が存在）
固有ベクトル	1つの固有値に対し変数の数だけ算出される（投入した変数が10個であれば1つの固有値に対し10個存在）。主成分負荷量と同義
主成分負荷量	第〇主成分負荷量は、第〇番目の固有値に対応する固有ベクトルと同義であり、その主成分に対し、各変数がどれだけ寄与しているかを示す。主成分負荷量がプラスの場合、その変数と主成分は正の関係にあり、マイナスの場合、負の関係であることを示す。符号を除いた値が大きいほど、その変数は主成分の形成に大きく寄与している
主成分得点	主成分負荷量により元のデータを変換したもの
寄与率	各主成分の固有値を固有値全体の割合に変換したもの。一般的に第〇主成分までの累積寄与率を算出し、70%~80%を超える点までの主成分を選択すると良いとされている

ミニマムのデータで見る

以降で使用するライブラリ

import pandas as pd
import numpy as np
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import warnings
warnings.simplefilter("ignore")
import seaborn as sns
from statsmodels.miscmodels.ordinal_model import OrderedModel
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA

擬似的に作成した「5人分の学校のテスト結果」を使用する。理系科目内、文系科目内それぞれで強い相関が出るように作成している

全科目を得意とする：1人
全科目が不得意：1人
全科目で並：1人
文系のみ得意・やや得意とする：2人

# ミニマムデータの作成
data = pd.DataFrame({'数学':[89,10,45,20,30],
                     '化学':[80,15,67,22,30],
                     '国語':[75,65,60,10,80],
                     '英語':[85,70,55,18,88]})

# 相関行列の作成入れる
plt.figure(figsize=(5, 3))
sns.heatmap(data.corr(),annot=True, fmt='.2f',cmap='GnBu')
```python
<img width="300" alt="image.png" src="https://qiita-image-store.s3.ap-northeast-1.amazonaws.com/0/2642161/dda7a706-35fc-6cb7-172f-6e2e84a0a980.png">

## 固有値・固有ベクトルを計算
4科目、つまり変数が4つ存在するため、固有値も4つ存在する。
```python
# 共分散行列を算出
cov = data.cov()

# 固有値と固有ベクトルを算出
eig_val, eig_vec = np.linalg.eig(cov)

print('第1主成分の固有値：{}'.format(eig_val[0]))
print('第2主成分の固有値：{}'.format(eig_val[1]))
print('第3主成分の固有値：{}'.format(eig_val[2]))
print('第4主成分の固有値：{}'.format(eig_val[3]))

第1主成分の固有値：2296.8055737462914
第2主成分の固有値：1009.2802161930731
第3主成分の固有値：77.43112879664118
第4主成分の固有値：0.08308126399184189

第1~2主成分の固有値が大きいため、以降はここに絞って見ていく

固有ベクトル（主成分負荷量）の可視化

print('第1主成分の固有ベクトル：{}'.format(eig_vec[:, 0]))
print('第2主成分の固有ベクトル：{}'.format(eig_vec[:, 1]))

第1主成分の固有ベクトル：[0.55749999 0.49735548 0.46803137 0.47199356]
第2主成分の固有ベクトル：[ 0.4581633 0.48329547 -0.51619498 -0.53856718]

各科目の第1~2主成分負荷量を可視化し、主成分を解釈してみる

# 固有ベクトルをデータフレームに入れる
eigen_vector = pd.DataFrame(eig_vec,columns=['component_1','component_2','component_3','component_4'],index=data.columns)

# プロット
plt.figure(figsize=(5, 3))
for x, y, name in zip(eigen_vector['component_1'], eigen_vector['component_2'], eigen_vector.index):
    plt.text(x, y, name)
plt.scatter(eigen_vector['component_1'], eigen_vector['component_2'], alpha=0.8)
plt.plot([0.45,0.6], [0,0],linestyle='--',color='black')
plt.plot([0,0],[-0.6,0.6],linestyle='--',color='black')
plt.grid()
plt.xlabel('component_1')
plt.ylabel('component_2')
plt.xlim(0.45,0.6)
plt.ylim(-0.6,0.6)
plt.show()

• 第1主成分：変数全てで正の関係であるため、「総合的な学力」のような主成分ぽい
• 第2主成分：数学と化学で正の関係、国語と英語で負の関係であり、その大きさは同程度。「文理特化力」のような主成分ぽい

主成分得点の計算と可視化

5人の第1~2の主成分得点をプロットする

# 中心化（=データ - 平均値）
data_tmp = data.copy()
for col in data_tmp.columns:
    data_tmp[col] = data_tmp[col] - data_tmp[col].mean()

# 主成分得点を算出
result = pd.DataFrame()
for com in eigen_vector.columns:
    result = pd.concat([result,pd.DataFrame(np.dot(data_tmp, eigen_vector[com]),columns=[com])],axis=1)

# 可視化
plt.figure(figsize=(5,3))
plt.scatter(result['component_1'],result['component_2'],label='主成分得点')
plt.plot([result['component_1'].min(),result['component_1'].max()], [0,0],linestyle='--',color='black')
plt.plot([0,0],[result['component_2'].min(),result['component_2'].max()],linestyle='--',color='black')
plt.grid()
plt.xlabel('第1主成分')
plt.ylabel('第2主成分')
plt.legend(loc='upper right')
plt.show()

• 第1主成分の総合力では突出して高い・低い2人が存在する
• 第2主成分の文理特化力では2人が負の値になっている

従って、4変数（4科目）を次元削除し、2主成分にしても元データの特徴を表せていることがわかる

上記まではライブラリ「PCA」を使用せずに実装してきた。以降はデータ量を増やし「PCA」を使用するパターンで見ていく

主成分分析を使用したモデル構築

課題設定

本校では2年生の期末テスト成績を元に翌3年生初頭から始まる特講クラスの振り分けを行っている。
近年は大学受験に向けたカリキュラムの変更に伴い、学校側で特講クラスの事前準備が嵩み、教員の残業等の負担が増加している。早めに大体の特講クラスの振り分け人数を把握できれば、事前準備期間を長めに取れるため、負担減に繋がりそう。
過去数年分の中間テスト結果と期末成績から期末成績を予測できないか。

上記の課題に主成分分析を交えながら対処していく

使用データ

疑似的に作成した高校の中間テスト結果データ
文系科目：英語、現代文、古文、漢文、地理、倫理政経、現代社会、世界史、日本史
理系科目：数Ⅰ、数Ⅱ、数A、数B、生物、物理、有機化学、無機化学、地学

sample_size = 1000

# 乱数シードの固定
np.random.seed(1234)

# 全てのベースとなる総合学力データを生成
base = np.random.randint(10,100,sample_size)

# その他ベースとなる学力データを作成(総合学力が高い人は、その他のベース学力も高くなるように)
error_langbase = np.random.randint(5,30,sample_size)
lang_base = 0.7*base + error_langbase

error_socibase = np.random.randint(5,30,sample_size)
soci_base = 0.7*base + error_socibase

error_mathbase = np.random.randint(5,30,sample_size)
math_base = 0.7*base + error_mathbase

error_scibase = np.random.randint(5,30,sample_size)
sci_base = 0.7*base + error_scibase


# 現代文、英語、古文、漢文データの生成
## 現代文は独自30%とlang_baseを70%反映（現代文は比較的高得点者が多い）
modern_japanese = 0.3*np.random.randint(60,100,sample_size) + 0.7*lang_base

## 英語は独自50%とlang_baseを50%反映
english = 0.5*np.random.randint(5,100,sample_size) + 0.5*lang_base

## 古文は独自50%とlang_baseを50%反映
ancient_literature = 0.5*np.random.randint(30,100,sample_size) + 0.5*lang_base

## 漢文は独自20%と古文を70%反映（古文得意な人は漢文も得意の傾向にあるため）
chinese_literature = 0.2*np.random.randint(30,100,sample_size) + 0.8*ancient_literature


# 地理、倫理政経データの生成
## 地理は独自40%とsoci_baseを60%反映
geography =  0.4*np.random.randint(5,100,sample_size) + 0.6*soci_base

## 倫理は独自40%とsoci_baseを60%反映（倫理は比較的高得点者が多い）
ethics =  0.4*np.random.randint(60,100,sample_size) + 0.6*soci_base

# 現代社会、日本史、世界史データの生成（現代社会は比較的高得点者が多い）
## 現代社会は独自20%とsoci_baseを80%反映
modern_society = 0.2*np.random.randint(60,100,sample_size) + 0.8*soci_base

## 日本史は独自70%とsoci_baseを30%反映
japanese_history = 0.6*np.random.randint(30,100,sample_size) + 0.2*soci_base + 0.2*modern_society

## 世界史は独自30%と地理×現代社会の70%を反映
world_history = 0.3*np.random.randint(30,100,sample_size) + (geography*modern_society)*(1/10000)*100*0.7


## 数１、数２、数A、数Bデータを生成
## 数1は独自30%とmath_baseを70%反映
math1 = 0.3*np.random.randint(30,100,sample_size) + 0.7*math_base

## 数2は独自40%と数1を30%とmath_baseを20%反映
math2 = 0.4*np.random.randint(30,100,sample_size) + 0.3*math1 + 0.2*math_base

## 数Aは独自30%とmath_baseを70%反映
mathA = 0.3*np.random.randint(5,100,sample_size) + 0.7*math_base

## 数Bは独自50%と数Aを40%とmath_baseを10%反映
mathB = 0.5*np.random.randint(30,100,sample_size) + 0.4*mathA + 0.1*math_base

# 物理、地学データを生成
## 物理は独自30%とmath_base×sci_baseの70%を反映
physics =  0.3*np.random.randint(5,100,sample_size) + (math_base*sci_base)*(1/10000)*100*0.7

## 地学は独自30%と物理を50%とmath_base20%を反映
geology =  0.3*np.random.randint(5,100,sample_size) + 0.5*physics + 0.2*math_base

# 生物、有機化学、無機化学データを生成
## 生物は独自40%とsci_base60%を反映
biological = 0.4*np.random.randint(5,100,sample_size) + 0.6*sci_base

## 有機化学は独自30%とsci_base60%を反映
organic_chemistry = 0.5*np.random.randint(10,100,sample_size) + 0.5*sci_base

## 無機化学は独自30%と有機化学30%とsci_base40%を反映
inorganic_chemistry = 0.3*np.random.randint(10,100,sample_size) + 0.3*organic_chemistry + 0.4*sci_base

data = pd.DataFrame({'現代文':modern_japanese,
                     '英語':english,
                     '古文':ancient_literature,
                     '漢文':chinese_literature,
                     '地理':geography,
                     '倫理政経':ethics,
                     '現代社会':modern_society,
                     '日本史':japanese_history,
                     '世界史':world_history,
                     '数1':math1,
                     '数2':math2,
                     '数A':mathA,
                     '数B':mathB,
                     '物理':physics,
                     '地学':geology,
                     '生物':biological,
                     '有機化学':organic_chemistry,
                     '無機化学':inorganic_chemistry})


# 予測対象を作成（期末の成績（３段階評価））：ベースの学力から区分
target = pd.DataFrame(base,columns=['期末成績'])
target.loc[target['期末成績']<45,'期末成績'] = 1
target.loc[(target['期末成績']>=45)&(target['期末成績']<75),'期末成績'] = 2
target.loc[target['期末成績']>=75,'期末成績'] = 3
data = pd.concat([data,target],axis=1)

data = data.astype(int)

• 生成したデータ件数
  1000件（1000人分）
• 期末成績別の割合
  成績1：全体の35.4%
  成績2：全体の35.6%
  成績3：全体の29%

# 後半で予測を行ってみるので学習データ（train）とテストデータ（test）に分割
X_train, X_test, y_train, y_test = train_test_split(data.drop('期末成績',axis=1), data['期末成績'], test_size = 0.2, random_state=123,stratify = data['期末成績'])

# 後ほど使いやすいので、X_trainとy_trainを結合
train_data = pd.concat([X_train,y_train],axis=1)
train_data.reset_index(drop=True,inplace=True)

# 後ほど使いやすいので、X_testとy_testを結合
test_data = pd.concat([X_test,y_test],axis=1)
test_data.reset_index(drop=True,inplace=True)

# 相関行列の作成
plt.figure(figsize=(10, 8))
sns.heatmap(train_data.corr(),annot=True, fmt='.2f',cmap='GnBu')

ミニマムのような理系・文系のような括りではなく、古文が得意であれば漢文も得意、数1が得意であれば数2も得意のような観点で作成している。意図せず倫理政経・現社と物理、数学に強い相関が見られるが「経済得意な人は理数の観点も必要なので得意」ということにしておく

累積寄与率を算出

第n主成分まで作成するか検討する

train_data_tmp = train_data.drop('期末成績',axis=1)
n_list = []
sum_ev_ratio_list = []

for n in range(len(train_data_tmp.columns)):
    
    pca = PCA(n_components = n)
    pca.fit(train_data_tmp)
    
    columns = []
    for c in range(n):
        col = 'component_' + str(c+1)
        columns.append(col)

    # 累積寄与率
    ev_ratio =  pd.DataFrame(pca.explained_variance_ratio_,index=columns,columns=['寄与率'])
    sum_ev_ratio = sum(ev_ratio['寄与率'])
    
    n_list.append(n)
    sum_ev_ratio_list.append(sum_ev_ratio)
    
plt.figure(figsize=(7,3))
plt.scatter(n_list,sum_ev_ratio_list)
plt.plot(n_list,sum_ev_ratio_list)
plt.plot([min(n_list),max(n_list)],[0.8,0.8],linestyle='--',color='red')
plt.title('累積寄与率')
plt.xlabel('n')
plt.ylabel('累積寄与率')
plt.grid()
plt.xticks(n_list)
plt.show()

第6主成分まであれば累積寄与率>=80%となることがわかるため、今回は第6主成分までを作成する

主成分得点・主成分負荷量の算出（PCA）

# 主成分得点
n = 6 # 作成する主成分の数
pca = PCA(n_components = n) #n_components = 何次元のデータに圧縮するか
pca.fit(train_data_tmp)
result = pca.transform(train_data_tmp)

columns = []
for c in range(n):
    col = 'component_' + str(c+1)
    columns.append(col)
    
result = pd.DataFrame(result,columns=columns)


# 主成分負荷量
eigen_vector = pca.components_
eigen_vector = pd.DataFrame(eigen_vector,index=columns,columns=train_data_tmp.columns).T


# 主成分負荷量の可視化
plt.figure(figsize=(10, 8))
sns.heatmap(eigen_vector,annot=True, fmt='.2f',cmap='GnBu')

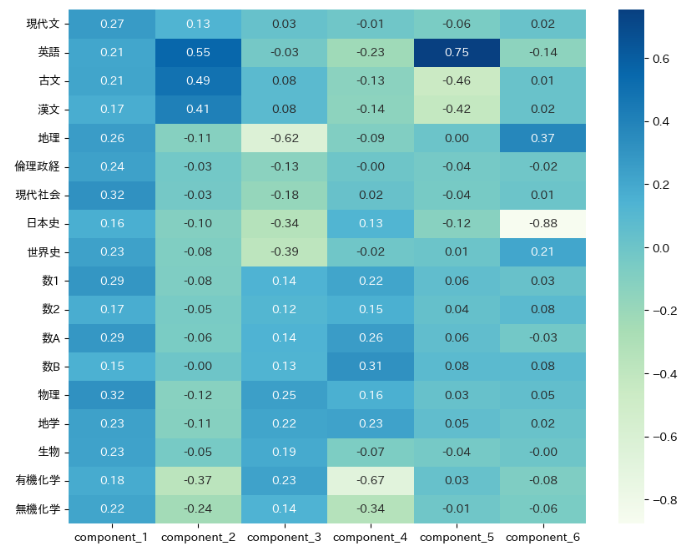
各主成分に解釈性を与えてみる（ざっくり強引に。）

• 第1主成分：地頭の良さ
• 第2主成分：言語・読解能力
• 第3主成分：文理特化力
• 第4主成分：数理能力
• 第5主成分：英語能力
• 第6主成分：暗記能力

期末成績の予測モデル

主成分を使用した「主成分回帰モデル」と「各科目をそのまま説明変数とした回帰モデル」で期末成績の予測精度を比較してみる

各科目をそのまま説明変数とした回帰モデル

• どの変数が期末成績に影響を与えているか見たいので、多重共線性の影響は取り除く
• VIF<10になるよう変数選択を実施（過程は本筋でないので省略）
• 順序ロジットモデルを使用
• 精度比較には正解率を採用

# 説明変数、被説明変数を変数y,Xに格納
y = train_data['期末成績']
X = train_data[['英語','物理']]

# モデルの構築
logit_od = OrderedModel(y,X,distr='logit')
reg_result = logit_od.fit(method='bfgs',disp=False)

# 結果を表示
display(reg_result.summary())

多重共線性の影響を除いた結果、2変数のみのモデルになったが、物理＞英語の順で期末成績に影響していることがわかる（p＜0.01）。本モデルを使用した学習データでの精度、テストデータでの精度（Accuracy）を以下に示した。

学習データ	テストデータ
0.74	0.76

主成分回帰モデル

• 主成分同士に多重共線性は発生しない
• 順序ロジットモデルを使用
• 精度比較には正解率を採用

train_data_tmp = result.copy()
train_data_tmp = pd.concat([train_data_tmp,train_data['期末成績']],axis=1)

# 説明変数、被説明変数を変数y,Xに格納
y = train_data_tmp['期末成績']
X = train_data_tmp.drop('期末成績',axis=1)

# モデルの構築
logit_od = OrderedModel(y,X,distr='logit')
reg_result = logit_od.fit(method='bfgs',disp=False)

# 結果を表示
display(reg_result.summary())

主成分4＞主成分1の順で期末成績に影響していることがわかる（p＜0.01）。本モデルを使用した学習データでの精度、テストデータでの精度（Accuracy）を以下に示した。

学習データ	テストデータ
0.88	0.91

• 主成分モデルでは、主成分同士で多重共線性は発生しない（主成分同士は直交する）。そのため、作成した主成分全ての情報量を使用してモデル作成ができ、その結果、多くの変数削除が必要になった「各科目をそのまま説明変数とした回帰モデル」と比べ、高い予測精度を発揮できている。

• 主成分モデルでは、変数の次元削除を行い「〇主成分」としての解釈性を与えており、分析者の定義付けによって、モデルの解釈は異なってしまうことから注意が必要である。今回の場合を強引に解釈すると、主成分4は「数理能力」、主成分1は「地頭の良さ」としたため、期末成績が高くなる人の要因は特に上記2つであると思われる、程度に留める。

まとめ

本記事を通して、主成分分析の目的や手法を説明してきた。また、作成した主成分の解釈が必要になる場合、分析者の定義付けに委ねられることは注意しなければならない。
本記事がこれから機械学習や主成分分析の学習をされる方の一助になれば嬉しいです。