本記事の目的
ARMA系モデル等の時系列分析を学習してきたので、備忘録としてまとめようと思います。まだ学習途中であり、不足する内容があるかもしれませんが、閲覧いただいた方の参考になればと思います。
分析の流れ
- データ構造の確認（Topic：自己相関 / 成分分解 / 定常性）
- 分析モデルの決定（Topic：各種時系列モデル）
- モデルの評価とチューニング
- モデルを使用した分析や予測タスク
主なライブラリ
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
import statsmodels.api as sm
import japanize_matplotlib
使用データ
今回は$CO_2$のデータセットを使用していきます。このデータセットは米国ハワイ州マウナロア天文台で収集された1958年3月～2001年12月の$CO_2$濃度が格納されています。
Mauna Loa Weekly Atmospheric CO2 Data
import statsmodels.datasets.co2 as co2
co2_data = co2.load().data
df = co2_data.resample('M').mean()
# 1958~1964年まで欠損が含まれるため、今回は1965年以降のデータを対象
df = df.iloc[82:]
df.index.name = 'year'
# 可視化
plt.figure(figsize=(10,3))
df['co2'].plot(c='blue')
plt.show()
明らかに上昇トレンドがありそうですね。
データ構造の確認
自己相関
まずは、の確認ということで、「自己相関」、「偏自己相関」を見ていきたいと思います。
自己相関はざっくり言うと、現在の自分に過去の自分がどの程度相関しているかを見る方法になります。ここでどのくらい過去の自分なのか、についてはLag(ラグ)を用いて表します。使用しているデータセットは1ヶ月単位の粒度のため、例えばLag1の自己相関については「1ヶ月前の$CO_2$が当月の$CO_2$とどの程度相関しているか」、Lag2の自己相関については「2ヶ月前の$CO_2$が当月の$CO_2$とどの程度相関しているか」を表しています。
偏自己相関は、原系列$Y_t$とLag系列$Y_{t-h}$の自己相関から、その間にあるLag系列$Y_{t-1}$~$Y_{t-h+1}$の影響を取り除いたものになります。例えば、原系列とLag3との偏自己相関については、Lag1~Lag2の影響を取り除く必要があります。
自己相関や偏自己相関を可視化したものを「コレログラム」と言い、データの周期性を捉えることができます。また、後述するAR系モデルでは自己相関がないと、うまく予測できないので、この確認は非常に重要なプロセスです。
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# コレログラム
fig, ax = plt.subplots(2, 1, figsize=(10,6))
# 自己相関係数
plot_acf (df['co2'], lags=50, ax=ax[0])
# 偏自己相関係数
plot_pacf(df['co2'], lags=50, ax=ax[1])
plt.xlabel('Lag')
plt.tight_layout()
plt.show()
コレログラムの偏自己相関を見てみると、Lag1との偏自己相関が強く、また、12ヶ月ごとに同じ変動パターンを繰り返しているため、周期は12ヶ月であるとわかります。
成分分解
コレログラムで周期がわかりましたので、ここからは原系列を「トレンド成分」、「季節成分」、「残差（原型列-トレンド成分-季節成分）」に分解していきます。手法はSTL分解（Seasonal Decomposition Of Time Series By Loess）を使用していきます。
fig, ax = plt.subplots(4, 1, figsize=(15, 12), sharex=True)
# period：周期を表すハイパーパラメータ
# 今回は月単位のデータであり、前提として1年（12ヶ月）周期の可能性あり
# 上記及びコレログラムより周期を12と指定
stl = sm.tsa.STL(df['co2'],period=12).fit()
df['co2'].plot(ax=ax[0], c='blue')
ax[0].set_title('原系列')
stl.trend.plot(ax=ax[1], c='cyan')
ax[1].set_title('トレンド成分')
stl.seasonal.plot(ax=ax[2], c='orange')
ax[2].set_title('季節成分')
stl.resid.plot(ax=ax[3], c='grey')
ax[3].set_title('残差')
plt.tight_layout()
plt.show()
成分分解結果を見てみると、上昇トレンドと季節周期を含んでいることがわかる。また、原系列はトレンド成分でほとんど構成されていおり、季節成分の構成は小さい。加えて、残差に特定のパターンも見られないため、うまく分解できていると思われる。また、（このグラフ粒度だとわかりにくいが）季節周期は12ヶ月であるとわかる。
定常性
時系列分析を行う上で定常性の確認は重要です。「定常である」か「定常でない（非定常）」か、によって前処理が発生、使用するモデルのハイパーパラメータ設定が変わってきます。
定常性には「弱定常性」と「強定常性」があり、時系列分析で「定常性」という場合は前者の「弱定常性」を意味していることが多いようです。
弱定常性
弱定常性は以下の2式で定義されます。
E(\,y_t\,) = μ・・・A
Cov(\,y_t , y_{t-j}\,) = γ_j・・・B
A：どの時点$y_t$においても平均が$μ$となり一定である
B：どの時点$y_t$においてもLag$j$との自己共分散※が$γ_j$であり、時点$t$に依存せずLag$j$にのみ依存する
「どの時点$y_t$においても平均が一定」というのはイメージが難しいと思います。一時点において観測されるデータは1つなのに、どうやって平均を出すのか、という疑問が出るかもしれません。これに対しては次のyoutube動画でわかりやすく解説してくれていましたので参考にさせていただきました（【時系列分析入門コース】まずは基礎をガッチリ固めてスタートダッシュ）。「一時点で観測されたデータは、その時点の背後に何らかの確率分布が存在し、あくまでもその確率分布から得られた1つの観測データであるため、平均や分散が存在する」ということみたいです。
※自己相関で言い換えても良いと思います。
「定常である」ことの重要性
データが「定常である」ことは、後述するAR系モデルの前提となっています。また、「定常でない」データを使用して作り上げた予測モデルに関しては、平均や自己相関が時点$t$によって変わってしまうため、将来においても同様に変わってしまい、過去と将来の一貫性がなく、将来予測が難しくなります。
つまり、モデル構築に使用したデータ（過去データ）が定常であれば、将来データに関してもその定常性は保たれると考えられるため、将来予測が可能になる、そのようなイメージです。
単位根
定常性に関連するものとして「単位根」というものが存在します。
時系列分析したいデータが常に「定常ある」ことは少ないと思います。少なからずトレンドを含んでいるなど非定常なことが多いのではないでしょうか。
単位根（過程）は、「原系列に1階差を取る」操作によって、定常性の仮定を満たすとき、原系列は単位根過程である、と言われます。
では、「原系列の1階差を取る」とは何か、次で見ていきます。
階差の取得
以下のような原系列があるとします（ここではわかりやすさ重視で$CO_2$データセットは使いません）。
| Date | Value |
|---|---|
| 7/1 | 10 |
| 7/2 | 7 |
| 7/3 | 12 |
| 7/4 | 15 |
| 7/5 | 5 |
ここで1階差とったカラムを追加してみます。この階差を取得した系列を「差分系列」と言います。
| Date | Value | 1階差 |
|---|---|---|
| 7/1 | 10 | |
| 7/2 | 7 | -3 |
| 7/3 | 12 | 5 |
| 7/4 | 15 | 3 |
| 7/5 | 5 | -10 |
つまり、「現在の値から1つ前の値の差分を取ること」=「1階差を取る」ことです。
差分系列で取る階差は1ではない場合もあります。例えば2階差取ってみます。
| Date | Value | 1階差 | 2階差 |
|---|---|---|---|
| 7/1 | 10 | ||
| 7/2 | 7 | -3 | |
| 7/3 | 12 | 5 | 8 |
| 7/4 | 15 | 3 | -2 |
| 7/5 | 5 | -10 | -13 |
つまり、「1階差の値に対しもう1階差取ること」=「2階差を取る」ことです。
1階差を取ることによって、定常性を満たす（＝単位根）ことの確認は、ARIMAやSARIMAを使用する際のハイパーパラメータの設定にも使用できます。その他、階差を取る前に対数変換を行う「対数差分系列」という方法もあります。
次ではどのように単位根（過程）を確認するのかを見ていきます。
単位根の検定（ADF検定：Augmented Dickey–Fuller test）
単位根の確認方法として「ADF検定」があります。帰無仮説、対立仮説は次のとおりです。
帰無仮説：データが単位根過程である（つまり階差取得前の原系列は非定常である）
対立仮説：データが定常である（つまり階差を取らずともでは定常である）
ここで思い出してほしいのは「原系列に1階差を取る」操作によって、定常性の仮定を満たす、場合に単位根である、ということ。つまり単位根である、ということは「階差を取らない場合、非定常である」ことになります。
ADF検定によって帰無仮説を棄却できた場合、「原系列は定常である」と判断し、棄却できない場合、「単位根であるため、階差取得等の操作によって定常なデータに変換が必要」と判断できます。
adf = sm.tsa.stattools.adfuller(df['co2'], regression='ct')
print('ADF統計量：{0} p値：{1}'.format(adf[0].round(3),adf[1].round(3)))
# regression：データ構造により以下から指定
# ctt・・・2次のトレンドあり＆定数項あり
# ct・・・1次のトレンドあり＆定数項あり
# c・・・トレンドなし＆定数項あり
# n・・・# トレンドなし＆定数項なし
ADF統計量：-2.706 p値：0.234
今回は成分分解によって、明らかに上昇トレンド※が確認できたので「1次のトレンドあり」、及び可視化から定数項が0でないと明らかなので「定数項あり」の'ct'をregressionに指定しています。
ここでは有意水準を5%として結果を解釈すると、p>0.05のため、帰無仮説を棄却できず、「データが単位根である」ということになります。
※トレンド有無の確認に「Mann-Kendall trend test」という検定方法もありますので、次で触れます。
トレンドの検定
トレンド有無の検定方法についても紹介します。帰無仮説、対立仮説は次のとおりです。
帰無仮説：トレンドは存在しない
対立仮説：トレンドが存在する
!pip install pymannkendall
import pymannkendall as mk
mkt = mk.original_test(df['co2'])
print('トレンド：{0} 判定：{1} p値：{2}'.format(mkt[0],mkt[1],mkt[2].round(3)))
トレンド：increasing 判定：True p値：0.0
ここでは有意水準を5%として結果を解釈すると、p<0.05のため、帰無仮説を棄却し、「データにトレンドが存在する」ということになります。
データ構造の確認まとめ
- コレログラムより、原系列と強い相関を持つLagが確認されたため、予測可能である可能性が高い
- 成分分解より、上昇トレンド、季節周期（12ヶ月）が存在する
- ADF検定から、原系列は単位根であると確認したため、階差取得が必要である
各種時系列モデル
ホワイトノイズ（W.N）
始めに「ホワイトノイズ」について記載します。
ホワイトノイズは、ざっくり言うと「時系列データ特有の特別なノイズ」です。
時系列モデルの場合、真の回帰式の誤差項はホワイトノイズで表されます。
ホワイトノイズは以下の3式で定義されます。
E(\,ε_t\,) = 0・・・A
Var(\,ε_t\,) = σ^2・・・B
Cov(\,ε_t , ε_{t-j}\,) = 0・・・C
A：どの時点の誤差$ε_t$においても平均が0である
B：どの時点の誤差$ε_t$においても分散が一定である
C：どの時点の誤差$ε_t$においてもLag$j$との自己共分散が0である
イメージしにくいですが、「どの時点$t$においても$ε_t$の平均が0、分散が一定」というのは定常性と同じ考え方で良いと思います。また、いかなるLagにおいても自己共分散が0のため、ホワイトノイズ（ホワイトノイズのみで構成される時系列データ）は、どのLagにおいても自己相関が0になります。
ホワイトノイズの定常性については、「どの時点においても平均が$μ$となり一定である」「どの時点においてもLag$j$との自己共分散※が$γ_j$である」という定常性の仮定を満たしているため、ホワイトノイズ（ホワイトノイズのみで構成される時系列データ）は「定常である」ことがわかります。
データ構造による時系列モデルの選定
| データ構造 | 定常性あり | 自己相関あり | ホワイトノイズあり | 季節周期あり | 外生変数あり |
|---|---|---|---|---|---|
| AR | 〇 | 〇 | |||
| MA | 〇 | 〇 | |||
| ARMA | 〇 | 〇 | 〇 | ||
| ARIMA | 〇※ | 〇 | 〇 | ||
| ARIMAX | 〇※ | 〇 | 〇 | 〇 | |
| SARIMA | 〇※ | 〇 | 〇 | 〇 | |
| SARIMAX | 〇※ | 〇 | 〇 | 〇 | 〇 |
※原系列のデータが非定常であっても利用可能（モデル内で階差を取るため）
データ分割
モデルの確認で使用していくため、「1階差を取得し定常に変換したデータ」と「原系列のままのデータ」の2種類を用意し、さらにモデル構築用の学習データとテストデータに分割していきます。
# 差分系列の作成（1階差）
df_diff = df['co2'].diff(periods=1).dropna()
df_diff = pd.DataFrame(df_diff)
# dfを学習用とテスト用に分割
train_size_original = 300 # 前から300件(25年分)のデータを使用
test_size_original = len(df) - train_size_original
train_original = df.iloc[:train_size_original]
test_original = df.iloc[train_size_original:]
# df_diffを学習用とテスト用に分割
train_size_diff = 300 # 前から300件(25年分)のデータを使用
test_size_diff = len(df_diff) - train_size_diff
train_diff = df_diff.iloc[:train_size_diff]
test_diff = df_diff.iloc[train_size_diff:]
# 分割結果を可視化
fig = plt.figure(figsize=(10,7))
ax1 = fig.add_subplot(2,1,1)
train_original['co2'].plot(ax=ax1,c='blue')
test_original['co2'].plot(ax=ax1,c='green')
ax2 = fig.add_subplot(2,1,2)
train_diff['co2'].plot(ax=ax2,c='blue')
test_diff['co2'].plot(ax=ax2,c='green')
ax1.set_title('原系列')
ax2.set_title('階差系列')
ax1.set_xlabel(None)
ax2.set_xlabel(None)
plt.show()
青がモデル作成用データ、緑がテスト用データ
次のAR~ARMAでは階差系列を、ARIMA~SARIMAでは原系列を使用していきます。
ハイパーパラメータ探索を行う関数
今回は2~3個の中から最適なハイパーパラメータを探索していきます。
# AICでモデル評価を行う関数を生成
def search_params(endog ,
exog ,
p_list ,
d_list ,
q_list ,
P_list ,
D_list ,
Q_list ,
m_list) :
result_list = []
for p in p_list:
for d in d_list:
for q in q_list:
for P in P_list:
for D in D_list:
for Q in Q_list:
for m in m_list:
try:
model = sm.tsa.SARIMAX(endog = endog,
exog = exog,
order=(p, d, q),
seasonal_order=(P, D, Q, m)).fit(maxiter=1000 ,disp=False)
aic_value = model.aic
results = [p,d,q,P,D,Q,m,aic_value]
result_list.append(results)
except:
aic_value = np.nan
results = [p,d,q,P,D,Q,m,aic_value]
result_df = pd.DataFrame(result_list,columns=['p','d','q','P','D','Q','m','aic'])
display(result_df[result_df['aic']==result_df['aic'].min()])
テストデータと予測値をプロットする関数
# テストデータと予測値比較用の関数を作成
def plot_test(test ,pred) :
pred = pd.Series(pred ,index=test.index)
plt.figure(figsize=(12,3))
test.plot(label='Test')
pred.plot(label='Pred')
plt.legend(loc='upper left')
plt.show()
AR：Auto Regressive（自己回帰モデル）
- 自己回帰という用語は自分自身を自分自身で回帰するということ
- 現在の値は過去の自分自身の値のみに影響を受ける、としたモデル
- 定常過程でのみ適用可能なモデルのため、非定常なデータは定常にする必要あり
回帰式 AR(p)：p次のARモデル
y_t = c + φ_1y_{t-1} + φ_2y_{t-2} + ・・・ φ_py_{t-p} + ε_t
$c$：定数項、$φ$：回帰係数、$ε$：ホワイトノイズ
search_params(endog = train_diff,
exog = None ,
p_list = [3,5,10] ,
d_list = [0] ,
q_list = [0] ,
P_list = [0] ,
D_list = [0] ,
Q_list = [0] ,
m_list = [0] )
ハイパーパラメータ探索結果
| p | d | q | P | D | Q | m | aic |
|---|---|---|---|---|---|---|---|
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 479.553927 |
ar_model = sm.tsa.SARIMAX(endog = train_diff, order=(10, 0, 0)).fit(maxiter=1000 ,disp=False)
# 予測値を算出
test_pred = pd.Series(ar_model.forecast(test_size_diff), index=test_diff.index)
# 観測値と予測値をプロット
plot_test(test = test_diff['co2'] ,pred = test_pred)
# 残差の確認
plt.rcParams['figure.figsize'] = (12, 8)
ar_model.plot_diagnostics(lags=30)
plt.show()
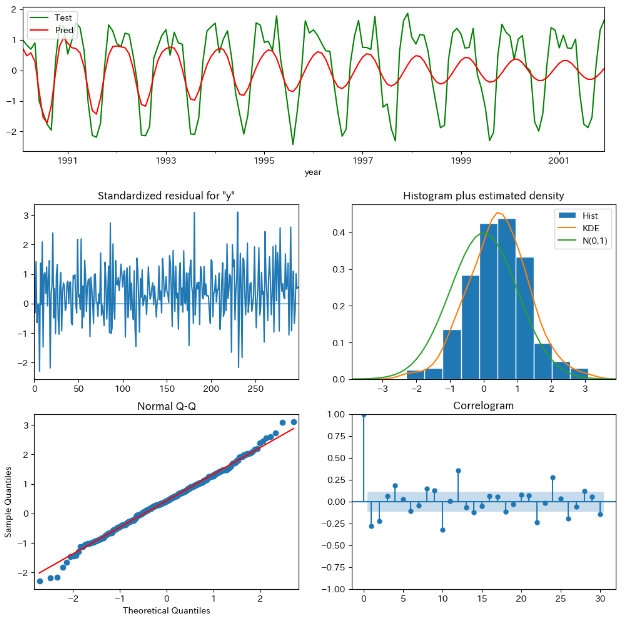
テストデータをうまく予測できていないとわかります。また、モデルの方では残差に自己相関が存在しています。うまく予測できていれば残差はホワイトノイズ（自己相関は0）になるはずなので、モデルがデータの特徴を捉えられていないとわかります。
MA：Moving Average（移動平均モデル）
- 現在の値は過去のホワイトノイズのみに影響を受ける、としたモデル
- 定常過程でのみ適用可能なモデルのため、非定常なデータは定常にする必要あり
回帰式 MA(q)：q次のMAモデル
y_t = c + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2} + ・・・ θ_qε_{t-q}
$c$：定数項、$θ$：回帰係数、$ε$：ホワイトノイズ
search_params(endog = train_diff,
exog = None ,
p_list = [0] ,
d_list = [0] ,
q_list = [3,5,10] ,
P_list = [0] ,
D_list = [0] ,
Q_list = [0] ,
m_list = [0] )
ハイパーパラメータ探索結果
| p | d | q | P | D | Q | m | aic |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 10 | 0 | 0 | 0 | 0 | 553.373732 |
ma_model = sm.tsa.SARIMAX(endog = train_diff, order=(0, 0, 10)).fit(maxiter=1000 ,disp=False)
# 予測値を算出
test_pred = pd.Series(ma_model.forecast(test_size_diff), index=test_diff.index)
# 観測値と予測値をプロット
plot_test(test = test_diff['co2'] ,pred = test_pred)
# 残差の確認
plt.rcParams['figure.figsize'] = (12, 8)
ma_model.plot_diagnostics(lags=30)
plt.show()
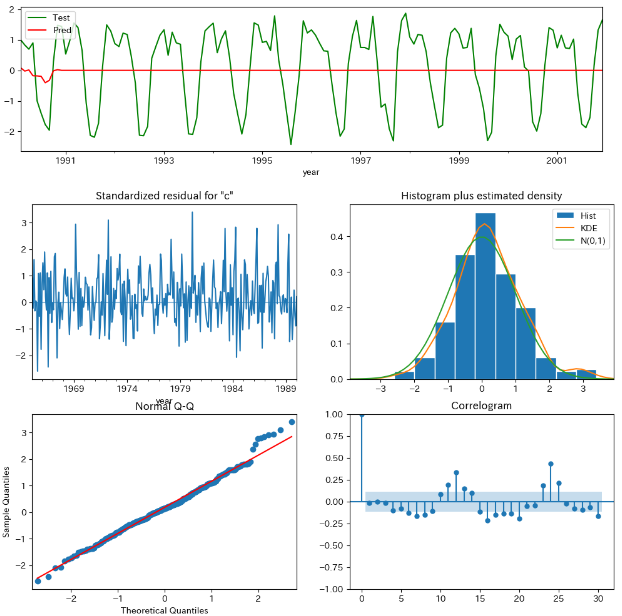
テストデータをまったく予測できていないとわかります。また、モデルの方では残差に自己相関が存在しているだけでなく、周期的な変動も含まれており、モデルが全くデータの特徴を捉えられておらず、ほとんど残差に落ちてしまっているとわかります。
ARMA：Auto Regressive Moving Average（自己回帰移動平均モデル）
- ARとMAを合体させたモデル
- 現在の値は過去の自分自身の値とホワイトノイズのみに影響を受ける、としたモデル
- 定常過程でのみ適用可能なモデルのため、非定常なデータは定常にする必要あり
回帰式 ARMA(p,q)：p,q次のARMAモデル
y_t = c + φ_1y_{t-1} + φ_2y_{t-2} + ・・・ φ_py_{t-p} + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2} + ・・・ θ_qε_{t-q}
$c$：定数項、$θ$：回帰係数、$ε$：ホワイトノイズ
search_params(endog = train_diff,
exog = None ,
p_list = [3,5,10] ,
d_list = [0] ,
q_list = [3,5,10] ,
P_list = [0] ,
D_list = [0] ,
Q_list = [0] ,
m_list = [0] )
ハイパーパラメータ探索結果
| p | d | q | P | D | Q | m | aic |
|---|---|---|---|---|---|---|---|
| 10 | 0 | 10 | 0 | 0 | 0 | 0 | 200.793482 |
arma_model = sm.tsa.SARIMAX(endog = train_diff, order=(10, 0, 10)).fit(maxiter=1000 ,disp=False)
# 予測値を算出
test_pred = pd.Series(arma_model.forecast(test_size_diff), index=test_diff.index)
# 観測値と予測値をプロット
plot_test(test = test_diff['co2'] ,pred = test_pred)
# 残差の確認
plt.rcParams['figure.figsize'] = (12, 8)
arma_model.plot_diagnostics(lags=30)
plt.show()
ARやMAに比べ、テストデータを大分予測できています。また、モデルの方では残差にほとんど自己相関もなくなっていることがわかります。
ARIMA：Auto Regressive Integrated Moving Average（自己回帰和分移動平均モデル）
- 現在の差分系列は過去の差分系列の値とホワイトノイズのみに影響を受ける、としたモデル
- モデル内のハイパーパラメータ$d$により原系列に$d$階差を取り、非定常過程にも適用可能にしたモデル（原系列に$d$階差取った差分系列は、定常である必要あり）
- 階差を取らない場合（$d$=0）のARIMA(p,0,q)は、ARMAと同義である
回帰式 ARIMA(p,d,q)：p,d,q次のARIMAモデル
y^{'}_t = c + φ_1y^{'}_{t-1} + φ_2y^{'}_{t-2} + ・・・ φ_py^{'}_{t-p} + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2} + ・・・ θ_qε_{t-q}
$y^{'}$：$d$階差を取った差分系列、$c$：定数項、$θ$：回帰係数、$ε$：ホワイトノイズ
search_params(endog = train_original,
exog = None ,
p_list = [3,5,10] ,
d_list = [0,1,2] ,
q_list = [3,5,10] ,
P_list = [0] ,
D_list = [0] ,
Q_list = [0] ,
m_list = [0] )
ハイパーパラメータ探索結果
( AIC=42が最小値であるが、エラー検出のため対象外 )
| p | d | q | P | D | Q | m | aic |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 10 | 0 | 0 | 0 | 0 | 173.830542 |
arima_model = sm.tsa.SARIMAX(train_original, order=(10, 1, 10)).fit(maxiter=1000 ,disp=False)
# 予測値を算出
test_pred = pd.Series(arima_model.forecast(test_size_original), index=test_original.index)
# 観測値と予測値をプロット
plot_test(test = test_original['co2'] ,pred = test_pred)
# 残差の確認
plt.rcParams['figure.figsize'] = (12, 8)
arima_model.plot_diagnostics(lags=30)
plt.show()
ARMA同様に良く予測できており、ARIMAが非定常な原系列に対し対応可能であることもわかります。
SARIMA：Seasonal Auto Regressive Integrated Moving Average（季節自己回帰和分移動平均モデル）
- ARIMAを季節周期方向に拡張したモデル
- SARIMA(p,d,q)(P,D,Q)mで表す
- (p,d,q)についてはARIMAと同義であり、(P,D,Q)はそれぞれ季節成分に対し(p,d,q)と同義であり、mは季節周期である
- 回帰式がAR~ARIMAに比べ多少複雑でありB（Backshift Operator：後退オペレーター）を用いて表現される
Backshit Operator（後退オペレーター）：
Backshit Operatorは、例えば$Y_t$に作用させることで、その一つ前の状態$Y_{t−1}$を返す演算子になります。
以降、Backshit OperatorをBと表記します。
とある時系列Yが存在する
Y_t = Y_1,Y_2,Y_3,...
Bは以下のように定義される
Y_{t-1} = BY_t
例1）ARモデルをBを用いて表現した場合：
Y_t = φ_1Y_{t-1} + φ_2Y_{t-2} + ・・・ φ_pY_{t-p} + ε_t
$Y_{t-1} = BY_t$であることから
Y_t = φ_1BY_t + φ_2B(\,BY_t\,) + ・・・ φ_pB^{p}\,Y_t + ε_t
右辺に$ε_t$のみを残す
Y_t - (\, φ_1BY_t + φ_2B(\,BY_t\,) + ・・・ φ_pB^{p} Y_t \,) = ε_t
左辺を$Y_t$でまとめる
1 - (\, φ_1 + φ_2B^{2} + ・・・ φ_pB^{p} \,)Y_t = ε_t
$φ(B) = 1 - (, φ_1 + φ_2B^{2} + ・・・ φ_pB^{p} ,)$とおくと
φ(B)Y_t = ε_t
$where$
φ(B) = 1 - (\, φ_1 + φ_2B^{2} + ・・・ φ_pB^{p} \,) = 1 - \sum_{k=1}^{p}φ_k\,B^k
例2）MAモデルをBを用いて表現した場合：
Y_t = ε_t + θ_1ε_{t-1} + θ_2ε_{t-2} + ・・・ θ_qε_{t-q}
$ε_{t-1} = Bε_t$であることから
Y_t = ε_t + θ_1Bε_t + θ_2B(\,Bε_t\,) + ・・・ θ_qB^{q} ε_t
左辺を$ε_t$でまとめる
Y_t = (\, 1 + θ_1B + θ_2B^{2} + ・・・ θ_qB^{q} \,)ε_t
$θ(B) = 1 + θ_1B + θ_2B^{2} + ・・・ θ_qB^{q}$とおくと
Y_t = θ(B)ε_t
$where$
θ(B) = 1 + θ_1 + θ_2B^{2} + ・・・ θ_qB^{q} = 1 + \sum_{k=1}^{q}θ_kB^k
例3）ARMAモデルをBを用いて表現した場合：
Y_t = φ_1Y_{t-1} + φ_2Y_{t-2} + ・・・ φ_py_{t-p} + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2} + ・・・ θ_qε_{t-q}
$Σ$で表記すると
Y_t = \sum_{k=1}^{p}φ_kY_{t-k} + ε_t + \sum_{k=1}^{q}θ_kε_{t-k}
$\sum_{k=1}^{p}φ_kY_{t-k}$を左辺に移行し
Y_t - \sum_{k=1}^{p}φ_kY_{t-k} \,= ε_t + \sum_{k=1}^{q}θ_kε_{t-k}
Bを用いて表現すると
Y_t - \sum_{k=1}^{p}φ_kB^{k}\,Y_t \,= ε_t + \sum_{k=1}^{q}θ_kB^{k}\,ε_t
左辺を$Y_t$、右辺を$ε_t$でまとめる
(\, 1 - \sum_{k=1}^{p}φ_kB^{k} \,)Y_t \,= (\, 1 + \sum_{k=1}^{q}θ_kB^{k} \,)ε_t
()内をそれぞれ、$φ(B)$、$θ(B)$と置くと
φ(B)Y_t = θ(B)ε_t
$where$
φ(B) = 1 - \sum_{k=1}^{p}φ_kB^k
θ(B) = 1 + \sum_{k=1}^{q}θ_kB^k
例4）差分系列をBを用いて表現した場合：
ここで$Y_{t-1}$は以下であった
Y_{t-1} = BY_t
1階差のとき
\begin{align}
Y^{'}_t &= Y_t - Y_{t-1}\\
&= Y_t - BY_{t}\\
&= ( 1 - B)Y_t
\end{align}
2階差のとき
\begin{align}
Y^{'}_t &= ( Y_t - Y_{t-1} ) - ( Y_{t-1} - Y_{t-2} )\\
&= ( 1 - B)Y_t - ( Y_{t-1} - BY_{t-1} )\\
&= ( 1 - B)Y_t - (1 - B)Y_{t-1}\\
&= ( 1 - B)(Y_t - Y_{t-1})\\
&= ( 1 - B)( 1 - B)Y_t\\
&= (1 - B)^{2}Y_t
\end{align}
d階差のとき
Y^{'}_t = (1 - B)^{d}Y_t
Backshit Operatorは次のリンク先で詳しくまとめられていましたので参考にさせていただきました。
時系列分析：後退オペレータについて
SARIMAモデルの回帰式
回帰式 SARIMA(p,d,q)(P,D,Q)s：
φ(B)\,Φ(B^{m})\,(1 -B)^{d}\,(1-B^{m})^{D}\,y_t = θ(B)\,Θ(B^{m})\,ε_t
$where$
φ(B) = 1 - \sum_{k=1}^{p}φ_kB^{k}・・・A
Φ(B) = 1 - \sum_{k=1}^{P}Φ_kB^{km}・・・B
θ(B) = 1 + \sum_{k=1}^{q}θ_kB^{k}・・・C
Θ(B) = 1 + \sum_{k=1}^{Q}Θ_kB^{km}・・・D
A：階差$d$系列に対するAR(p)のこと
B：季節階差$D$系列に対するAR(P)のこと
C：階差$d$系列に対するMA(q)のこと
D：季節階差$D$系列に対するMA(Q)のこと
$(1 - B)^d$：系列に$d$階差を取る
$(1 - B^m)^D$：周期$m$の季節階差を系列に$D$回取る※
$φ$：階差$d$系列に対するARの回帰係数、$Φ$：季節階差$D$系列に対するARの回帰係数、$θ$：階差$d$系列に対するMAの回帰係数、$Θ$：季節階差$D$系列に対するMAの回帰係数
「例3）ARMAモデルをBを用いて表現した場合：」に季節階差系列の項が追加されただけであるとわかります。
※季節階差
「今季の時点t - 前季の時点t-m」が季節階差になります。例えば、12ヶ月周期の場合、今季の1月の値 - 前季の1月の値、今季の2月の値 - 前季の2月の値、・・・です。
sY^{'}_t = Y_t - Y_{t-m}
周期$m$で繰り返す時系列データにD回季節階差を取る、とは次のイメージです。
$m=12$とします。
| Year Month | 原系列 | 季節階差 D=1 | 季節階差 D=2 |
|---|---|---|---|
| 2020-01 | 10 | ||
| 2020-02 | 17 | ||
| ・・・ | ・・・ | ・・・ | ・・・ |
| 2020-11 | 20 | ||
| 2020-12 | 12 | ||
| 2021-01 | 14 | 4 | |
| 2021-02 | 20 | 3 | |
| ・・・ | ・・・ | ・・・ | ・・・ |
| 2021-11 | 24 | 4 | |
| 2021-12 | 13 | 1 | |
| 2022-01 | 19 | 5 | 1 |
| 2022-02 | 32 | 12 | 9 |
| ・・・ | ・・・ | ・・・ | ・・・ |
| 2022-11 | 28 | 4 | 0 |
| 2022-12 | 21 | 8 | 7 |
SARIMAの回帰式は次のリンク先で詳しくまとめられていましたので、参考にさせていただきました。
【ML Tech RPT. 】第17回 構造に関連する機械学習を学ぶ (3) ~時系列予測~
search_params(endog = train_original,
exog = None ,
p_list = [5,10] ,
d_list = [1,2] ,
q_list = [5,10] ,
P_list = [1,2] ,
D_list = [1,2] ,
Q_list = [1,2] ,
m_list = [12] )
ハイパーパラメータ探索結果
| p | d | q | P | D | Q | m | aic |
|---|---|---|---|---|---|---|---|
| 5 | 1 | 5 | 2 | 1 | 1 | 12 | 142.231067 |
sarima_model = sm.tsa.SARIMAX(train_original, order=(10, 1, 10),seasonal_order=(1, 1, 1, 12)).fit(maxiter=1000 ,disp=False)
# 予測値を算出
test_pred = pd.Series(sarima_model.forecast(test_size_original), index=test_original.index)
# 観測値と予測値をプロット
plot_test(test = test_original ,pred = test_pred)
# 残差の確認
plt.rcParams['figure.figsize'] = (10, 6)
sarima_model.plot_diagnostics(lags=30)
plt.show()
残差の自己相関がほとんど0に近くなっていることがわかります。また、ARIMAよりテストデータをうまく予測できていそうです。
ARIMAX / SARIMAX
ARIMAXやSARIMAXは外生変数を回帰式に取り込んだモデルです。時系列データ同士が互いに影響しあわない、または関係が不明な場合、外生変数と呼ぶ。
回帰式 ARIMAX(p,d,q)：
y^{'}_t = c + βx_t + φ_1y^{'}_{t-1} + φ_2y^{'}_{t-2} + ・・・ φ_py^{'}_{t-p} + ε_t + θ_1ε_{t-1} + θ_2ε_{t-2} + ・・・ θ_qε_{t-q}
$x_t$：外生変数、$β$：外生変数$x_t$の回帰係数
使用データ
$CO_2$のデータセットに外生変数を追加していきます。ここでは$CO_2$濃度は消費電力の増加する夏、冬に影響している、と仮定し、カテゴリ変数を作成します。日本で夏は6~8月、冬は12~2月ですが、時期が真逆の国もあるため、「summer」、「winter」というカラム名ではなく「jun_aug」と「dec_feb」で作成します。
# 外生変数「jun_aug」と「dec_feb」を追加
df['month'] = df.index
df['month'] = pd.to_datetime(df['month']).dt.strftime('%m').astype(int)
df['jun_aug'] = 0
df.loc[(df['month']>=6)&(df['month']<9),'jun_aug'] = 1
df['dec_feb'] = 0
df.loc[(df['month']==12)|(df['month']==1)|(df['month']==2),'dec_feb'] = 1
df = df.drop('month',axis=1)
# dfを学習用とテスト用に分割
train_size_original = 300 # 前から300件(25年分)のデータを使用
test_size_original = len(df) - train_size_original
train_original = df.iloc[:train_size_original]
test_original = df.iloc[train_size_original:]
これまでと同様にハイパーパラメータを探索していきます。
search_params(endog = train_original['co2'],
exog = train_original[['jun_aug','dec_feb']],
p_list = [3,5,10] ,
d_list = [0,1,2] ,
q_list = [3,5,10] ,
P_list = [0] ,
D_list = [0] ,
Q_list = [0] ,
m_list = [0] )
ハイパーパラメータ探索結果
( AIC=39が最小値であるが、エラー検出のため対象外 )
| p | d | q | P | D | Q | m | aic |
|---|---|---|---|---|---|---|---|
| 10 | 2 | 10 | 0 | 0 | 0 | 0 | 184.628349 |
arimax_model = sm.tsa.SARIMAX(endog = train_original['co2'],
exog = train_original[['jun_aug','dec_feb']],order=(10, 2, 10)).fit(maxiter=1000 ,disp=False)
# 予測値を算出
test_pred = pd.Series(arima_model.forecast(test_size_original , exog = test_original[['jun_aug','dec_feb']]), index=test_original.index)
# 観測値と予測値をプロット
plot_test(test = test_original['co2'] ,pred = test_pred)
# 残差の確認
plt.rcParams['figure.figsize'] = (12, 8)
arima_model.plot_diagnostics(lags=30)
plt.show()
予測結果にあまり変化は見られませんが、ARIMAと比較してモデルのAICが高くなってしまったので、不要な外生変数になってしまいました。
また、今回のような外生変数ではなく、互いに影響しあう複数の時系列データをモデルに組み込む際は、VARモデル等がありますが、次回のまとめにしようと思います。
Prophet
ProphetはMetaが公開している時系列データ予測ライブラリです。
個人的には処理速度が速いと思います。
今回はARIMAXで使用した外生変数ありのデータを使用していきます（特に外生変数はモデルに影響しなさそうですが、モデルへの投入例として）。
!pip install Prophet
from prophet import Prophet
# 日付カラム名をds、系列名をyに変更
train_forpf = train_original.copy()
train_forpf['YEAR'] = train_forpf.index
train_forpf.rename(columns={'co2':'y','YEAR':'ds'},inplace=True)
# モデルを構築
model = Prophet()
# 外生変数の追加指示
model.add_regressor('jun_aug')
model.add_regressor('dec_feb')
# 複数の外生変数を追加する際は以下のように記載
# model.add_regressor('A')
# model.add_regressor('B')
# model.add_regressor('C')
model.fit(train_forpf)
# データの粒度を引数に指定する必要あり（freq：デフォルトが１日ごとになっている。今回は月別データのためfreq='m'を指定）
future = model.make_future_dataframe(periods=test_size_original,freq='m') # m(月単位)でtest_size_original分のデータを予測
# futureには学習データ数＋ステップ数の日付データが格納されるため、外生変数についても学習分＋テスト分を格納する
df_ = df.copy()
df_['ds'] = df.index
df_ = df_[['ds','jun_aug','dec_feb']]
# futureに外生変数を結合
future = pd.merge(future , df_ ,on = 'ds' , how='inner')
forecast = model.predict(future)
# 観測値と予測値をプロット
fct_yhat = forecast[['yhat','ds']][train_size_original:train_size_original + test_size_original]
fct_yhat.index = fct_yhat['ds']
fct_yhat = fct_yhat.drop('ds',axis=1)
plot_test(test = test_original['co2'] ,pred = fct_yhat['yhat'])
# モデルの構成要素描画
model.plot_components(forecast)
plt.show()
ARIMA系に比べ、あまり予測できていないように思いますが、成分分解のメソッドがあるのは嬉しいです。今回チューニングしておりませんので、しっかりハイパーパラメータを探索していくことで精度向上は十分可能と思います。
以下の記事でProphetのハイパーパラメータチューニングがまとめられております！
Prophetでチューニングすべきパラメータ
まとめ
AR~SARIMAまでをさーっと記載してきました。今回は予測メインでしたがProphetのハイパーパラメータ探索や、状態空間モデルに触れられませんでしたので、別の機会に触れていこうと思います。またVARモデルを使用した複数時系列データのモデル投入、VARでの分析等は次回のテーマにしようと思います。