LoginSignup
1
1
@Takahiro_zzz(Takahiro)

【分析】傾向スコアを使用した処置効果の推定

Posted at

本記事の目的

  • 分析業務を始めてもなかなか取っつきづらい「傾向スコア」を理解する
  • 「傾向スコア」を使用したマッチング等による共変量の影響を極力取り除いた処置効果の推定方法を理解する

傾向スコア（Propensity Score）

  • 与えられた共変量（説明変数）において介入（処置）が行われる確率
    • 主にロジスティック回帰で確率推定をすることが多いが、共変量からの確率推定ができれば特に決まりはない
  • 傾向スコアを使用した介入効果の推定方法として、「傾向スコアマッチング（Propensity Score Matching）」や「IPTW（IPWとも言う。Inverse Probability of Treatment Weighting）」、「DR（Doubly Robust）法」、「傾向スコア層別解析」などが代表的である
  • 条件付き独立の仮定（CIA：Conditional Independence Assumption）が存在する
    • CIA
      • 傾向スコアP(Xi)で処置変数を条件付けたとき、処置変数（Zi）と結果変数（Yi）が独立
( Y_{0i},Y_{1i} ) ⊥ Z_i | P(X_{i})

傾向スコアマッチング（Propensity Score Matching）

  • 処置（介入）を受けた群（介入群、処置群）と受けていない群（対象群）を、各サンプルの処置を受ける傾向（傾向スコア＝処置を受ける確率）に基づいて、処置群と対象群のペアでマッチングさせる
  • マッチングさせたペアで差を算出し、全ペア差の平均値を介入効果の推定値とする
  • マッチングペアの作成方法
    • 強欲マッチング
      • 復元・非復元
        • 使用したサンプルの復元を許容する「復元マッチング」や許容しない「非復元マッチング」がある
      • ペア探索
        • 処置群のとあるサンプルiに最も近い傾向スコアを持つ対象群のサンプルi´をペアにする「最近傍マッチング」や一定のペア探索領域（キャリパー）を設定しそのキャリパー内で近傍マッチングを行う「キャリパー近傍マッチング」がある
    • 最適マッチング
      • マッチングするサンプル同士の傾向スコアの差（絶対値）の合計が最小になるようにペアを作成していく

IPTW（Inverse Probability of Treatment Weighting）

  • 逆確率重み付け法
  • 傾向スコアをサンプルの重みとして利用し、与えられたデータ全体での介入を受けた場合の期待値と、介入を受けなかった場合の期待値を推定する方法
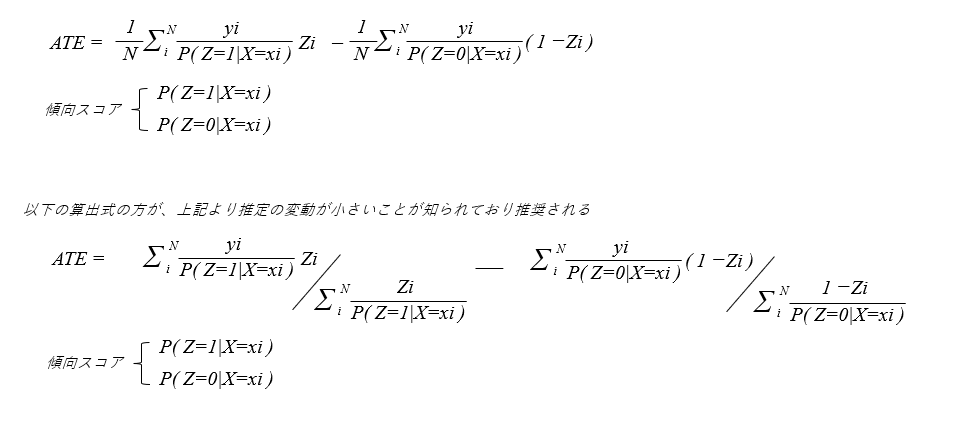
image

N：サンプル数
i：i番のデータ
yi：i番の結果変数
Zi：i番の処置変数
xi：i番の共変量
P(Z=zi|X=xi)：i番の共変量xiにおいて処置変数ziとなる確率＝傾向スコア

DR（Doubly Robust）

  • IPTWの問題を解消した手法
    • IPTW法ではi番目のデータに対し、処置=1と処置=0のどちらかでしかないので、一方しか計算がされない（現実では一方のみしか観測できない）。DR法では観測されない他方（反実仮想の結果変数）を何らかのモデルで推定し、ATEの算式に組み込み推定を行う
    • DRで因果効果を正しく推定するためには「共変量で傾向スコアを正しく推定できている」または「共変量で結果変数を正しく推定できている」のどちらかが必要である
image

Y^0,i：Zi=0のときの結果変数推定値
Y^1,i：Zi=1のときの結果変数推定値

傾向スコア層別解析

  • 傾向スコアを一定のレンジを持っていくつかの層に分け、共変量の影響を除去しようとする方法
    • 傾向スコア0~0.25⇒層a、0.25~0.5⇒層b・・・、0.75~1⇒層dなど
  • 全体に対する層kの重み、層kにおける平均差から、層kの処置効果を推定し、全層分を合計することで平均処置効果を推定する
ATE = 
\sum_{k=1}^{K}\bigl(
(WeightATE_{k})×(ATE_{k})
\bigl)

K：作成した層の合計数
WeightATE_k：層kにおけるATEの重み（層kサンプルサイズ/全サンプルサイズ）
ATE_k：層kにおける平均処置効果

実データを使用して処置効果の推定を行っていく

import pandas as pd
import numpy as np
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
import datetime
import warnings
warnings.simplefilter("ignore")

使用データ

文献要旨

  • 1989年から1994年にかけての米国の5つの病院において、ICUで治療を受けている成人の重症患者5735(人)例を対象とし、重症患者の初期治療におけるRHC（Right Heart Catheterization：右心カテーテル治療）の有効性を検証するために使用された
  • アウトカム：生存時間、医療費、医療強度、ICUと病院での入院期間
  • 傾向スコアを用いた処置の調整後、RHCと特定のアウトカムとの関連を推定するために、ケースマッチングと多変量回帰を使用
  • RHCの傾向スコアに関する多変量回帰のROC面積(AUC)は0.83であり、RHCを行った患者と行わなかった患者の共変量による識別は良好
  • RHCを受けている患者の生存期間が減少しているという結果を示した
生存期間 マッチングなし
生存率差
（NoRHC - RHC）		 マッチングあり
生存率差
（NoRHC - RHC）
30d 7.4% 4.7%
60d 8.3% 5.3%
180d 7.4% 7.3%

前処理

  • 文献で使用されている変数をモデルに採用（欠損の変数は削除）
  • 死亡のカラムがベースなので死亡率・生存率を計算（差分はどちらも同じだが）
  • カテゴリー変数のダミー化
rhc_data = pd.read_csv('rhc.csv')

# 'sadmdte'、'dschdte'、'dthdte'、'lstctdte'をYYYY-MM-dd形式に変換
rhc_data['sadmdte'] = rhc_data['sadmdte'].astype(float)
rhc_data['dschdte'] = rhc_data['dschdte'].astype(float)
rhc_data['dthdte'] = rhc_data['dthdte'].astype(float)
rhc_data['lstctdte'] = rhc_data['lstctdte'].astype(float)
for i in range(len(rhc_data)):
    
    if np.isnan(rhc_data['sadmdte'].loc[i]):
        pass
    else:
        rhc_data['sadmdte'].loc[i] = (datetime.datetime(1899,12,30) + datetime.timedelta(rhc_data['sadmdte'].loc[i])).strftime('%Y/%m/%d %H:%M:%S')
        
    if np.isnan(rhc_data['dschdte'].loc[i]):
        pass
    else:
        rhc_data['dschdte'].loc[i] = (datetime.datetime(1899,12,30) + datetime.timedelta(rhc_data['dschdte'].loc[i])).strftime('%Y/%m/%d %H:%M:%S')
        
    if np.isnan(rhc_data['dthdte'].loc[i]):
        pass
    else:
        rhc_data['dthdte'].loc[i] = (datetime.datetime(1899,12,30) + datetime.timedelta(rhc_data['dthdte'].loc[i])).strftime('%Y/%m/%d %H:%M:%S')
        
    if np.isnan(rhc_data['lstctdte'].loc[i]):
        pass
    else:
        rhc_data['lstctdte'].loc[i] = (datetime.datetime(1899,12,30) + datetime.timedelta(rhc_data['lstctdte'].loc[i])).strftime('%Y/%m/%d %H:%M:%S')

# 死亡日までの日数を計算
for i in range(len(rhc_data)):
    
    try:
        if np.isnan(rhc_data['dthdte'].loc[i]):
            pass
        else:
            pass
        
    except:
            day = (pd.to_datetime(rhc_data['dthdte'].loc[i]) - pd.to_datetime(rhc_data['sadmdte'].loc[i])).days
            rhc_data['days_until_death'].loc[i] = day

# 60日死亡有無、180日死亡有無を追加
rhc_data['dth60'] = 'No'
rhc_data.loc[rhc_data['days_until_death']<=60 ,'dth60'] = 'Yes'

rhc_data['dth180'] = 'No'
rhc_data.loc[rhc_data['days_until_death']<=180 ,'dth180'] = 'Yes'
all_counts_rhc = len(rhc_data[rhc_data['swang1']=='RHC'])
all_counts_norhc = len(rhc_data[rhc_data['swang1']=='No RHC'])

# 死亡率・生存率を計算
## 30日以内の生存率
print('30日内生存率(RHCなし):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='No RHC')&(rhc_data['dth30']=='No')]) / all_counts_norhc,3)))
print('30日内生存率(RHCあり):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='RHC')&(rhc_data['dth30']=='No')]) / all_counts_rhc,3)))
## 30日以内の死亡率
print('30日内死亡率(RHCなし):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='No RHC')&(rhc_data['dth30']=='Yes')]) / all_counts_norhc,3)))
print('30日内死亡率(RHCあり):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='RHC')&(rhc_data['dth30']=='Yes')]) / all_counts_rhc,3)))

## 60日以内の生存率
print('60日内生存率(RHCなし):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='No RHC')&(rhc_data['dth60']=='No')]) / all_counts_norhc,3)))
print('60日内生存率(RHCあり):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='RHC')&(rhc_data['dth60']=='No')]) / all_counts_rhc,3)))
## 60日以内の死亡率
print('60日内死亡率(RHCなし):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='No RHC')&(rhc_data['dth60']=='Yes')]) / all_counts_norhc,3)))
print('60日内死亡率(RHCあり):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='RHC')&(rhc_data['dth60']=='Yes')]) / all_counts_rhc,3)))

## 180日以内の生存率
print('180日内生存率(RHCなし):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='No RHC')&(rhc_data['dth180']=='No')]) / all_counts_norhc,3)))
print('180日内生存率(RHCあり):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='RHC')&(rhc_data['dth180']=='No')]) / all_counts_rhc,3)))
## 180日以内の死亡率
print('180日内死亡率(RHCなし):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='No RHC')&(rhc_data['dth180']=='Yes')]) / all_counts_norhc,3)))
print('180日内死亡率(RHCあり):{}'.format(round(len(rhc_data[(rhc_data['swang1']=='RHC')&(rhc_data['dth180']=='Yes')]) / all_counts_rhc,3)))

# 使用しない変数を削除
# 現時点で不要なカラムを削除（欠損ありも削除）
rhc_data = rhc_data.drop(['cat2','sadmdte','dschdte','dthdte','lstctdte','death','urin1','adld3p','ptid','days_until_death'],axis=1)

# 文献で使用されている変数
columns=['age','sex','race','edu','income','ninsclas','cat1', # cat2は欠損のため除外
'resp', 'card', 'neuro','gastr', 'renal', 'meta', 'hema', 'seps', 'trauma', 'ortho', # 12個とあるが10個しかない
'das2d3pc','ca','surv2md1', # ADL(adld3p)は欠損のため除外
'aps1','scoma1','wtkilo1','temp1', 'meanbp1','resp1','hrt1','pafi1','paco21','ph1','wblc1',
'hema1', 'sod1','pot1','crea1','bili1','alb1', # urin1は欠損のため除外
'cardiohx', 'chfhx', 'dementhx', 'psychhx', 'chrpulhx','renalhx', 'liverhx', 'gibledhx', 'malighx', 'immunhx', 'transhx','amihx',
'swang1', # 処置変数
'dth30','dth60','dth180'] # 13個のcomorbid illnessとあるが12個しかない
rhc_data = rhc_data[columns]

# カテゴリー変数をダミー変数化
category_columns = ['sex','race','income','ninsclas','cat1','resp','card','neuro','gastr','renal','meta','hema','seps','trauma',
                    'ortho','ca','swang1','dth30', 'dth60', 'dth180']
dummy_df = pd.get_dummies(rhc_data[category_columns],dtype=int)
dummy_df = dummy_df.drop(['sex_Female','race_black','income_Under $11k','ninsclas_No insurance','cat1_ARF',
                          'resp_No','card_No','neuro_No','gastr_No','renal_No','meta_No','hema_No','seps_No','trauma_No','ortho_No',
                          'ca_No','swang1_No RHC','dth30_No','dth60_No','dth180_No'],axis=1)
column_data = []
for col in dummy_df.columns:
    col = col.replace('_Yes','')
    col = col.replace('$','')
    column_data.append(col)
    
dummy_df.columns = column_data

# カテゴリー変数化した元のデータを削除
rhc_data = rhc_data.drop(category_columns,axis=1)

# ダミー変数をマージ
rhc_data = pd.concat([rhc_data,dummy_df],axis=1)

# -------------------------------------元データカラム説明-------------------------------------
## 'cat1'：主疾患カテゴリー
## 'cat2'：副疾患カテゴリー
## 'ca'：癌
## 'sadmdte'：研究開始日
## 'dschdte'：退院日
## 'dthdte'：死亡日
## 'lstctdte'：（対象者への）最終接触日
## 'death'：180日以内に死亡
## 'cardiohx'：Acute MI（急性心筋梗塞） Peripheral Vascular Disease（末梢血管障害） Severe Cardiovascular Symptoms (NYHA-Class III)（重症心血管系症状）
##             Very Severe Cardiovascular Symptoms (NYHA-Class IV)（超重症心血管系症状）の有無
## 'chfhx'：うっ血性心不全の有無
## 'dementhx'：Dementia（認知症）　Stroke or Cerebral Infarct（脳卒中）　Parkinson`s Disease（パーキンソン）の有無
## 'psychhx'：Psychiatric History（精神医学的既往歴）　Active Psychosis or Severe Depression（活動性の精神病または重度のうつ病）の有無
## 'chrpulhx'：Chronic Pulmonary Disease（慢性肺疾患）　Severe Pulmonary Disease（重症肺疾患）　Very Severe Pulmonary Disease（超重症肺疾患）の有無
## 'renalhx'：Chronic Renal Disease（慢性腎臓病）　Chronic Hemodialysis or Peritoneal Dialysis（慢性血液透析または腹膜透析）の有無
## 'liverhx'：Cirrhosis（肝硬変）　Hepatic Failure（肝不全）
## 'gibledhx'：上部消化管出血の有無
## 'malighx'：Solid Tumor（固形がん）　Metastatic Disease（転移性疾患）　Chronic Leukemia/Myeloma（慢性白血病/骨髄腫）
##            Acute Leukemia（急性白血病）　Lymphoma（リンパ腫）の有無
## 'immunhx'：Immunosupperssion（免疫不全）　Organ Transplant（臓器移植）　HIV Positivity（HIV陽性）　
##            Diabetes Mellitus Without End Organ Damage（末端臓器障害を伴わない糖尿病）
##            Diabetes Mellitus With End Organ Damage（末端臓器障害を伴う糖尿病）　Connective Tissue Disease（結合組織病）
## 'transhx'：他の病院からの転院（24時間以上）
## 'amihx'：確実な心筋梗塞
## 'age'：年齢
## 'sex'：性別
## 'edu'：教育年数
## 'surv2md1'：2ヶ月生存確率のサポートモデル推定値
## 'das2d3pc'：DASI（デューク活動状態指数）
## 't3d30'：?
## 'dth30'：入院後30日以内に死亡
## 'aps1'：率APACHEスコア
## 'scoma1'：グラスゴー・コーマ・スコア
## 'meanbp1'：平均血圧
## 'wblc1'：白血球数
## 'hrt1'：心拍数
## 'resp1'：呼吸数
## 'temp1'：気温
## 'pafi1'：PaO2/FIO2比
## 'alb1'：アルブミン
## 'hema1'：ヘマトクリット
## 'bili1'：ビリルビン
## 'crea1'：クレアチニン
## 'sod1'：ナトリウム
## 'pot1'：カリウム
## 'paco21'：PaCo2
## 'ph1'：PH
## 'swang1'：右心カテーテル治療（RHC）
## 'wtkilo1'：体重
## 'dnr1'：1日目のDNR状態
## 'ninsclas'：医療保険カテゴリー
## 'resp'：呼吸器診断
## 'card'：循環器診断
## 'neuro'：神経学的診断
## 'gastr'：消化器診断
## 'renal'：腎臓診断
## 'meta'：代謝診断
## 'hema'：血液学的診断
## 'seps'：敗血症診断
## 'trauma'：外傷診断
## 'ortho'：整形外科診断
## 'adld3p'：日常生活動作（ADL）
## 'urin1'：尿量
## 'race'：人種
## 'income'：収入カテゴリー
## 'ptid'：患者ID

RHCなしの場合とありの場合のN日死亡率（生存率）差を集計
⇒概ね文献値と一致

RHCなし RHCあり 差分（NoRHC-RHC）
30d生存率 69.4% 62.0% +7.4%
30d死亡率 30.6% 38.0% -7.4%
60d生存率 62.7% 54.4% +8.3%
60d死亡率 37.3% 45.6% -8.3%
180d生存率 53.5% 46.0% +7.5%
180d死亡率 46.5% 54.0% -7.5%

傾向スコア（処置確率）を算出

# 処置確率の計算
y = rhc_data['swang1_RHC']
X = rhc_data.drop(['dth30','dth60','dth180','swang1_RHC'],axis=1)

# Xに定数項を追加
X_con = sm.add_constant(X)

# モデルの構築
logit_bin_model = sm.Logit(y,X_con)
result = logit_bin_model.fit()

# 処置確率
rhc_prob = pd.DataFrame(result.predict(X_con),columns=['ps'])

# 元のデータに結果をマージ
rhc_data = pd.concat([rhc_data,rhc_prob],axis=1)

ROC-AUCを可視化

# ROC-AUCを算出
value_true = rhc_data['swang1_RHC']
value_score = rhc_data['ps']

plt.figure(figsize=(5,3))
fpr, tpr, thresholds = roc_curve(value_true, value_score)
plt.plot(fpr, tpr)
plt.xlabel('FPR: False positive rate')
plt.ylabel('TPR: True positive rate')
plt.grid()

print('AUC:{}'.format(round(roc_auc_score(value_true, value_score),3)))
image

AUC：0.795
⇒文献ではAUC0.83だったので文献値よりも低くでてしまっている。精度としては高くないが、ROCを見る限りランダムな予測というわけでもない。一定、共変量に基づいた予測はできていそうではあるため、文献値との乖離はあるがこのまま進めることにする。

傾向スコアマッチング/IPTW/層別解析を行う関数を作成

傾向スコアマッチング（非復元）

# 非復元マッチングを行う関数を作成
def ps_matching_without_replacement(data,
                                    outcome,
                                    ps,
                                    treatment,
                                    reference,
                                    target): 
                                    
    # reference:近い値を探す傾向スコアの処置区分（0 or 1）
    # target:近い傾向スコアの探し先の処置区分（0 or 1）

    # D=処置
    D = data[treatment]

    # Y=アウトカム
    Y = data[outcome]

    # Ps=傾向スコア
    Ps = data[ps]

    # D=targetのインデックスと一致する傾向スコアをtarget_listに格納
    target_list = Ps[Ps.index.isin(D[D==target].index)]
    target_copylist = target_list.copy()

    # ATEの初期値を設定
    ATE = 0

    # マッチング回数の初期値を設定
    k = 0

    # マッチング済インデックス
    match_target_list = [] # target（探し先）側

    # 可視化用にreference側もマッチング済インデックスを格納
    match_subject_list = [] # reference（探す値）側

    # D=referenceをベースにインデックスでループ（reference）
    index_list_Drf = D[D==reference].index
    
    # 探す傾向スコアはランダム化する
    random.seed(1234)
    random_index_list_Drf = random.sample(list(index_list_Drf), len(index_list_Drf))
    
    for i in random_index_list_Drf:

        # マッチング済のインデックスはtarget_copylist内のインデックスを参照し傾向スコアを欠損に変換
        for match_idx in match_target_list:
            target_copylist[match_idx] = np.nan

        # インデックスが一致する傾向スコアを取得
        ps_i = Ps[Ps.index.isin(D[D==reference].index)][i]

        # D=targetの傾向スコアからi番目のD=referenceの傾向スコアを差し引き絶対値(abs)を取得。その中で最小の値のインデックス（要素番号）を取得(argmin())しidxに格納
        ## ps_iとtarget_list内の傾向スコアの差の絶対値が一番小さいインデックスを取得＝target_list内で一番近いデータを取得（欠損になっている傾向スコアは除外）
        abs_target_list = np.abs(target_copylist - ps_i)
        idx = abs_target_list[(abs_target_list==abs_target_list.min())&abs_target_list.notna()].index[0]

        # caliperを設定---->0.03
        caliper = 0.03

        # 上記で取得したtarget_list内で一番近いデータ（D=targetの傾向スコア）からps_i（i番目のD=0の傾向スコア）を差し引き、その値が0.03を超えてしまう場合、ループの先頭に戻り以降の処理はなし
        if np.abs(target_copylist.loc[idx] - ps_i) > caliper: # ilocから変更
            continue
        else:
            # キャリパーを超えていない場合、idx番目のD=targetのアウトカムからi番目のD=referenceのアウトカムを差し引く
            ## 算出値をATEに加算
            ATE +=  int(Y.loc[i]) - int(Y.loc[idx])

            # マッチング回数を加算
            k += 1

            # マッチングしたtarget_listのインデックス情報を格納（マッチング済インデックス）
            match_target_list.append(idx)

            # 可視化用に対象群のインデックス情報も格納
            match_subject_list.append(i)

    # 計算回数の平均を算出
    ATE = round(ATE / k,3)

    return ATE

IPTW（推奨パターン）

# IPWを算出する関数を作成
def ipw2(data,
         outcome,
         ps,
         treatment):
    
    Y = data[outcome] # アウトカム
    Ps = data[ps] # 傾向スコア
    trmt = data[treatment] # 処置変数
    
    score_1 = sum(trmt*Y / (Ps)) / sum(trmt / (Ps)) # 処置=1のときのIPWの期待値
    score_0 = sum((1 - trmt)*Y / (1 - Ps)) / sum((1 - trmt)  / (1 - Ps)) # 処置=0のときのIPWの期待値
    score = score_1 - score_0 # 期待値の差分を算出（ATE）
    
    return score

層別解析

# 層別解析（層化解析）を行う関数を作成
def ps_strtfy(data,
              outcome,
              ps,
              treatment,
              step):
              
    # D=処置
    D = data[treatment]

    # Ps=傾向スコア
    Ps = data[ps]

    # Y=アウトカム
    Y = data[outcome]

    # 層ごとのATE格納用に空のリストを設定
    ATE = np.array([])

    # インターバルを設定
    step = step
    interval = np.arange(0,1+step,step)

    for i in range(0,len(interval)-1):

        # idx0・・・D=0(CM視聴なし)であり、i番目のインターバル値 <= Ps < i+1番目のインターバル値に該当するPsのインデックス
        idx0 = Ps[(Ps.index.isin(D[D==0].index)) & (Ps>=interval[i]) & (Ps<interval[i+1])].index

        # idx1・・・D=1(CM視聴あり)であり、i番目のインターバル値 <= Ps < i+1番目のインターバル値に該当するPsのインデックス
        idx1 = Ps[(Ps.index.isin(D[D==1].index)) & (Ps>=interval[i]) & (Ps<interval[i+1])].index

        # インターバルに該当する傾向スコアがない場合は処理を行わない
        if (len(idx0) > 0) & (len(idx1) > 0):

            # 層kのATE重みを算出
            all_sample = len(Ps) # 全症例数
            strt_k_sample = len(idx0) + len(idx1) # 層kの症例数
            strt_k_weight = strt_k_sample / all_sample

            # 層kのATE計算
            ATE_k =  (Y[idx1].mean() - Y[idx0].mean())*strt_k_weight

            ATE = np.append(ATE,ATE_k)

    ATE = round(ATE.sum(),3)
    
    return ATE

30日死亡率を計算していく

傾向スコアマッチング（非復元）

ps_matching_without_replacement(data=rhc_data ,
                                outcome='dth30' ,
                                ps='ps' ,
                                treatment='swang1_RHC' ,
                                reference=1 , # 処置=1（探す値）
                                target=0 ) # 処置=0（探し先）

ATE：0.060（6.0%）

IPTW

ipw2(data=rhc_data ,
    outcome='dth30' ,
    ps='ps' ,
    treatment='swang1_RHC' )

ATE：0.037（3.7%）

層別解析

ps_strtfy(data=rhc_data ,
          outcome='dth30',
          ps='ps' ,
          treatment='swang1_RHC' ,
          step=0.2)

ATE：0.039（3.9%）

結果

（再掲）文献値

生存期間 マッチングなし
生存率差
（NoRHC - RHC）		 マッチングあり
生存率差
（NoRHC - RHC）
30d 7.4% 4.7%

計算結果集計値（30d死亡率）

PS
使用手法		 PS使用なし
死亡率差（＝生存率差）
（RHC-NoRHC）		 PS使用あり
死亡率差（＝生存率差）
（RHC-NoRHC）
マッチング 7.4% 6.0%
IPTW 同上 3.7%
層別解析 同上 3.9%
  • RHCありの患者の方が、なし患者より30日死亡率が高い（＝なし患者の生存率の方が高い）
  • マッチングでは、文献記載の処置効果と上記計算での処置効果にそこそこ乖離があるため、マッチング方法の差異（復元マッチか、キャリパー有無等）や傾向スコア推定モデルの投入変数の差異（欠損している変数を補完等）があると思われる
  • 傾向スコアを使用し共変量の影響を低減させた3つの手法での処置効果はいずれも＜7.4%である

まとめ

  • 傾向スコアを使用したマッチング、IPTW、DR、層別解析を理解
  • 実データを用いた上記手法実装のためのサンプルコードを理解
1
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
1