LoginSignup
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@Takahiro_zzz(Takahiro)

【分析】生存時間分析を学習する

Last updated at Posted at 2024-11-27

目的

  • 過去に生存時間分析の学習を行ったので、その内容を自分用メモとしてまとめる
  • 記事確認いただいた初学者の方が以下の内容を達成できる
    • 生存時間分析への入り口として、実データを通して全容を理解する（興味を持てる程度まで）
    • サンプルコードを通して実装方法を理解する（コピーして使用できる程度まで）

生存分析（生存時間分析）とは

  • 生存時間とは「ある時点から興味のあるイベントが発生するまでの時間のこと」であり、生存分析は疫学に限らず、特定イベントが発生するまでの時間を解析する手法
  • 死亡するまでの時間や病気が再発するまでの時間、機械が故障するまでの時間など、様々なイベント発生にかかる時間やイベント発生確率に対し、解析が可能
  • 最近は中学生の学習範囲に一部あるのか・・・恐ろしい

参考

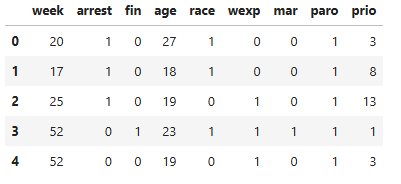
使用するデータ

  • 生存分析用のライブラリ「lifelines」からダウンロード可能なデータセット
  • 1970年に米国メリーランド州の刑務所から釈放され、釈放後に一年間追跡調査された受刑者に関するデータ
  • 釈放された受刑者のうち半数は実験的措置としての財政援助を受け、残りの半数は受けなかった
  • 「week」を生存期間（＝保釈後、再逮捕までの時間）、「arrest」を状態変数（保釈後、再逮捕されたか）とし、その他のカラムは説明変数とする。「fin (財政援助の有無)」や「age (釈放時の年齢)」 といった説明変数が状態変数「arrest」にどのように影響しているか解析していく

カラム名の説明

  • week：釈放後の最初の逮捕までの週数、または打ち切り（生存時間）
  • arrest：逮捕の有無 (1:有)（状態変数）
  • fin：財政援助の有無 (1:有)（共変量）
  • age：釈放時の年齢（共変量）
  • race：人種（1:省略）（共変量）
  • wexp：労働経験の有無 (1:有)（共変量）
  • mar：釈放時の婚姻状況 (1:結婚)（共変量）
  • paro：仮釈放 (1:仮釈放)（共変量）
  • prio：過去の受刑回数（共変量）
# インストール
!pip install lifelines

# ライブラリから使用データセットを読み込み
from lifelines.datasets import load_rossi

rossi = load_rossi()
rossi.head()

【出力結果】
image

生存曲線

  • 横軸に生存期間、縦軸に累積生存率を取り、生存期間におけるイベントの発生状況を視覚的に確認できる
  • 観察期間において、イベントが起きなかったことを「打ち切り」という。カプランマイヤー生存曲線ではこれを計算に含めることができる

（累積生存確率）

S(t_{j}) = \prod_{i | t_i≤t_j}\biggl(
\frac{n_i - d_i}{n_i}
\biggl)

$ti , tj$：時点（$ti ≤ tj$）
$S(tj)$：とある時点までにおける累積生存確率
$ni$：とある時点における生存数（$1$時点前の生存数－$1$時点前のイベント発生数－$1$時点前の打ち切り数）
$di$：とある時点において発生したイベント数

生存曲線の描画

# ライブラリ使用なし：生存確率算出＆生存曲線描画関数
def kmf_plot(data):
    data.reset_index(drop = True,inplace = True)
    gb_data = data[['week','arrest']].groupby('week').agg(['count', 'sum'])
    gb_data.columns = gb_data.columns.droplevel(0)
    gb_data['打ち切り(wi)'] = gb_data['count'] - gb_data['sum']
    gb_data = gb_data.drop('count',axis=1)
    gb_data.reset_index(drop = False,inplace = True)
    gb_data.rename(columns = {'sum':'イベント(di)','week':'経過week(ti)'}, inplace = True)

    allCounts = len(data)
    gb_data['生存数(ni)'] = 0
    for i in range(len(gb_data)):
        if i == 0:
            gb_data['生存数(ni)'].loc[i] = allCounts
        else:
            gb_data['生存数(ni)'].loc[i] = gb_data['生存数(ni)'].loc[i-1] - gb_data['イベント(di)'].loc[i-1] - gb_data['打ち切り(wi)'].loc[i-1]

    gb_data['(ni-di)/ni'] = ( gb_data['生存数(ni)'] - gb_data['イベント(di)'] ) / gb_data['生存数(ni)'] 

    gb_data['生存確率(S(tj))'] = 0
    for i in range(len(gb_data)):
        prob = np.prod(gb_data['(ni-di)/ni'].loc[0:i].values)
        gb_data['生存確率(S(tj))'].loc[i] = prob
        
    # 生存曲線可視化用に「経過week(ti)」「生存確率(S(tj))」のみを取得していく
    tmp = gb_data[['経過week(ti)','生存確率(S(tj))']].copy()
    tmp['add_flg'] = 0
    reshape_tmp = pd.DataFrame()
    
    for i in range(len(tmp)):
        if i < len(tmp)-1:
            base_pb = tmp['生存確率(S(tj))'].loc[i]
            next_pb = tmp['生存確率(S(tj))'].loc[i+1]
            if base_pb != next_pb:
                reshape_tmp =  pd.concat([reshape_tmp, tmp.loc[[i]]],axis=0)
                next_w = tmp['経過week(ti)'].loc[i+1]
                add_data = pd.DataFrame([[next_w, base_pb, 1]],columns=['経過week(ti)', '生存確率(S(tj))', 'add_flg'])
                reshape_tmp =  pd.concat([reshape_tmp,add_data],axis=0)

            else:
                reshape_tmp =  pd.concat([reshape_tmp,tmp.loc[[i]]],axis=0)
        else:
            pass
    
    reshape_tmp.reset_index(drop=True,inplace=True)
    
    # 生存曲線の可視化
    plt.figure(figsize=(10,5))
    plt.plot(reshape_tmp['経過week(ti)'],reshape_tmp['生存確率(S(tj))'])
    plt.title('生存曲線：ライブラリ使用なし')
    plt.xlabel('経過week')
    plt.ylabel('生存確率')
    plt.show()

    # return reshape_tmp コメントアウト

kmf_plot(data = rossi)

【出力結果】
image

イベント発生・打ち切りの識別までは付きませんが、生存率が大きく変動している時点が一目でわかる。
ただ、必死に計算せずとも、ライブラリでさくっと信頼区間まで描画できる

# ライブラリにより生存曲線を描画
from lifelines import KaplanMeierFitter
T = rossi['week'] # TimeのT（時間：生存時間）
E = rossi['arrest'] # EventのE（イベント：再逮捕されたかを表す状態変数）
kmf = KaplanMeierFitter()
kmf.fit(durations = T,
        event_observed = E)

# 信頼区間を含めてプロット
plt.figure(figsize=(5,3))
kmf.plot()
plt.title('生存曲線：ライブラリ使用')
plt.xlabel('経過week')
plt.ylabel('生存確率')

plt.show()

【出力結果】
image

生存曲線の比較

財政援助の有無（fin=0 or 1）によって、イベント発生（再逮捕）までの期間に差異があるのか見ていく

# 財政援助なし
T_fin0 = rossi['week'][rossi['fin']==0]
E_fin0 = rossi['arrest'][rossi['fin']==0]
kmf_fin0 = KaplanMeierFitter()
kmf_fin0.fit(durations = T_fin0, 
        event_observed = E_fin0)

# 財政援助あり
T_fin1 = rossi['week'][rossi['fin']==1]
E_fin1 = rossi['arrest'][rossi['fin']==1]
kmf_fin1 = KaplanMeierFitter()
kmf_fin1.fit(durations = T_fin1,
        event_observed = E_fin1)

# 信頼区間を含めてプロット
plt.figure(figsize=(10,5))
kmf_fin0.plot(color='blue',linestyle='--',label='財政援助なし')
kmf_fin1.plot(color='orange',label='財政援助あり')
plt.title('生存曲線：ライブラリ使用')
plt.xlabel('経過week')
plt.ylabel('生存確率')

plt.show()

【出力結果】
image

【結果の読み取り】

  • 財政援助なしの方が、ありの場合に比べ、イベント発生までの期間（生存期間＝再逮捕までの期間）が短いスパンで繰り返されている、また生存確率が低い。
    ⇒「財政援助：有」の方が再逮捕までの期間が長くなりそうな雰囲気をふわっと感じておく
  • 次項でこの2群の有意差検定を行っていく

比較した2群の生存曲線に有意差があるか

以下2種の検定方法がメジャーのようである。
いずれの検定の場合も検定統計量は自由度1のカイ二乗分布に従う

  • ログランク検定
    • 各時点のイベント数に重み付けしない（どの時点のイベントも平等）
  • 一般化ウィルコクソン検定
    • 各時点のイベント数に重み付け。初期の結果の信頼性が高い場合に用いるよう

$S1(t)$：処置群の生存関数
$S2(t)$：対象群の生存関数

  • 帰無仮説：$S1(t)=S2(t)$
  • 対立仮説：$S1(t)≠S2(t)$

使い分けや検定統計量の算出は以下の記事が参考になりましたので、リンクを貼らせていただきます。

from lifelines.statistics import logrank_test

# ログランク検定
logrank_results = logrank_test(T_fin1, T_fin0,
                               E_fin1, E_fin0)
logrank_results.print_summary()

【出力結果】
image.png

# 一般化ウィルコクソン検定
logrank_results = logrank_test(T_fin1, T_fin0,
                               E_fin1, E_fin0,
                               weightings='wilcoxon')
logrank_results.print_summary()

【出力結果】
image.png

事前設定はしていなかったが有意水準5%として結果を判断するとp≤0.05のため、どちらも帰無仮説を棄却し「処置群と対象群の生存関数には有意な差がある」となる

生存時間に影響を与える要因の探索

Cox比例ハザードモデルは、生存時間に対する重回帰分析にあたる。例えば、とある説明変数が「1」変化したときに、ハザード関数が何倍になるかを算出可能である
以下にはCox比例ハザードモデルを理解するために必要な要素を以下に記載した。

生存関数

死亡時年齢（寿命）で考える。

  • 確率変数$X$が寿命（死亡時年齢）を表し、$f(x)$がその確率密度関数とする（＝とある時点$x$において死亡している確率。$x$は年齢）
  • $F(x)$を$f(x)$のとある時点$x$までの累積分布関数とすると、とある時点$x$までに死亡している確率となる
  • $F(x)$は上記であるため、$1$から引いた$S(x)=1-F(x)$は、とある時点$x$において生存している確率を示す
  • この$S(x)$を生存関数と呼ぶ

ハザード関数

  • ハザードとは：
    時点$t$までは生存しているものの、その直後（次の瞬間）に死んでしまう確率のこと。一般的に言い換えると、時点$t$まではイベント未発生だが、その直後にイベントが発生する確率のこと
  • このハザードを関数として表したものを「ハザード関数($=h(x)$)」と言い、生存関数（$=S(x)$）を用いて以下で表す
h(x)=\frac{f(x)}{1-F(x)}=(-logS(x))'

比例ハザードモデル

  • ハザード関数$h(t)$（$t$は時間）を、共変量$x$（説明変数）の線形結合によって表したもの
  • 以下の式のとおり、ハザード関数は時間$t$に影響されず、$h_{0}$は定数である
  • 比例ハザードモデルにおける時間は、上記のとおり時間$t$に依存せず、生存時間$T$の分布は「指数分布」に限られる、という制約がある
h(t,x) = exp(α+x^{Ｔ}β)=h_{0}\space e^{x^{Ｔ}β}, (h_{0}=exp(α)>0)

⇔h_{0} \space exp(x_{1}β_{1}+x_{2}β_{2}+・・・x_{n}β_{n})

Cox比例ハザードモデル

  • 比例ハザードモデルでは$h_{0}$は定数であったが、ここに時間的変化を取り込み、$h_{0}(t)$としたものを「基準ハザード」という。基準ハザードは$h_{0}(t)=h(x=0,t)$のことであるため、共変量$x$の全てが$0$のときのハザードを意味する
  • Cox比例ハザードモデルでは、比例ハザードモデルとは異なり、生存時間$T$の従う分布に制約が存在しないため、生存時間$T$がどのような分布であっても使用可能なモデルである
  • ハザードに影響を与えそうな変数を見つけ、影響の大きさを測るために用いられる
h(t,x)=h_{0}(t)\space e^{x^{Ｔ}β},(h_{0}(t)>0)

⇔h_{0}(t) \space exp(x_{1}β_{1}+x_{2}β_{2}+・・・x_{n}β_{n})

ハザード比

  • とある$n$個の共変量（説明変数）（$x_{1},x_{2},・・・x_{n}$）のうち、1つの変数が「1」のときのハザードと基準ハザードの比のこと
  • ハザード比が1より大きい場合は、その共変量の上昇がイベントの発生確率上昇に寄与しており、1より小さい場合は、イベントの発生確率減少に寄与することを意味する
  • ハザード比=1.2の場合、その共変量が1単位増加することで、ハザードが1.2倍になることを意味する
    【共変量$x_{2}$のハザード比】
\frac{h(t,x_{2})}{h_{0}(t)} = \frac{h_{0}(t) \space exp(0×β_{1}+1×β_{2}+・・・0×β_{n})}{h_{0}(t)}=exp(β_{2})

比例ハザード性

  • ハザード比が時間経過とともに変化せず一定である性質のこと（＝時間に依存せず、共変量がハザードに与える影響はどの時点においても変わらないということ）
  • Cox比例ハザード回帰ではこの性質を満たすという強い仮定を置いているため、満たさない場合は使用できない
  • Cox比例ハザードモデル使用時には、この性質を満たしているか、検定やプロット（層別log-logプロットで平行性を確認する等）により確認する必要がある

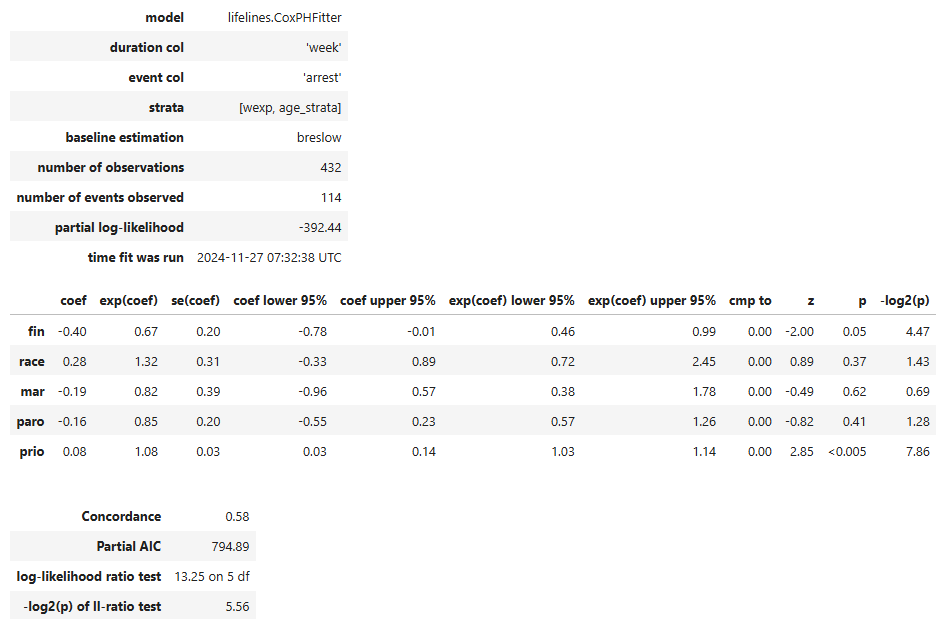
Cox比例ハザード回帰の実行

from lifelines import CoxPHFitter # ライブラリを読み込み

cph = CoxPHFitter()
cph.fit(rossi,
        duration_col='week', # 生存時間 
        event_col='arrest') # 状態変数

cph.print_summary()

【出力結果】
image

【結果の読み取り】
共変量（説明変数）のハザード比（＝ハザードへの影響力）を$exp(coef)$で見てみると、ハザードに影響していそうな変数は以下のとおり（有意水準をp≤0.05として判断すると）

  • 減少に寄与するものとして「fin：財政援助有無」「age：年齢」
  • 上昇に寄与するものとして「prio：過去の受刑回数」

【補足】
推定したモデルを使用して、共変量を変化させた場合の生存曲線を可視化できる（生存曲線のため、縦軸はハザードでなく生存確率）

fig = plt.figure(figsize=(15,5))

ax1 = fig.add_subplot(1,2,1)
cph.plot_partial_effects_on_outcome(covariates='fin', # 変化させる共変量の指定
                                    values=[0, 1], # 上記で設定した共変量のみをvalueの値に変動させる
                                    cmap='coolwarm',
                                    ax = ax1)

ax2 = fig.add_subplot(1,2,2)
cph.plot_partial_effects_on_outcome(covariates='prio', # 変化させる共変量の指定
                                    values=[0, 1, 2, 3, 4], # 上記で設定した共変量のみをvalueの値に変動させる
                                    cmap='coolwarm',
                                    ax = ax2)

ax1.set_title('fin：財政援助有無 exp(β)=0.68')
ax1.set_xlabel('経過week')
ax1.set_ylabel('生存確率')

ax2.set_title('prio：過去の受刑回数 exp(β)=1.1')
ax2.set_xlabel('経過week')
ax2.set_ylabel('生存確率')
plt.show()

【出力結果】
image

推定した生存確率$\hat{P}$とハザード比$exp(β_n)$に関しては以下の関係で計算可能

  • $\hat{P}_i$：1単位増やす前の生存確率
  • $\hat{P}_{i+1}$：1単位増加させたときの生存確率
\hat{P}_{i+1} = \hat{P}_i^{exp(β_n)}

比例ハザード性の検定

  • 帰無仮説：比例ハザード性が成立する
  • 対立仮説：比例ハザード性が成立しない
from lifelines.statistics import proportional_hazard_test

test_results = proportional_hazard_test(cph, rossi, time_transform='rank')
test_results.print_summary(decimals=3, model='untransformed variables')

【出力結果】
image

【結果の読み取り】
有意水準p≤0.05として判断すると、「age：年齢」「wexp：労働経験有無」は比例ハザード性を満たしていない 。

以下ではモデルインスタンスのメソッドを使用して、検定を実施したパターンである。検定におけるアドバイスや「Scaled Schoenfeld residuals（スケール化したショーンフェルド残差）」の対時間プロットを出力できるため便利かも

# cphインスタンスのメソッドで検定を実施する
cph.check_assumptions(rossi, p_value_threshold=0.05, show_plots=True)

【出力結果】

  • 検定結果
image
  • アドバイス
image deeplにかけて翻訳させていただきました笑 - 1. 変数'age'は非比例検定に失敗しました：p値は0.0007です。 - アドバイス1：変数'age'の関数形が正しくないかもしれない。つまり、非線形項が欠落している可能性があります。使用される比例ハザード検定は、不正確な関数形にとても敏感です。関数形の指定方法については、下記のリンク[D]のドキュメントを参照してください。 - アドバイス2: pd.cutを使って変数'age'をビニングし、`.fit`の呼び出しで`strata=['age',...]`で指定してみてください。以下のリンク[B]のドキュメントを参照してください。 - アドバイス3：時間変数との交互作用項を追加してみる。以下のリンク[C]のドキュメントを参照してください。 - 2. 変数'wexp'は非比例検定に失敗しました：p値は0.0063です。 - アドバイス：ユニークな値が少ない（2つだけ）ので、`.fit`の呼び出しに`strata=['wexp', ...]`を含めることができます。下記リンク[E]のドキュメントを参照。
  • Shoenfeld残差プロット
    あまり詳しく理解できていないですが、横軸に時間経過、縦軸がハザード？の残差をたぶん変換したもの？。時間経過によらずその変数の影響が一定であるならば、時間に依存せずまばらな散布図のはず。時間経過とともに何らかの傾向（増加や減少）が見られる場合、その変数の影響が時間経過によって変化している可能性がある・・・。そんな解釈だろうか

【「比例ハザード性が成立する」を棄却しなかった残差プロット（fin：財政援助有無）】
image

【「比例ハザード性が成立する」を棄却した残差プロット（age：年齢、wexp：労働経験有無）】
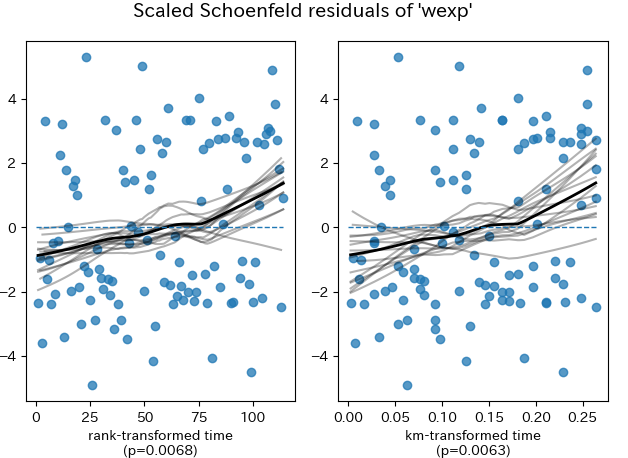
image

image

確かにfinに比べ、ageとwexpは時間経過とともに、残差に増減の傾向がありそうなので、変数の影響が時間経過とともに変化している可能性がありそう

出力されたアドバイスに戻るが、どちらにも「strata=[]の指定」があり、これは「層別Cox比例ハザードモデル」のことである。比例ハザード性を満たさない変数について、その変数でいくつかの層を作成し、その層に従い分けたデータで、それぞれCox比例ハザード回帰を実行する。それにより、比例ハザード性を満たさない変数を除外できる、という方法のようである。
ここでは、「age：年齢」はいくつかの層に分けた新たな変数「age_strata」を作成、「wexp：労働経験有無」は最初から2値のため、そのまま使用することとして、この2つの変数をstrataに指定し、再度Cox比例ハザードモデルを回してみる

# 3歳ごとにカテゴリを付与（公式の記載をそのまま流用）
rossi_strata_age = rossi.copy()
rossi_strata_age['age_strata'] = pd.cut(rossi_strata_age['age'], np.arange(0, 80, 3))
rossi_strata_age = rossi_strata_age.drop('age',axis =1)

# 層別Cox比例ハザードモデルを構築
cph = CoxPHFitter()
cph.fit(rossi_strata_age,
        duration_col='week',
        event_col='arrest',
        strata = ['wexp', 'age_strata']) 

cph.print_summary()

test_results = proportional_hazard_test(cph, rossi_strata_age, time_transform='rank')
test_results.print_summary(decimals=3, model='untransformed variables')

【出力結果】
image

image

【結果の読み取り】

  • 比例ハザード性の仮定が全ての変数で成立している（p≤0.05として判断）
  • 有意な変数は「fin：財政援助有無」「prio：過去の受刑回数」である
  • ハザードに与える影響は
    • fin（財政援助有無）：ありの方がなしに比べ、ハザード関数が0.67倍である（再逮捕の減少要因）
    • prio（過去の受刑回数）：受刑回数が1回増加すると、ハザード関数が1.08倍になる（再逮捕の増加要因）

まとめ

  • 生存分析の入り口となる「カプランマイヤー曲線」、「ログランク検定」、「Cox比例ハザードモデル」に触れた。また、Cox比例ハザードモデルで仮定している「比例ハザード性」、説明変数（共変量）の影響度合い「ハザード比（$exp(β)$）」を実際に確認し、コードを通してそれらの算出方法を理解した
  • 生存分析は「scikit-learn」でも提供があるようなので、興味のある方は是非
  • モデルの予測精度の評価は「Concordance Index」を見ると良さそう（初耳の指標。0~1のレンジで1に近いほど良い）
0
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?