本記事の目的
2クラスの名義尺度を被説明変数とする二項ロジスティック回帰分析のPythonサンプルコードは多く見かけますが、3クラス以上の名義尺度データや順序尺度データを被説明変数とする多項ロジスティック回帰分析はあまり見かけません。本記事では多項ロジスティック回帰分析をPythonのstatsmodelsを使用して実行してみたいと思いますのでサンプルコードの参考になればと思います(結果の解釈には触れてません)。
余談ですが今ならChatGPTでサンプルコードも簡単に出してくれますよ!
サンプルデータ
本記事では疑似的に作成した以下のサンプルデータ(とある病気に関して発症後経過時間、発症時年齢、痛みを生じているか、症状度合い、症状の種別みたいなデータがあったと仮定して)を使用します。
| 発症後経過時間(h) | 発症時年齢 | 疼痛有無※1 | 症状度※2 | 症状種別 |
|---|---|---|---|---|
| 25 | 32 | 1 | 2 | B |
| 8 | 31 | 0 | 0 | B |
| 34 | 33 | 1 | 1 | B |
| 41 | 35 | 1 | 2 | C |
| 8 | 35 | 1 | 2 | B |
| 39 | 29 | 0 | 0 | A |
| 31 | 35 | 1 | 1 | B |
| 32 | 36 | 1 | 2 | B |
| 29 | 30 | 0 | 0 | B |
| 47 | 34 | 1 | 1 | C |
| 35 | 30 | 1 | 2 | A |
| 8 | 33 | 0 | 0 | B |
| 34 | 35 | 1 | 1 | A |
| 41 | 36 | 1 | 2 | C |
| 10 | 35 | 1 | 2 | A |
| 54 | 32 | 0 | 0 | C |
| 31 | 33 | 1 | 1 | B |
| 66 | 34 | 1 | 2 | C |
| 29 | 29 | 0 | 0 | B |
| 47 | 38 | 1 | 1 | A |
※1:0は疼痛なし、1は疼痛あり
※2:0は軽症、1は中等症、2は重症
ライブラリのインポート
本記事では以下のライブラリを使用します。
import pandas as pd
import statsmodels.api as sm
import scipy as sp
from statsmodels.miscmodels.ordinal_model import OrderedModel
二項ロジスティック回帰
こちらは多くの有識者が執筆されてますのでweb検索すれば大量に情報が出てくると思います。
# 説明変数、被説明変数を変数X,yに格納
y = df['疼痛有無']
X = df[['発症後経過時間(h)','発症時年齢']]
# Xに切片を追加
X_con = sm.add_constant(X)
# モデルの構築
logit_bin = sm.Logit(y,X_con)
result = logit_bin.fit()
# 結果を表示
print('----------結果サマリー----------')
display(result.summary())
# オッズ比を算出
print('----------オッズ比----------')
odds_df = pd.DataFrame(result.params,columns=['coef'])
odds_df['odds_ratio'] = sp.exp(odds_df['coef'])
display(round(odds_df,3))
# 平均限界効果を算出
print('----------平均限界効果----------')
display(result.get_margeff().summary())
実行結果
オッズ比と平均限界効果を算出しました。結果の解釈にオッズ比が使用されるケースが多いように思いますが、平均限界効果の方が他者に説明しやすいな、というのが個人的な所感です。この辺の指標について初見の方は以下のリンクがすごくわかりやすいと思います。
https://speakerdeck.com/kanaugust/rozisuteitukuhui-gui-part-2-xi-shu-otuzubi-ping-jun-xian-jie-xiao-guo
多項(名義)ロジスティック回帰
被説明変数が名義尺度であり3クラス以上の場合のロジスティック回帰分析です。二項ロジスティック回帰とほとんど同じように記述するだけです。
こちらもオッズ比、平均限界効果の算出が可能です。
# 説明変数、被説明変数を変数y,Xに格納
y = df['症状種別']
X = df[['発症後経過時間(h)','発症時年齢']]
# Xに切片を追加
X_con = sm.add_constant(X)
# モデルの構築
logit_mn = sm.MNLogit(y,X_con)
result = logit_mn.fit()
# 結果を表示
print('----------結果サマリー----------')
display(result.summary())
# オッズ比を算出
print('----------オッズ比----------')
odds_df =pd.DataFrame(result.params)
odds_df.rename(columns={0:'症状種別B',1:'症状種別C'},inplace=True)
odds_df[['B_odds','C_odds']] = sp.exp(odds_df[['症状種別B','症状種別C']])
display(odds_df)
# 平均限界効果を算出
print('----------平均限界効果----------')
display(result.get_margeff().summary())
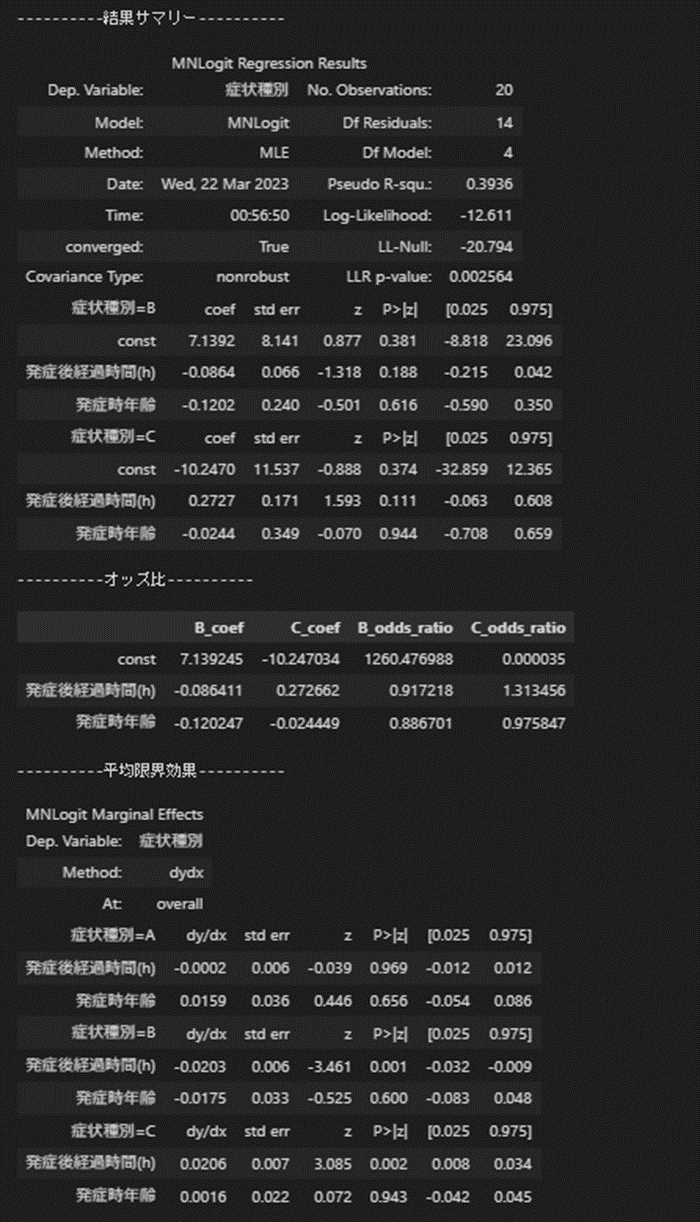
実行結果
特に指定してないですが症状種別Aが参照カテゴリに設定されたようです。
多項(順序)ロジスティック回帰
被説明変数が順序尺度の場合、順序ロジスティック回帰分析を行います。以下の公式ドキュメントを参考に記載してます。
https://www.statsmodels.org/dev/examples/notebooks/generated/ordinal_regression.html
# 説明変数、被説明変数を変数y,Xに格納
y = df['症状度']
X = df[['発症後経過時間(h)','発症時年齢']]
# モデルの構築
logit_od = OrderedModel(y,X,distr='logit')
result = logit_od.fit(method='bfgs',disp=False)
# 結果を表示
print('----------結果サマリー----------')
display(result.summary())
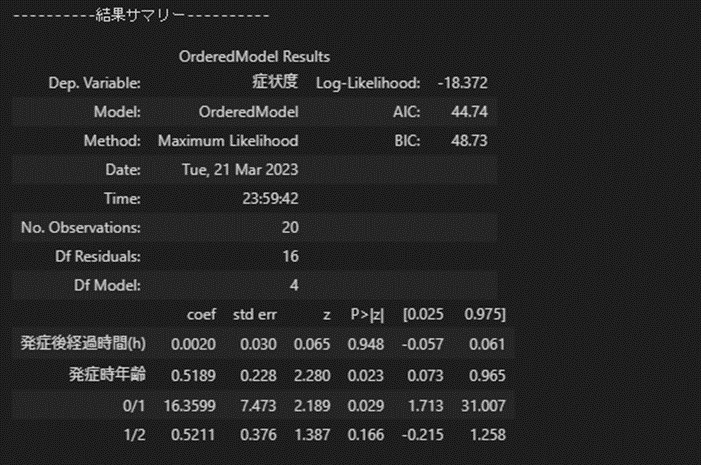
実行結果
上記までのようにオッズ比での解釈は難しいように思います。標準化偏回帰係数を算出して影響の大小を比較するくらいにしか使えないのか、とも思いつつ、もう少し勉強して追記していければと思います。