既に類似のものが存在するかもしれませんが、「検査精度・実際の陽性率・検査対象人口を入力とし、偽陽性・偽陰性の人数とそれらが検査結果に占める割合を計算する」スクリプトを書き、jsFiddle で公開しました。
偽陽性・偽陰性分布計算
https://jsfiddle.net/darutk/Lbhwp1d4/show/
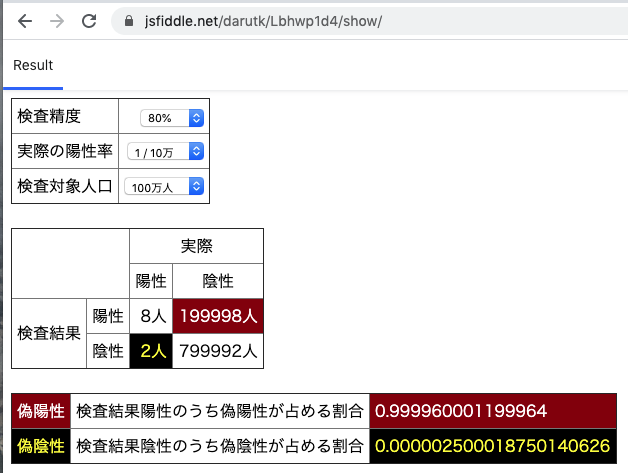
スクリプトの主要な計算部分にコメントをつけると次のようになります。
// 実際の陽性率と検査対象人口から、実際に陽性の人の数を計算する。
let positive_population = Math.round(input.positive_ratio * input.population);
// 実際に陰性の人は、検査対象人口から実際に陽性の人の数を引いたもの。
let negative_population = input.population - positive_population;
//【真陽性】実際に陽性の人のうち、検査結果も陽性になる人の数。
let true_positive = Math.round(input.test_accuracy * positive_population);
//【偽陰性】実際の陽性の人の数から、検査結果も陽性の人の数を引くと、偽陰性の数になる。
let false_negative = positive_population - true_positive;
//【真陰性】実際に陰性の人のうち、検査結果も陰性になる人の数。
let true_negative = Math.round(input.test_accuracy * negative_population);
//【偽陽性】実際の陰性の人の数から、検査結果も陰性の人の数を引くと、偽陽性の数になる。
let false_positive = negative_population - true_negative;
偽陽性の割合は想像以上に高い
**全体に占める実際の感染者の割合が低いと、検査精度が良くても偽陽性になる確率はかなり高くなります。**仮に一万人に一人の割合で感染していたとすると、検査精度が 99% でも、陽性判定のうち実際に陽性なのは 1% くらいです。
対象を絞らずに 1 億人検査すると、999,900 人の偽陽性が出るので、医療崩壊待った無しです。
検査精度の応用
この検査精度の話ですが、意思決定論的なものを学んだことのある人達にはよく知られています。いろいろ応用ができます。
例えば、激しい雨が降る夜に轢き逃げ事件を目撃した人が「車の色は赤だったと思う」と証言したとき、赤い車だけに対象を絞って捜査をすべきでしょうか? もしも、その街に存在する車の中で赤い車の割合が極端に低い場合、むしろ逆に「轢き逃げ事件の車の色は赤ではない」確率のほうが高いでしょう。ですので、車が赤であることの物的証拠がない段階では、見間違いの恐れもある状況下にあった目撃者の証言だけをもとに捜査対象を赤い車だけに絞るのは不適切だと言えます。
おわりに
偽陽性・偽陰性の分布の計算自体は小学生が習う算数でできます。重要なのは、偽陽性・偽陰性の概念を知り、偽判定の割合が直感に反して高くなることを認識しているかどうかです。この概念については、小学校・中学校で教えたほうがよいと昔から思っています。
