Go to Qiita Advent Calendar 2024 Top
LoginSignup
8
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@Takacie

【音声信号処理】FDNリバーブの備忘録

Last updated at Posted at 2021-05-28

どうも、Takacieです。
久々の投稿ですが、今回はVSTの話題からちょっとだけ逸れて、音声信号処理の備忘録を書きます。

経緯

趣味でリバーブのVSTプラグインを作っていて、Manfred R. Schroeder(名前の読みはシュローダーが正しい？)氏が考案したアルゴリズムをこちらのサイトを見ながら実装していたのですが、どうも残響音のメタリック感が気になり始めました。色々調べていると、かの有名なValhalla RoomでおなじみValhallaのSean Costello氏が「シュローダー式はアカン(要約)」と言っているのを見てアルゴリズムを変えたいなーと思い更に調べたところ、FDN(Feedback Delay Networks)という方式があるのを知り、理解が難しそうだったので備忘録として残そうと考えました。
日本語の情報が少なく、個人的な解釈が多々あるので、間違っていれば有識者の方はどうかご指摘ください。

1. FDNリバーブレーション概要

FDNのブロック図は以下のようになっています。
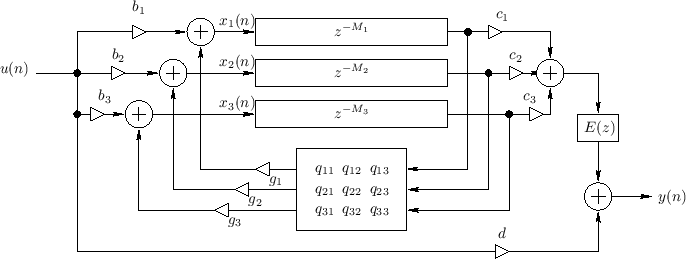
fdn_block_diagram.png
まず、$z^{-M_{i}}$はディレイラインで、$M_{i}$はその遅延サンプル数です。
$b_{i}$と$c_{i}$は残響音のインプット、アウトプットにかけるゲインです。これは設計者が決めるようですが、自分は$b_{i}=1, c_{i}=1/ディレイラインの本数$としました。
$q_{11}$~$q_{33}$が囲まれている四角は次のセクションで説明するフィードバック行列となります。
$g_{i}$はフィードバック行列を計算した後にかけるゲインです。これは残響音の減衰量を決めます。これをLPFに置き換えて、現実世界の空間で起こる高周波減衰を再現したりもします（後述）。
$E(z)$は$g_{i}$をLPFに置き換えた場合に生じる微妙な歪み(coloration)を補正するために用いるフィルタです。
$d$はオリジナル音源成分にかけるゲインです（一般的に$d \leq 1.0$、dはdryの略？）。

2. ロスレスなフィードバック行列の選択

残響音のインパルス応答は、指数関数的に減衰するノイズに似ているのが理想なので、リバーブを設計する際は、残響時間を無限にすることから始め、リバーブを良い "ノイズジェネレータ" にすることを意識する（インパルス応答が周波数的に平たいノイズになるようにする）と良いらしいです。
FDNリバーブでは、上記のインパルス応答によって生成される「(知覚的な)ホワイトノイズ」の周波数的な平たさは、FDNのフィードバック行列の選択と、FDN内のディレイラインの長さに強く影響されます。ここでロスレスなフィードバック行列を選択することで、周波数的に偏りのないノイズが生成されます。よく知られているロスレスなフィードバック行列の選択には次のようなものがあります。

2.1. アダマール行列（Hadamard Matrix）

アダマール行列は以下の式から得られる行列です。

H_{1} = 
\begin{bmatrix}
1
\end{bmatrix}

H_{2^k} = \frac{1}{\sqrt{2}}
\begin{bmatrix}
H_{2^{k-1}} & H_{2^{k-1}} \\
H_{2^{k-1}} & -H_{2^{k-1}}
\end{bmatrix}
\quad(1 \leq k \in N)

例として、$H_{2}$と$H_{4}$の場合を挙げると、

H_{2} = \frac{1}{\sqrt{2}}
\begin{bmatrix}
H_{2^{0}} & H_{2^{0}} \\
H_{2^{0}} & -H_{2^{0}}
\end{bmatrix}
= \frac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}

H_{4} = \frac{1}{\sqrt{2}}
\begin{bmatrix}
H_{2^{1}} & H_{2^{1}} \\
H_{2^{1}} & -H_{2^{1}}
\end{bmatrix}
= \frac{1}{2}
\begin{bmatrix}
1 & 1 & 1 & 1 \\
1 & -1 & 1 & -1 \\
1 & 1 & -1 & -1 \\
1 & -1 & -1 & 1
\end{bmatrix}

となります。

2.2. ハウスホルダーフィードバック行列（Householder Feedback Matrix）

ハウスホルダーフィードバック行列は以下の式から得られる行列です。

A_{N} = I_{N} - \frac{2}{N}U_{N}

ここで、$I_{N}$は$N \times N$の単位行列で、$U_{N}$は$N \times N$の全ての要素が$1$の行列です。
例として、$A_{4}$の場合を挙げると、

A_{N} = 
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
- \frac{1}{2}
\begin{bmatrix}
1 & 1 & 1 & 1 \\
1 & 1 & 1 & 1 \\
1 & 1 & 1 & 1 \\
1 & 1 & 1 & 1
\end{bmatrix}
=
\frac{1}{2}
\begin{bmatrix}
1 & -1 & -1 & -1 \\
-1 & 1 & -1 & -1 \\
-1 & -1 & 1 & -1 \\
-1 & -1 & -1 & 1
\end{bmatrix}

となります。
この行列は、元々$N$が$2$の累乗の場合に少ない計算量で処理できますが、特に$N=4$の場合に優れており、さらに計算量が少なく済むようです。
また、$N$が$4$より大きくなると、対角線と非対角線のバランスが崩れて良い結果が得られなくなってしまうため、例えば$N=16$にしたい場合には、

A_{16} = 
\begin{bmatrix}
A_{4} & -A_{4} & -A_{4} & -A_{4} \\
-A_{4} & A_{4} & -A_{4} & -A_{4} \\
-A_{4} & -A_{4} & A_{4} & -A_{4} \\
-A_{4} & -A_{4} & -A_{4} & A_{4}
\end{bmatrix}

のようにする方法が提案されています。（それだけ$A_{4}$のバランスが良いらしい）
※所々曖昧な表現ですが、詳しくは参考元にて。

2.3. ユニタリ行列（Unitary Matrix）

ユニタリ行列とはある正方行列$A$の転置行列$A^{T}$と$A$の逆行列$A^{-1}$が等しくなるような正方行列$A$です。実際はユニタリ行列は複素行列で、実数に限定されたものを直交行列と呼ぶようですが、参考元がユニタリ行列と記述しているのでそのままにしておきます。

A^{T} = A^{-1}

3. 遅延サンプル数の選択

FDNのディレイラインの長さ（ブロック図で言う$M_{i}$で、遅延されるサンプル数で表される）は、通常、互いに素となるように選択します。そうすることにより、周波数的に偏りのないノイズが生成され、結果的に残響音の質が向上します。この指標を "モード密度" と呼び、これが低いとリンギングが発生したり、不均一な振幅変調になる恐れがあります。

3.1. モード密度の要件

モード密度の単位は$[サンプル数/Hz]$で表されます。先程モード密度が低い場合の悪影響について言及しましたが、高すぎても良くない（？）ようで、残響時間が$1$秒の場合のモード密度は$0.15$程度が適切だと言われています。
これを踏まえて、十分なモード密度を得るには、$M := \sum_{i=1}^{N} M_{i}$（全てのディレイラインの遅延サンプル数の和）として、

M \geq 0.15t_{60}f_{s}

を満たす必要があります。
ここで、$t_{60}$は残響時間$[s]$で、$f_{s}$はサンプルレートです。
例として、サンプルレートが$48.0[kHz]$、残響時間が$2[s]$の場合は$M \geq 0.15248,000 = 14,400$となります。

個人的に、$\bar{M} = M / N$として、

\bar{M} \geq \frac{0.15t_{60}f_{s}}{N}

とすると、平均的にどのくらいのディレイラインの長さが必要なのかが分かって扱いやすかったです。
例えば、上の例の条件でディレイラインの本数$N = 4$とすると、$\bar{M} \geq 3600$となるので、実装時には最大サイズが$3600$以上のバッファ（ディレイライン）が4本必要になるなーといった具合です。

3.2. 平均自由行程

上記のモード密度とともに、ディレイラインの長さの目安になるのが理想の残響空間における平均自由行程です。
平均自由行程とは、音の波が障害物にぶつかって反射するまでの平均的な距離と定義されています。平均自由行程の近似値$\bar{d}$は次の式で表されます。

\bar{d} = 4 \frac{V}{S}

ここで、$V$は残響空間の体積$[m^{3}]$、$S$は残響空間の総表面積$[m^{2}]$1です。

\frac{\bar{d}}{cT} = \frac{1}{N} \sum_{i=1}^{N} M_{i}

ここで、$c$は音速2、$T$はサンプリング周期（サンプルレート$f_{s}$を用いて$T = 1/f_{s}$としても良い）、$N$はディレイラインの数を表しています。また、右辺は前述の$\bar{M}$と等しいので、十分なモード密度の条件と合わせて変形していくと、

\frac{\bar{d}}{cT} \geq \frac{0.15t_{60}f_{s}}{N}

t_{60} \leq \frac{\bar{d}N}{0.15 c}

3.3. 遅延サンプル数の具体的な決め方

実を言うと、こちらのサイトに書いてあるように、各ディレイラインの遅延サンプル数の決め方は試行錯誤によるところが大きいです。
信号処理言語Faustのライブラリでは、動的に残響時間を変化させるために、少ない計算量で各ディレイラインの遅延サンプル数を決める関数が実装されています（解説と実装(prime_power_delays関数)）。しかし、自分で実装してみたところ、確かに計算量は少なく済むようですが、自分が望んでる遅延サンプル数とは程遠い値になったりもします。
また、「そもそもシュローダー式と構造が違うんだから、互いに素じゃなくても適切な遅延サンプル数を決められるのではないか？」というように結論づけている論文もあるので、ここはまだまだ改善の余地があると思います。

ということでちょっと考えてみた

個人的には、計算量云々よりも、動的に残響時間を変化させていく中で、できるだけ自分の望んだ遅延サンプル数（とその間隔）を維持したいなと思い、なんとなく自分で良さげなアルゴリズムを考えてみました。
イメージとしては、まず素数のテーブルと、各ディレイラインの遅延サンプル数が素数テーブル上で基準から何インデックス分離れているかの配列を予め作っておきます。
残響時間を設定するタイミングで適切なモード密度から基準となる遅延サンプル数を決め、それに一番近い素数のインデックスを保持すると、各ディレイラインの遅延サンプル数は素数テーブル上の一定間隔のインデックスによる素数に定まることになります。（説明が難しい）
重要な箇所を抜選したコードを置いておきます。

重要なコードを断片的に抜選(c++)
// まず、max_numまでの素数をズラッと並べたテーブルを作成する。
std::vector<int> primes;
void generatePrimes(int max_num);

// 基準遅延サンプル数とそれに一番近い素数のインデックス。後述のsetReverbTime()で決まる。
int basis_sample_;
int basis_index_;

// 基準遅延ミリ秒数からどれだけ離れているか[ms]
float offsets_ms[16] = { 0.0f, -1.5f, 1.7f, -2.9f, 3.1f, -4.3f, 4.8f,  -6.0f,
                         6.2f, -7.4f, 7.9f, -8.9f, 9.4f, -9.6f, 10.3f, 11.4f };

// これはエクセルで素数とインデックスのグラフを作ってその近似式を関数化したもの。近似された素数テーブルのインデックスが返される。
// 平均で7インデックス程度の誤差はあるが、大体50サンプル(fs=44,100で1msの誤差)なのでまあ許容範囲。
int approPrimeIndex(float x) { return -6346 + 1.1547f * std::sqrt(1250 * x + 3.05982f * 10000000); }

// offsets_msとサンプルレートより、基準から何インデックス分離れているか計算する。
int offsets_index[16];
for (int i = 0; i < num_delayline; i++) {
  offsets_index[i] = approPrimeIndex(basis_sample_ + (samplerate / 1000.0f) * offsets_ms[i]) - basis_index_;
}

// 残響時間設定時に基準となる遅延サンプル数を設定する関数。
void setReverbTime(float new_value) {
  reverb_time_ = new_value;
  // さっきの扱いやすい式変形のMバーを基準とする
  int modal_density_samples = (0.15f * new_value * samplerate_) / num_delayline_;
  basis_index_ = approPrimeIndex(modal_density_samples);
  basis_sample_ = primes_[basis_index_];
}

// i番目のディレイラインの遅延サンプル数を入手したい場合はこう。
primes_[basis_index_ + offsets_index[i]];

この方法を使って実装したFDNの動画です。ディレイライン数は$16$として、フィードバック行列にはアダマール行列を使用しています。

残響時間を変えるときにブチブチノイズが鳴らないから、多分計算量も少なく済んでると思う...。あと、ツイートの通り、FDN単体で低コストな良いリバーブを作るのは正直厳しいです。ディレイラインの本数が4本くらいのFDNにシュローダー式リバーブで使われているコムフィルタやオールバスフィルタを組み合わせたりすると良いんじゃないかなーと思います。

4. 任意の残響時間にするために

上記までの説明だけでは、残響時間は無限のままですので、任意の残響時間を設定できるようにします。これには方法が２種類あり、ブロック図の$g_{i}$を計算する方法と、$g_{i}$をローパスフィルタに置き換える方法があります。後者は現実世界の空間で起こる高周波減衰を再現できますが、また実装が複雑になってきます。

4.1. ゲインgを計算する方法

まず、リバーブの残響時間は「音のエネルギーが$-60dB$減少するまでの時間」と定義されています。そのためには、あるサンプルがフィードバックされる度にゲイン$g$をかけることで、信号が$0.001$倍になるようにします。
ちなみに、何故$0.001$倍なのかというと、音圧の倍率とデシベル$n$が次の関係にあるためです。

音圧の倍率 = 10^{\frac{n}{20}}

よって、ゲイン$g$は以下の式で表されます（おそらく、ブロック図中の$g_{i}$は全て同じ値で良いと思います）。一番右の式は真ん中の式を近似したものです。

g = e^{-3ln(10)/t_{60}f_{s}} \approx 1 - \frac{6.91}{t_{60}f_{s}}

実際、ある信号の大きさ$x$は$t_{60}f_{s}$回のフィードバックの後に$0.001x$となっていれば良いはずです。
信号が$t_{60}f_{s}$回フィードバックされるごとに乗算されていくので、

x (e^{-3ln(10)/t_{60}f_{s}})^{t_{60}f_{s}} = xe^{-3ln(10)} = 0.001x

となり条件を満たしています。

4.2. ゲインgをLPFに置き換える方法

（私の知識不足により準備中＆勉強中）

4.3. 微妙な歪み(coloration)の補正フィルタ$E(z)$

ゲインgをLPFに置き換えた場合に生じる微妙な歪み(coloration)は、ブロック図中では$E(z)$で表されているフィルターにより補正することができる。
（私の知識不足により準備中＆勉強中）

#参考
[1]株式会社ARI, "リバーブ、残響効果", http://www.ari-co.co.jp/service/soft/reverb-1.htm
[2]Julius O. Smith III, "Physical Audio Signal Processing", "FDN Reverbration", 2010, https://ccrma.stanford.edu/~jos/pasp/FDN_Reverberation.html
※[2]はDSP Relatedにて１ページにまとめられています
[3]Fritz Menzer, Choosing Optimal Delays for Feedback Delay Networks, 2014, http://pub.dega-akustik.de/DAGA_2014/data/articles/000025.pdf

  1. 壁四面・天井・床の面積の合計。窓やドアがある想定ならその面積は引く
    この値をディレインラインの長さと紐付けるには、各ディレイラインの長さを平均自由行程の遅延と見なして、次のようにします。 ↩

  2. 一般的には$340[m/s]$とか$343[m/s]$
    という不等式が導けます。これをどう使うのかというと、例えば、奥行き$44[m]$、幅$20[m]$、高さ$16[m]$のコンサートホールのような空間を想定しているとして、平均自由行程を求めると$\bar{d} = 14.79$となります。ディレイラインの本数を$N = 16$とすると、上記の不等式は、$t_{60} \leq 4.60$となり、この空間を想定した場合、十分なモード密度を維持するためには残響時間を$4.60[s]$以下に収めないといけないということになります。
    つまりディレイラインの長さを決める際には、少なくとも残響時間から決める方法と、ある特定の空間を想定する方法が考えられます。なお、ディレイラインの長さを動的に変更する実装にするなら、特定のモード密度を維持したまま残響時間を自由に変えたりすることもできると思います。 ↩

8
6
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?