組み合わせnCrの数値計算

#はじめに

組み合わせ$nCr$の計算を手でやるのが面倒なのでPCでやろうと思いましたが，意外と簡単に行かないことがわかりました．組み合わせの数（コンビネーション）を求めるプログラミングについてまとめてみました．
単純に考えれば
$$nCr=\frac{n!}{r!(n-r)!}$$
なので例えば重複のないボールが$5$個ある状態から$3$個取り出す組み合わせは
$$\frac{5\cdot4\cdot3\cdot2\cdot1}{3\cdot2\cdot1\times2\cdot1} = \frac{120}{6\times2}$$
で簡単だなーと思いながら$n$を増やしていくとかなり危険で，例えば$n$=13だと
$$ _{13}C _{5}=\frac{13\cdot12\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}{5\cdot4\cdot3\cdot2\cdot1\times8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1} = \frac{6,227,020,800}{120\times40320} = 1287$$
となります．
C言語のintは最大値が$$2,147,483,647$$なのでゆうに$n\geq13$でオーバーフローします．
試してみます．

#include <stdio.h>

int main(void){
  int i;
  int ans = 1;
  for(i=1; i<=13 ; i++){
    ans *= i;
    printf("%d (n=%d)\n",ans,i);
  }
}

で

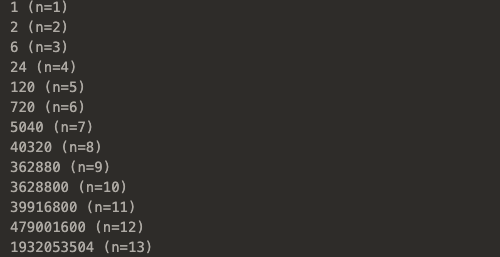
このようになります．13の階乗に関しては
$$13! = 6,227,020,800 $$ $$= 1,932,053,504 + 2\times2,147,483,647 $$ $$\equiv 1,932,053,504\quad(mod\quad4,294,967,296)$$
なので，きちんと（？）オーバーフローしています．ちなみに，modが4294967295なのは，intが-2147483648 ～ 2147483647の合計4294967295個の値をとりうるのでこのようにしました．
例えば2147483648は1つ分だけオーバーフローしてしまうためにintでは-2147483648と表示されます．これは，二進数の一番左側の数字が1の時をマイナスとして処理するためです．
long longでも最大値は$$9,223,372,036,854,775,807 \sim 9\times 10^{18}$$で，$$21!\sim5\times 10^{19}$$から$n\geq21$でオーバーフローします．（ちなみにこの階乗の計算は手元の関数電卓を叩いて計算しています．）
メモリ指定すればいくらでも計算できる気がしますが，組み合わせ$nCr$に関してはもっと効率よく計算するアルゴリズムがあるようです．

計算の考え方

パターン1

コンビネーション
$$nCr=\frac{n!}{r!(n-r)!}$$
を$r$に関しての漸化式を用いて表現することができれば，$n!$などを計算することなく組み合わせを求めることができます．
実際，異なる$n$個のものから$r$個取り出す組み合わせの数$_nC_r$と異なる$n$個のものから$r-1$個取り出す組み合わせの数$ _nC _{r-1}$の関係を無理やり考えるためにその比を解析的に計算してみると
$$\frac{_nC_r}{_nC _{r-1}}=\frac{\frac{n!}{r!(n-r)!}}{\frac{n!}{(r-1)!(n-r+1)!}}=\frac{(r-1)!(n-r+1)!}{r!(n-r)!}=\frac{(r-1)!(n-r+1)\cdot(n-r)!}{r\cdot(r-1)!(n-r)!}=\frac{n-r+1}{r}$$
なので
$$_nC_r=\frac{n-r+1}{r} {}_nC _{r-1}$$
という漸化式が求められます．
この漸化式は階乗などが現れないのでオーバーフローを気にせずに数値計算できます．←ここが重要
ちなみに漸化式を数値的に解くには初期値が必要ですが，これは
$${}_n{C}_0 =\frac{n!}{0!n!}= 1\quad\left(0!=1\right)$$
を考えるとで定義できます．つまりこの漸化式は$n\geq0$で定義されたものでであることに気をつけましょう．
また${}_n{C}_0$はn個の物を0個選ぶ組み合わせで，言い換えれば何も選ばないという一通りしか考えられないので${}_n{C}_0=1$となるのは自然な考え方です．
（この記事では組み合わせの数の解として$nCr$を考えているのでそもそもn=-1などは考えていないということです．）

パターン2

上記以外でも漸化式を考えることができます．
パスカルの三角形は以下のようになっています

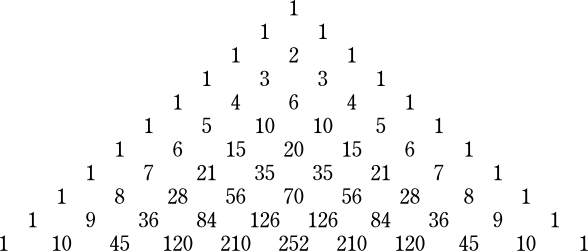
これは二項定理における$(a+b)^n$の各項の係数がパスカルの三角形の上からn段目に対応しているわけですが，このことから
$$ {}_n{C}_r = {} _{n-1}{C} _{r-1} +{} _{n-1}{C} _{r} $$
と予想されます．
実際に計算していくと

 {} _{n-1}{C} _{r-1} +{} _{n-1}{C} _{r} = \frac{(n-1)!}{(r-1)!\left((n-1)-(r-1) \right)!} + \frac{(n-1)!}{r!\left((n-1)-r \right)!} \\ 
= \frac{(n-1)!}{(r-1)!\left((n-1)-r \right)!}\left(\frac{1}{n-r}+\frac{1}{r}\right)\\ 
=\frac{(n-1)!}{(r-1)!\left(n-r-1 \right)!}\left(\frac{n}{r(n-r)}\right)\\
=\frac{n!}{r!(n-r)!}=nCr 

このように計算でき，確かにこの漸化式が成り立っていることがわかります．この漸化式を用いると後述の再帰を用いたものが考えられます．

コードの実装

以上のことから，コンビネーションが漸化式によって表現することができました．
やはりアルゴリズムを考えているのでC言語を用いて実装します．
正直なところPython3などはメモリの許す限り数値を格納できるので，恩恵が感じにくいです．（が，高速化はされるはずです）
漸化式なので（プログラミング初心者が）わかりやすいループを使う方法（パターン１）と，わかれば直感的にとらえやすい再帰関数を使う方法（パターン２）があります．ここでは両方実装してみます．

ループを用いたコンビネーションの数値計算（パターン１）

ループ表現では，漸化式が
$$ {}_n{C}_r = \frac{n-r+1}{r}\cdot\frac{n-(r-1)+1}{r-1}\cdots\frac{n-3+1}{3}\cdot\frac{n-2+1}{2}\cdot\frac{n-1+1}{1}\cdot 1$$
になるのでこれをforループを使って実装します．上の式における一番右の因子を順にかけていきます．

#include <stdio.h>

int main(void){
  int i,n,r;

  printf("Enter number of n:");scanf("%d",&n);
  printf("Enter number of r:");scanf("%d",&r);
  long nCr=1;
  for(i=1;i<=r;i++){
    nCr = nCr*(n-i+1)/i;
  }
  printf("%dC%d=%ld\n",n,r,nCr);
  return 0;
}

結果

例えば ${}_{13}{C}_5$は上で見たように$13!$がオーバーフローするので愚直に計算するようなコードではバグが生じるので，これを計算させます.

1287通りと計算してくれました．ありがたい．

再帰をもちいたコンビネーションの数値計算（パターン２）

素人なのでループを使った処理と再起を使った処理ではどちらの方がメモリ消費量が少ないのかは知りませんが，個人的には再帰でやった方がコンピュータが計算してくれる感が強くて好きです．漸化式は
$$ {}_n{C}_r = {} _{n-1}{C} _{r-1} +{} _{n-1}{C} _{r} $$
を考えれば，
$${} _{n-1}{C} _{r-1}={} _{n-2}{C} _{r-2} +{} _{n-2}{C} _{r-1}$$
$${} _{n-1}{C} _{r}={} _{n-2}{C} _{r-1} +{} _{n-2}{C} _{r}$$
というようにどんどん代入していくことができます．どんどん代入していけばいつかは
$${}_i{C}_i\quad(1\leq i \leq r)$$
もしくは
$${}_j{C}_0\quad(1\leq j \leq n)$$
のいずれかになり，
$${}_i{C}_i =1,{}_j{C}_0 =1$$
が恒等的に成り立つのでこれを再帰の出口に設定します．

#include <stdio.h>
int combination(int n, int r){
  if ( r==0 || r==n ){
    return 1;
  }else{
    return combination(n-1,r-1)+combination(n-1,r);
  }
}
int main(void){
  int i,n,r;
  printf("Enter number of n:");scanf("%d",&n);
  printf("Enter number of r:");scanf("%d",&r);
  long nCr=combination(n,r);
  printf("%dC%d=%ld\n",n,r,nCr);
  return 0;
}

結果

同様にn=13,r=5でお願いしました．

一致してます！
ということでここまでにしようと思います．

#　おわりに
意外とコンビネーションでもめんどくさいです．
他にも再帰とループでどっちの方が処理が速いのかなど気になるところはありますが，そこまでの最適化を考える必要があるのかわからないのと疲れたのでここまでにします．