#はじめに
この記事では様々な一変数関数の形を出力して表示してみています。
式の形を眺める面白さなどを感じていただければ幸いです。また数学には疎いため、関数の名前はほとんど知りません。
xの定義域に関しても式の対称性などは気にしているつもりですが、直感的に定義しています。
pythonを使って計算しています。
## 計算方法
計算方法は以下のコードです。
import numpy as np
from matplotlib import pyplot as plt
def xRange(start,end,rate=1000):
r = (end-start)/rate
return np.arange(start,end+r,r)
def func(x):
return #出力したい関数
def yRange(y,rate=10):
min = np.min(y)
max = np.max(y)
delta = (max - min)/rate
return min - delta,max + delta
def main():
x = xRange(-10,10)
y = func(x)
plt.plot(x,y)
plt.ylim(yRange(y))
plt.ylabel("Function")
plt.xlabel("Arguments")
plt.show()
if __name__ == '__main__':
main()
##関数
-
シグモイド関数 $$ f(x) = \frac{1}{1+exp(-x)} $$
xの係数を逆にする $$ f(x) = \frac{1}{1+exp(x)} $$
-
標準正規分布 $$ f(x) = \frac{1}{\sqrt{2\pi}} exp\biggl(-\frac{x^{2}}{2}\biggr) $$
x^2の係数を逆にする $$ f(x) = \frac{1}{\sqrt{2\pi}}exp\biggl(\frac{x^{2}}{2}\biggr)$$
誤った考察
~~非対称なのが気になります。0に対して対称な定義域[-10,10]で描画も偶数個の点で均等にしているので、自分の知識ではなぜ非対称に描画されるのかわかりませんでした。pyplotの問題かもしれません。~~考察
コメントでご指摘いただきました。ありがとうございます。 上記のxRangeの定義では中心点を考慮していないために xRange(-10,10)[-1] の値が9.979999999999574となっていました。 xRangeを中心点で対称になるように定義するのがベストなのかもしれませんが、とりあえず原点を考慮したxRangeのreturnを return np.arange(start,end,r) から return np.arange(start,end+r,r) と更新しました。 以下、更新前のグラフ -
関数名[?] $$ f(x) =\frac{1}{e^{-x}+e^{x}} $$
-
関数名[?] $$ f(x) = e^{-x}+e^{x} $$
備考
xRangeを更新しました。 以下、更新前のグラフ -関数名[?] $$ f(x)=\frac{1}{log(x)} $$
考察
$$ log(1) = 0 $$なので$$ x=1 $$が特異点となっています。 $$x \rightarrow 1-0 \Rightarrow \frac{1}{log(x)} \rightarrow -\infty $$ $$x \rightarrow 1+0 \Rightarrow \frac{1}{log(x)} \rightarrow \infty $$ の非連続関数です。- 関数名[?] $$ f(x)=\frac{exp(x)}{log(x)} $$
間違った計算
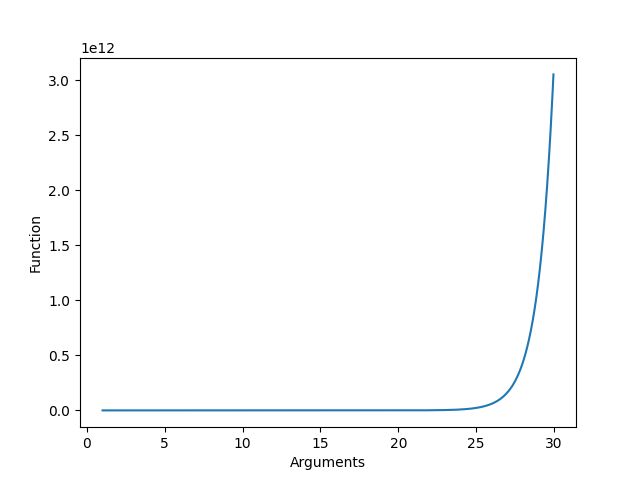 ~~あまり面白くない感じがしますが、logの0度合いがexpの∞具合に負けるのが[25,30]近辺だということです。（ほんまか？)~~
[追記]
全然考察がなっていませんでした、すみません。上記のコード場合xのスケールによってrate(xの離散幅)が変わってしまうため、無限大の処理が荒すぎることからx->1+0の近辺の計算がうまくできていませんでした。
- 関数名[?] $$ x\log{x^2} $$
-関数名[?] $$ x^3\log{x^2} $$
関数名[?] $$ \log{\frac{1}{x^2}} $$
#最後に
初めての投稿なのでかなり至らぬ点があると存じます。随時更新予定です。