量子力学 自由粒子の確率密度分布の時間発展をプロットしてみた

はじめに

量子力学を考える上で、粒子の波動関数を考えることは非常に重要なテーマです。ここではプロパゲータを用いた波動関数の表現から波動関数を考えていきます。
今回は波動関数が
・ガウス分布（正規分布）の初期状態（一次元調和振動子の基底状態など）
・ハミルトニアンがある時刻$ t_0 $で自由粒子になった場合
の確率密度分布の時間発展をプロットしてみます。（一次元）

具体的な条件式

初期状態
$$ \Psi(t_0,x)= \left( \frac{1}{\sqrt{\pi} \Delta} \right)^\frac{1}{2} \exp \left[-\frac{x^2}{2\Delta^2} \right] $$
$$ (分散:\Delta^2) $$
ハミルトニアン
$$ \hat{H} = \frac{\hat{P}^2}{2m} $$
積分核
$$ \left(\frac{m}{2\pi i\hbar T}\right)^\frac{1}{2} \exp \left[\frac{im(\Delta x)^2}{2\hbar T} \right] $$
$$ (T=t-t_0,\Delta x = x-x_0) $$

確率密度分布
$$ \frac{m\Delta}{\sqrt{\pi}\left(m\Delta^2 + i\hbar T\right)} \exp\left[ -\frac{m\Delta^2x^2}{(m\Delta^2)^2+(\hbar T)^2} \right] $$

コーディング

定数は形に依存しないので
$$ \hbar = \Delta =\pi = m =1 $$
と考えてコードを書く

import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation

def _updateAnimation(frame):
    plt.cla()
    plt.ylim(-0.1,1.01)
    t = frame
    x = np.arange(-1*10,10,0.1)
    y = function(x,t)
    xline  = [0 for i in x]
    plt.plot(x,y)
    plt.plot(x,xline,color="black")
    t = round(t, 2)

def function(x,t):
    a = 1/(1+t**2)
    b = np.power(a,1/2)
    f = b*np.exp(-a*np.power(x,2))
    return f

def main():
    fig = plt.figure()
    params = {
        'fig':fig,
        'func':_updateAnimation,#グラフ更新する関数
        'interval': 100,#更新間隔
        'frames': np.arange(0,6, 0.05),#フレーム番号を生成するイテレータ
        'repeat': True,#繰り返しの有無
    }
    anime = animation.FuncAnimation(**params)
    anime.save("plot.gif", writer = 'imagemagick')
    plt.show()

if __name__ == '__main__':
    main()

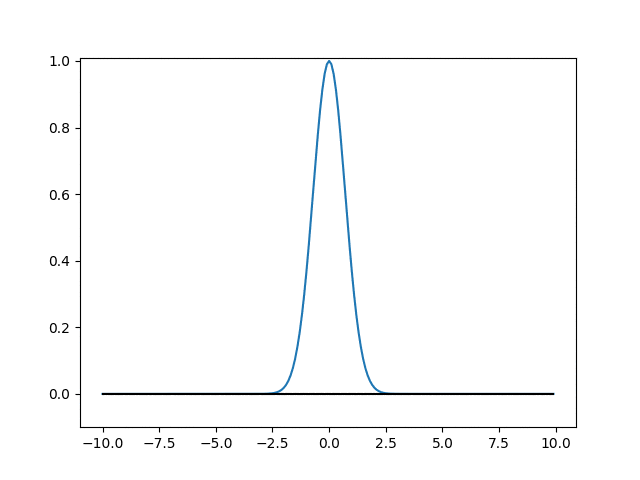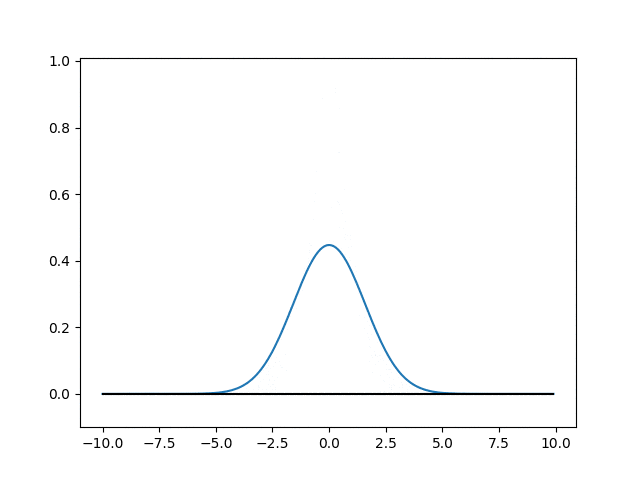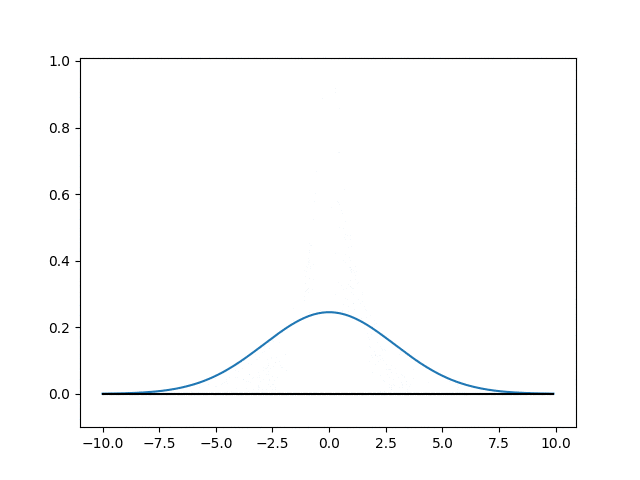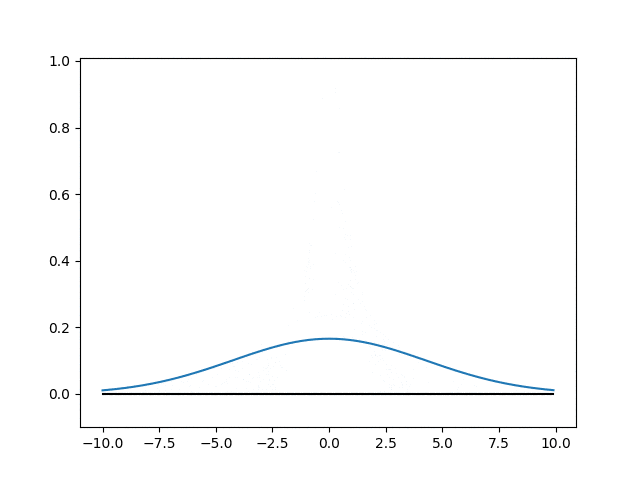
出力結果

考察

当然ながら時間経過とともに確率密度分布の裾ひろがって行きます。
このようにディラックのブラケットを用いた議論で考えた量子力学が系の状態変化をよく記述できていることが確認できました。

[追記]
波動関数の時間発展を見ても波動関数は単なる情報でしかないので実際に物理と照らし合わせるのであれば確率密度$ \left| \Psi(t,x) \right|^2 $ をプロットした方が評価として妥当でした．