はじめに
今回はレコメンダシステムのxDeepFMを紹介していきます。元の論文はここから確認できます。
概要に入る前に簡単にFactorization Machinesの説明をします。既知の場合は「概要」まで飛ばしてください。
機械学習の分野では特徴量エンジニアリングが重要になり、その中の一つに"cross features"や"multi-way features"と呼ばれる手法があります。たとえば$x_1,x_2$を説明変数としたとき、$x_1*x_2$を新たな説明変数として用いることをcross featuresと呼びます。しかし、正しいcross featuresを得るにはドメイン知識が必要ですし、変数が多いデータでcross featuresを行うことは実現性がありません。また、このようにして作ったcross featuresは未知の変数の相互作用は説明できません。
そこで、Factorization Machine(FM)があります。各特徴i(m-dim)をmよりずっと小さい次元であるD次元の潜在要素ベクトル$v_i=[v_{i1},v_{i2},\cdot\cdot,v_{iD}]$に埋め込み、特徴の相互作用を$f(i,j)=<v_i,v_j>x_ix_j$で表現します。この論文では$v_{i1}$をbitと呼びます。
しかし、FMの欠点は有用でない組み合わせの特徴の相互作用を生み出し結果を悪くしてしまうことにあります。そこで特徴量の表現力が強いDNNを使おうとするモデルが生まれました。DNNを活用したFNNとPNNは、しかし、高次元の特徴量の相互作用に焦点を当てており、低次元の特徴量の相互作用をあまり捉えることができていませんでした。そこでWide&DeepとDeep FMはそのような問題点を解決しました。しかし、DNNは高次元の特徴量の相互作用を暗示的に行なっているため、特徴の相互作用がどの次元まで行われているかに関する理論的帰結はありません。さらに、FMはベクトルワイズに特徴を作用させるのに対してDNNはbitワイズに作用させるため、DNNが果たして効果的なのかは疑問が残っています。そこで今回の論文では明示的でベクトルワイズな特徴の交互作用を学習するニューラルネットワークモデルを提案します。今回のモデルはDeep & Cross Networkに基づいていますが、このモデルは特別な形の交互作用のみ捉えることしかできません。今回扱うxDeepFMは高次元の明示的な交互作用と暗示的な作用と伝統的なFMを組み合わせたモデルになり、これらの問題の解決をはかります。
概要
Embedding Layer
Embedding Layer(埋め込み層)はone-hot encodingなどの特徴を低次元で密なベクトルにします。
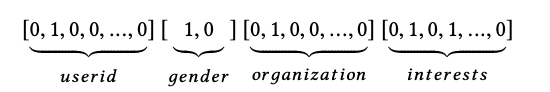
ここで、上の画像の例を見てみましょう。これはone-hot encodingで書かれている特徴で、useridやgenderはfieldです。一方、1578のような具体的なuser idやmaleというのはfeatureになります。
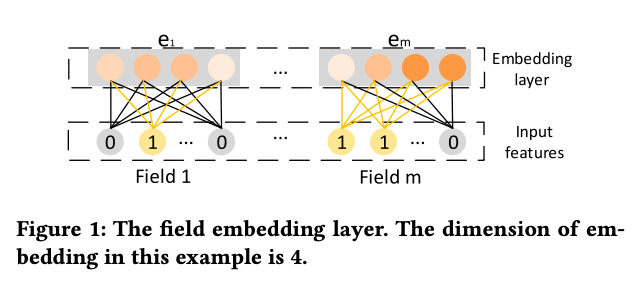
Embedding layerはe=[$e_1,e_2,\cdot,\cdot,e_m$]というベクトルを出力します。ここで、mはfieldの数で$e_i$は、あるfieldのembeddingを表します。one-hot encodingでは各field内のfeatureの数はまちまちでしたが、embeddingの場合は長さは同じになります。
暗示的な高次元の交互作用
暗示的な高次元の特徴の交互作用は以下のようにして学習していきます。
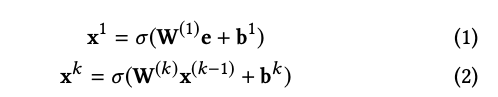
ここで、kは層の深さで$\sigma$は活性化関数です。これは下の図で"FM layer or Product Layer"の部分を取り除いたものになります。
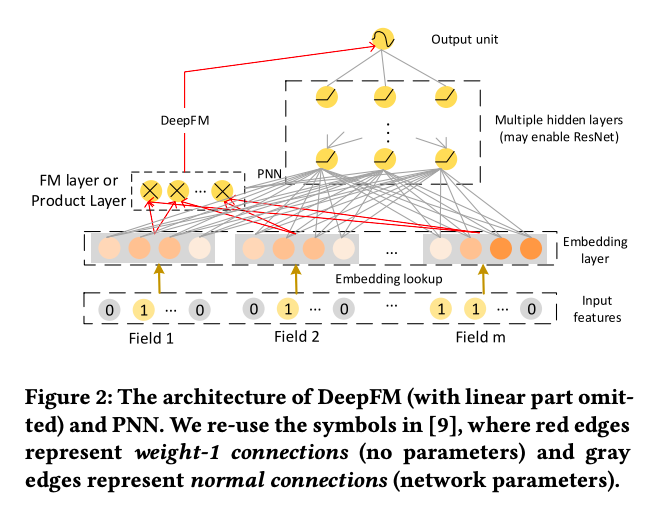
PNNとDeep FMは上記の構造に加え、two-wayのベクトルワイズの交互作用を明示的に加えてます(上図のFM layer or Product Layerにあたります)。PNNはproduct layerの出力をDNNに加えるのに対して、Deep FMはFM layerを直接output unitに接続しています。
明示的な高次元の交互作用
CrossNetは明示的な高次元の特徴の交互作用を可能にしています。隠れ層は以下のように計算されています。
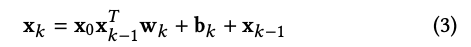
下図はこの式を図示したものになります。
ここで、cross networkのk層目の出力$x_k$は$x_0$のスカラー倍になります。
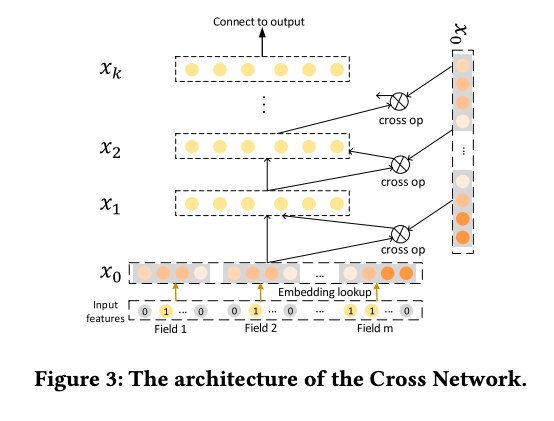
しかし、CrossNetの欠点は各隠れ層が$x_0$のスカラー倍にしかならない点やbit wiseで交互作用を求めている点にあります。
Compressed Interaction Network
今回扱うxDeepFMはCINというネットワークを持ちます。CIN(Compressed Interaction Network)は以下の特徴を持ちます。
- ベクトルワイズで交互作用を求める
- 高次元の交互作用が明示的である
- 交互作用の次元が増えても複雑さが指数的に増えない
field embeddingの出力を$X^0$とすると、$X_{i,*}^0=e_i$となり、Dはfield embeddingの次元になります。CINのk層目の出力は$X^k\in \mathcal{R}^{H_k\times D}$となります。$H_k$はk層での特徴ベクトルの数で$H_0=m$になります。
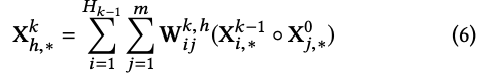
ここで、$1\leq h\leq H_k$,$W^{k,h}\in \mathcal{R}^{H_{k-1}\times m}$はh番目の特徴ベクトルに対するパラメーターです。◦ はHadamard productで⟨a1, a2, a3⟩◦ ⟨b1,b2,b3⟩ = ⟨a1b1, a2b2, a3b3⟩となります。ここで$X^k$は$X^{k-1}$と$X^0$の明示的な交互作用により導き出され、交互作用の程度は層の深さとともに増えていきます。embedding vectorの構造を保ったままの交互作用なので、ベクトルワイズになっています。
このCINはCNNのように捉えることができます。
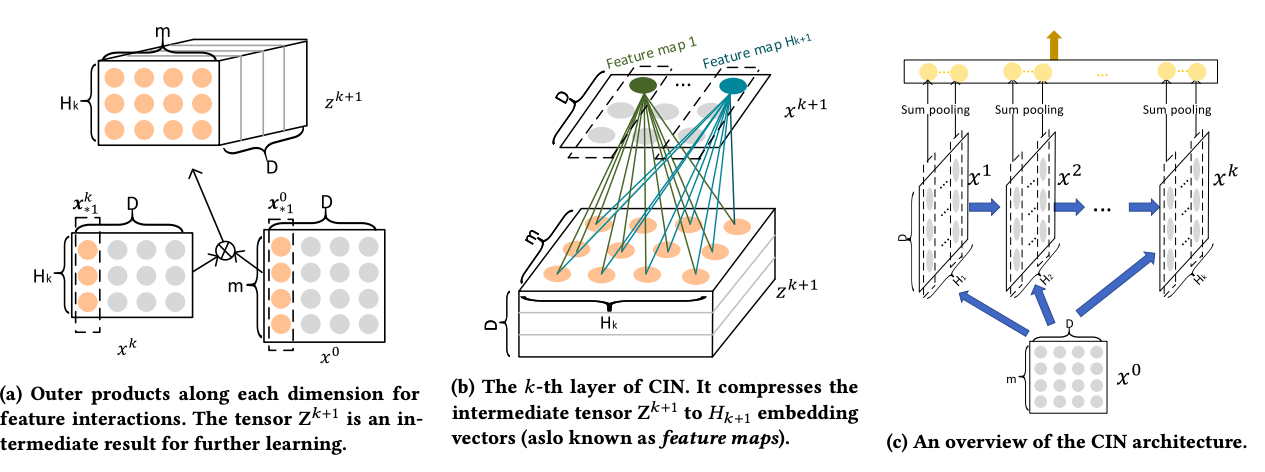
$X^k$と$X^0$の外積の結果を$Z^{k+1}$とすると、これを画像として扱うことができます。そして$W^{k,h}$はfilterになります。filterは$Z^{k+1}$のembedding次元 (D)に沿ってスライドさせます。$X_{i,*}^{k+1}$ はfeature mapと呼ばれます。そのため、$X^{k+1}$は$H_{k+1}$の異なるfeature mapの集合になります。
次は上図の(c)を参照してください。全ての隠れ層$X^k$はoutput unitと繋がりがあります。まず、各隠れ層のfeature mapのsum poolingを適用します。

ここで$i\in [1,H_k]$。こうしてpoolingベクトル$p^k=[p_1^k,p_2^k,\cdot,\cdot,p_{H_k}^k]$を得ます。全ての隠れ層からのpoolingベクトルはoutput unitのまえで結合され、$p^{+}=[p^1,p^2,\cdot,\cdot,p^T]\in \mathcal{R}^{\sum_{i=1}^T H_i}$となります。もし、CINをバイナリーの分類に用いるとしたら、output unitは
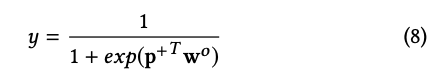
となります。
CINの分析
Space Complexity
CINの合計のパラメーターの数は$\sum_{k=1}^{T}H_k\times(1+H_{k-1}\times m)$となり、embedding次元Dからは独立です。一方で、T layersのDNNは$m\times D \times H_1 + H_T+\sum_{k=2}^{T}H_k\times H_{k-1}$個パラメーターがあり、これはembedding次元Dとともに増加します。たいてい、mと$H_k$は大きくないので、$W^{k,h}$のスケールは許容されます。ただ必要な場合は、L orderの分解が可能で$U^{k,h}\in \mathcal{R}^{H_{k-1}\times L}$と$V^{k,h}\in \mathcal{R}^{m\times L}$を用いて、
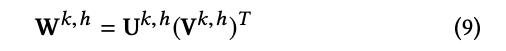
と表せます。ここで、L<<H, L<<mです。今後、各隠れ層はある一定の数だけのfeature map(H個)を持つと仮定します。L order分解でspace complexityは$O(mTH^2)$から$O(mTHL+TH^2L)$に減らせます。
Time Complexity
テンソル$Z^{k+1}$を計算するコストは$O(mHD)$時間で、T LayerのCINの計算は$O(mH^2DT)$時間かかります。一方で、T LayersのDNNは$O(mHD+H^2T)$時間でCINの方がコストが高いことがわかります。そのため、CINの欠点はtime complexityにあることがわかります。
Polynomial Approximation
演繹的にk層目のh番目のfeature mapは以下のように表せることがわかります。
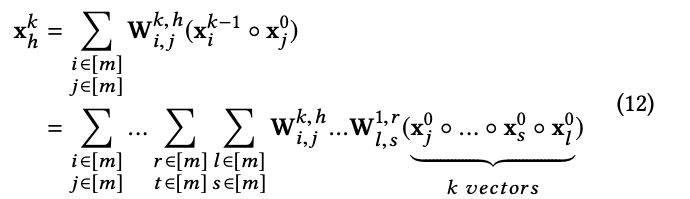
従来のpolynomialは$O(m^k)$係数がありましたが、CINでは$O(km^3)$でpolynomialを近似できます。
Combination with Implicit Networks
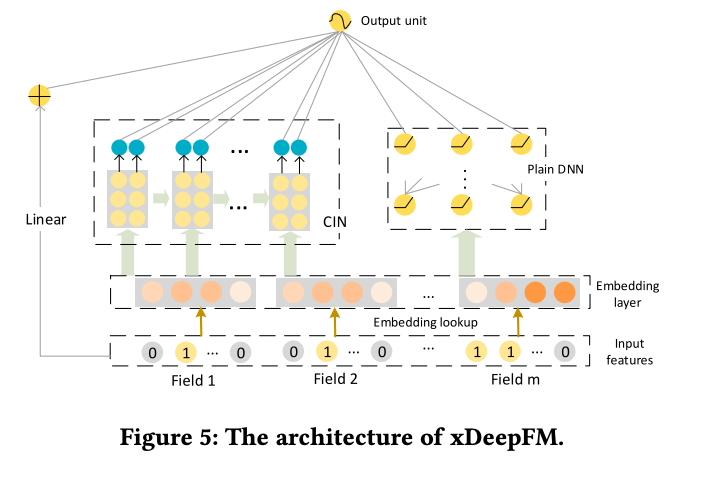
普通のDNNは暗示的な特徴の相互作用を学習するため、CINとDNNはお互いを補う合う関係にあるといえます。両者を結合することでモデルをより強くすることができます。xDeepFMのoutput unitは結果として以下のようになります。
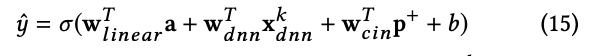
ここで、$\sigma$はシグモイド関数で、aはinput featuresで$x_{dnn}^k,p^{+}$はそれぞれDNNの出力とCINの出力になります。
損失関数は以下のようになります。
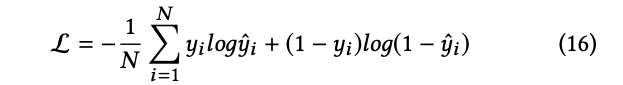
最適化は以下の目的関数を最小化することで行われます。
