本記事は，SP2LC Advent Calendar 2017の３日目として書いたものです．

SP2LCとの関わり

SP2LCには1年生の後期から顔を出し始めて，何人かの先輩からプログラミングを教えてもらっていました．
本格的な活動としては2年生に参加した全国高専プログラミングコンテストの競技部門からで，そこからは4年連続プロコンに参加し，実際に選手として２回は登壇しています．

専攻科に入ってからは，後輩である彩希くん，北村くん，丸尾くん，水野くんにデザイン科の内村さんを含めたチームでImagin Cup2017への参加を目指したりもしました．

はじめに

サレジオ高専では，5年生における卒研が非常に重要ですし，仮に専攻科に進学するのであれば研究活動の重要性はより高まってきます，タイトルにあるような”最適化問題”や”GA(遺伝的アルゴリズム)”はまさしく僕の研究で直面しているキーワードたちですが，それはすなわちサレジオ高専における研究活動…特に，内田先生の計算システム研究室や，島川先生の数理モデル研究室…でも頻繁に取り扱われる問題ということになります．

この記事は，今ちょうど研究室選びに悩んでいるであろう4年生たちが思うような「先輩って何してんの？」という疑問に技術的なアプローチで答えようとするものです．結果として，この記事が研究室選びや研究テーマを考える上での助けになればと思います．

最適化問題ってなんぞや

最適化問題（さいてきかもんだい、英: optimization problem）とは、特定の集合上で定義された実数値関数または整数値関数についてその値が最小（もしくは最大）となる状態を解析する問題である。

これはWikipediaの引用で，とてもわかりやすい記述ですね，
この引用を言い換えて関数 $f(x)$ が最大値となる $x$を探す問題とか言ってもいいかもしれません．この時の関数$f$は一般に目的関数と呼び，$x$がどういう条件の引数か決めるものを制約条件，実際の引数$x$を可能解，そして$f(x)$が最大値をとる$x$を最適解と呼んだりします．

情報科の授業で習うであろう線形計画問題や整数計画問題などといった問題も最適化問題に含まれます．これらの問題の数学的な記述，あるいはこれらを解くための線形計画法やニュートン法などのアルゴリズムは授業で触れますから，今回一切触れません．僕は多目的最適化の話がしたいのです．

しかし，もう少し感覚的に最適化問題について知るためにNTTから引用した素晴らしい図を示します．

この図を見ると，制約条件に従った引数$x$を実行可能領域として横軸にとり，それに対応する関数$f$の値を縦軸にとっていますね．このような概念的なプロットは最適化問題を説明する際によく用いられ，解空間と呼ばれることもあります．
この図はたった１変数の非線形関数で説明していますが，実際の実問題においては，現実的な時間で実行可能領域を網羅的に調べることはできません．なので最適化問題においては，最適解に可能な限り近い$x$を知るために，この解空間を効率的に探索する手法について考えることがとても重要です．
そして現に，計算システム研究室に所属する僕なんかはそんな問題を研究として取り組んでいます．

多目的最適化ってなんぞや

その名の通り，多目的な最適化問題のことです．
先ほどでは一つの目的関数を満たす最適解が欲しいだけでした．しかし，時には複数の目的関数を同時に満たすような一つの解が知りたくなる時があります．しかもその目的関数たちは，相関がない時もありますが，時にはトレードオフの関係だったりします．

こういうこと，よくありますよね．あっちを立てればこっちが立たず，みたいな状況です．そんな時にいい塩梅の答えが欲しい時は，多目的最適化アルゴリズムについて考える必要性があるでしょう．

多目的最適化は関数が複数あり，前述した解空間のプロットは示しづらいので，よく以下のような図が用いられます．(またNTTから引用，時間なくて図を作れない)

これは２目的の最適化問題における説明で，縦軸を目的関数$f_1$，横軸を目的関数$f_2$でとっていますね．つまり各点が可能解ということになり，この解の良し悪しは$f_1$をy座標，$f_2$をx座標として考え，(0,0)からのマンハッタン距離で決まるということです．
２つの目的関数がそれぞれ最小となる解が欲しいところですが，図を見ての通り，マンハッタン距離が同じ解が複数存在しますね，２つの関数はトレードオフの関係になってることが多いので，苦肉の策としてマンハッタン距離が最も短い解集団(=パレート最適解)を得ることが多目的最適化アルゴリズムの目的となります．

NSGA-Ⅱアルゴリズム

世の中に多目的最適化アルゴリズムはいくつか存在しますが，NSGA-Ⅱはその一つで，これは遺伝的アルゴリズム(GA)を多目的に拡張したものです．

実際のところ，単純なGAは相当にレガシーな手法で，私がやっているような画像の最適化といった，解と解の間に全く相関がない最適化問題は苦手とするところです．また，近年においてはCNNの発展もめざましく，実問題，特に画像処理に応用される研究はずいぶん少なくなってきました．

しかし，多目的な最適化については，ニューラルネットワークの応用はあまり研究が進んでいないというのが私見であり，多目的最適化アルゴリズムの中でも，NSGA-Ⅱは代表的な手法の一つです．

遺伝的アルゴリズム(GA)の基本的なアイディア

GAは最適化問題をメタヒューリスティック的に解く代表的な手法です．NSGA-Ⅱについて紹介する前に，これを用いて最適化問題を解く基本的なアイディアについて触れましょう．GAは主に以下のような手順で実行されます．

GAにおける個体とは，解を表します．つまり，目的関数 $f(x)$の最適解が知りたい際には，GAの個体は任意の可能解 $x^,$を持っている，ということです．

まず，初期集団の生成では，この個体をランダムに，複数個生成します．制約条件の中でテキトーにサイコロを振って，その値を個体にしてしまうわけですね．それをたくさん用意して母集団とします．
次に，個体の評価を行います．ここで，母集団に含まれるすべての個体がランダムな解を持っているわけですが，目的関数$f$に個体の解を代入した戻り値を個体の評価値として与えます．
次は選択操作です．ここでは母集団中の個体同士で戦ってもらいます．弱肉強食ですね．良い評価値を持つ個体が生き残り，雑魚い個体は淘汰されます．
遺伝的操作は母集団の個体に直接改変を加える操作です．個体を２つピックアップして組み合わせる交叉や，個体の一部分を一定の割合でランダムに変化させる突然変異などです．
ここまで終わればまた個体の評価に戻ります．ここで，世代数が指定した数に到達するか，もしくは欲しい評価値を持つ個体が見つかれば，終了です．

このように，GAは複数の解を運に任せて進化させることで，実用的な解を得ることのできる手法です．

NSGA-Ⅱの流れ

NSGA-ⅡはGAを多目的に拡張するために，相応に複雑なアルゴリズムになっています．そのため，その解説は変数とステップで示したいと思います．読むのがしんどいかもしれませんが，その代わり，きちんと読みさえすれば簡単にコードに起こすことができるようになるはずです．おそらく．

変数リスト

世代数 $t$
- NSGA-Ⅱは遺伝的アルゴリズムと同じように，解を表す個体を複数個生成して母集団とし，それを進化させることで最適解を得ます．これは世代数を表す変数．
初期探索母集団 $Q_t$
- NSGA-Ⅱは２つの母集団を持ち，これは遺伝的オペレータを適用する母集団として用います．
アーカイブ母集団 $P_t$
- もう一つの母集団は，次世代に残したい優良個体を選別して保存しておくための母集団です．

アルゴリズムの流れ

世代数 $t=1$ とする．初期探索母集団 $Q_t$ を個体数 $N$ で初期化し，アーカイブ母集団 $P_t$ を空にする．
$Q_t$ の各個体の評価値を目的関数を用いて評価．
$R_t=Q_t \cup P_t$を作成する．$R_t$に対して非優先ソートを実行し，全個体をランク毎に分類：$F_i,i=1,2,..,etc$
新たに $P_{t+1}= \emptyset$ を作成し，$i=1$とする，$|P_{t+1}|+|F_i|<N$ を満たすまで $P_{t+1}=P_{t+1}∪F_i,i=i+1$ を実行．
混雑度ソートを実行し，$F_i$の中でもっとも多様性に優れた個体を$N-|P_{t+1}|$個，$P_{t+1}$に加える．
$t$が指定の世代数に到達した場合，終了する．
$P_{t+1}$をもとに，混雑度トーナメント選択によって新たな探索母集団$Q_{t+1}$を生成する．
$Q_{t+1}$に対し，交叉，突然変異の遺伝的操作を行う．$t=t+1$とし，2に戻る．

このように，NSGA-Ⅱは２つの母集団を組み合わせた$R_t$から次世代のアーカイブ母集団 $P_t$を作成し，また次世代の探索母集団$Q_t$を，非優先ソートと混雑度ソート，そして混雑度トーナメントを用いることで決定しています．

非優先ソートによるランキング

非優先ソートは集団の個体を，理想的な解である(0,0)へのマンハッタン距離ごとにランクづけし，分類するために行います．
1. ランク$r=1$とする．
2. $R_t$のなかで，(0,0)へのマンハッタン距離が最も短い個体を選び，これらの個体を$F_r$に格納する．
3. 格納した個体を$R_t$から覗き，$r=r+1$ とする．
4. $R_t$が空になるまで2,3を繰り返す．

混雑度ソート

混雑度ソートは，ある個体$i$の周囲にある個体が，どの程度密集しているか評価するために行います．これも非優先ソートと同様にステップで示しますが，少々複雑です．
1.　ランク$r=1$とし，$l=|F_r|$とする．また，$F_r$の各個体$i$に，混雑度$d_i=0$を設定する．
2.　２つの目的関数の集合$m=1,2$ に対して，各目的関数の評価値が悪い順に個体をソートする : $I^m=sort(f_m,>)$
3.　各目的関数$m=1,2$におけるソート $I^m$に対し，境界個体に無限距離を与える：$d_{I^m_1}=d_{I^m_l} = \infty$
4.　境界以外の個体$(j=2,,,,l-1)$に対して，以下の式で混雑度計算を行う(なぜかこの式だけQiitaだとTexをコピペすると崩れるので画像です)

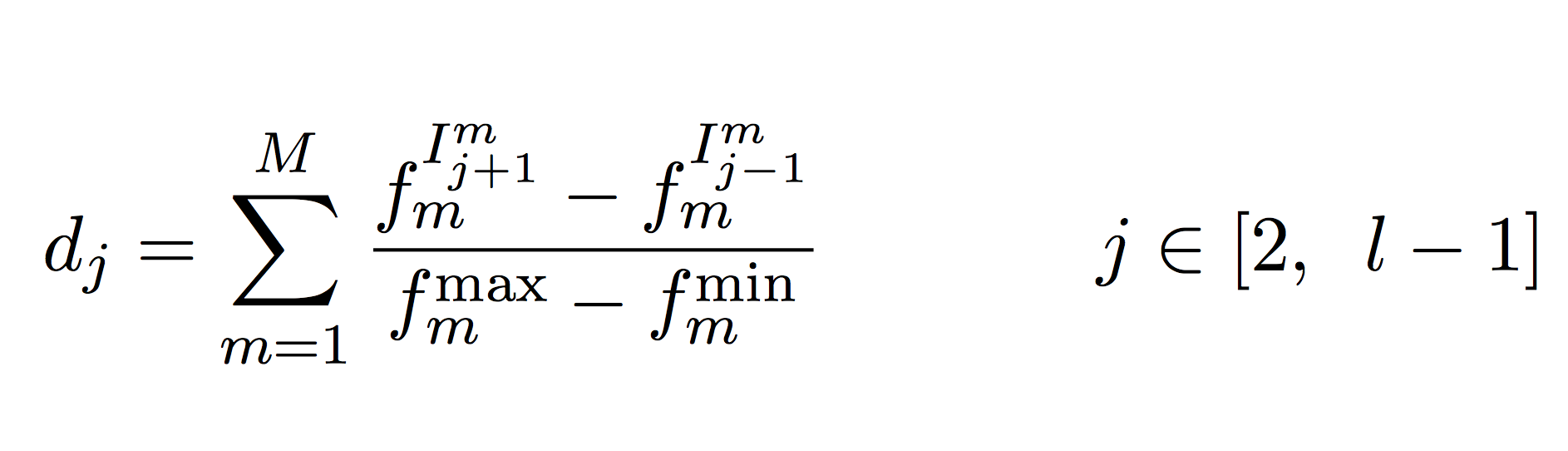
混雑度トーナメント

混雑度トーナメントでは，母集団の個体$i$が持つ以下の２つの基準でトーナメント選択を行います．

個体のランク $i_{rank}$
個体の混雑度距離 $i_{distance}$

母集団から2つの個体 $i$ と $j$ をランダムに選択し，以下のいづれかの基準を満たせば $i$は$j$より優れているとして，次の母集団に加得ます．．

$i_{rank} < j_{rank}$
$i_{rank}=j_{rank}$ and $i_{distance}>j_{distance}$

このように，NSGA-Ⅱは非優先ソートによるパレート解集合の精度向上と，混雑度距離を基準とした多様性の維持を行うことで，精度と均一性を高めるメカニズムが採用されていて，これによって２つの目的関数が作り出す複雑な解空間の探索が行えます．

まとめ

ここまで，最適化問題とその多目的への拡張，及びそれを探索するNSGA-Ⅱアルゴリズムについて紹介してきましたが，実際の研究においては，これを実問題に適用するようなシチュエーションが多くなってきます．
つまり，より具体的な問題，画像の最適化や，フィルタの最適化，通信経路設計の最適化であったり，もしくは，株券の購入タイミングの最適化もあるかもしれません．

僕なんかは，CT画像再構成に適用してますから，画像の最適化をしているわけです．特にCTは，得られるX線計測データと実際の画像の間に周波数空間と時間空間を行き来する関係があることが知られているため，２つの空間それぞれに存在する目的関数を同時に満たす画像が欲しいのです．ここでNSGA-Ⅱといった多目的な最適化アルゴリズムを用いるわけですね．

言ってしまえば計算システム研究室と数理モデル研究室は最適化問題の研究室です(もちろん他のこともできる)．どちらの研究室においても，実問題をどうやって最適化問題に落とし込めるか，が鍵となり，計算システム研究室ではそれを，計算資源を最大限用いたメタヒューリスティック的手法で解いてみる，もしくは手法を改良してみる，といったことに取り組むことが多く，数理モデル研究室では，その問題を計算理論として扱えるような定式化に取り組むことが多い，というのが私見です(もちろんOB/OGでこの範疇の外で，素晴らしい様々な研究をした方もいらっしゃいます)．

少なくとも，計算システム研究室で3年にわたり研究をしてきた僕は，今日ここで書いたような技術を用いてダラダラと研究をしているわけです．後輩たちは是非，こんな前例を研究室選びの一助にしていただき，実りある卒研を遂行できるよう頑張っていただきたいと思っています．

多目的な最適化問題を解くためにNSGA-Ⅱを解説する