グラフアルゴリズム入門 : 最小全域木 (MST)

Posted at 2025-01-16

はじめに

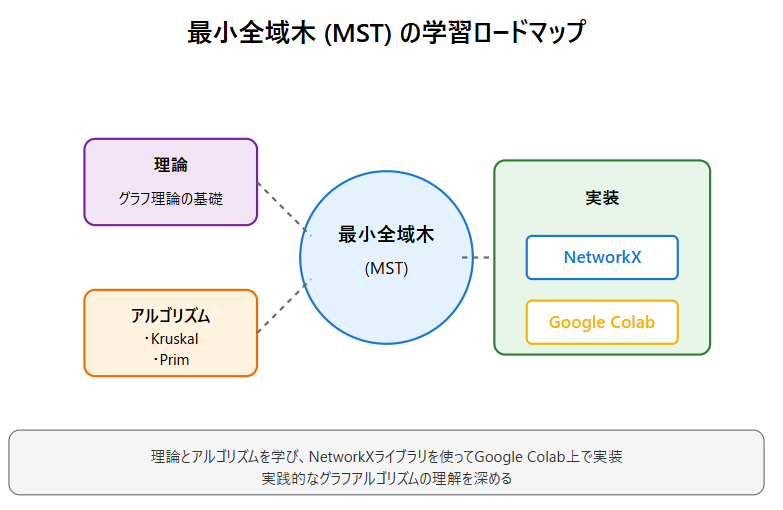
この記事では、最小全域木 (Minimum Spanning Tree, MST) の概念と理論、具体的なアルゴリズム (Kruskal/Prim) を解説します。また、Python の NetworkX ライブラリを用いた実装例を紹介し、Google Colab 上で簡単に実行可能なサンプルコードを提供します。

1. 最小全域木とは？

定義

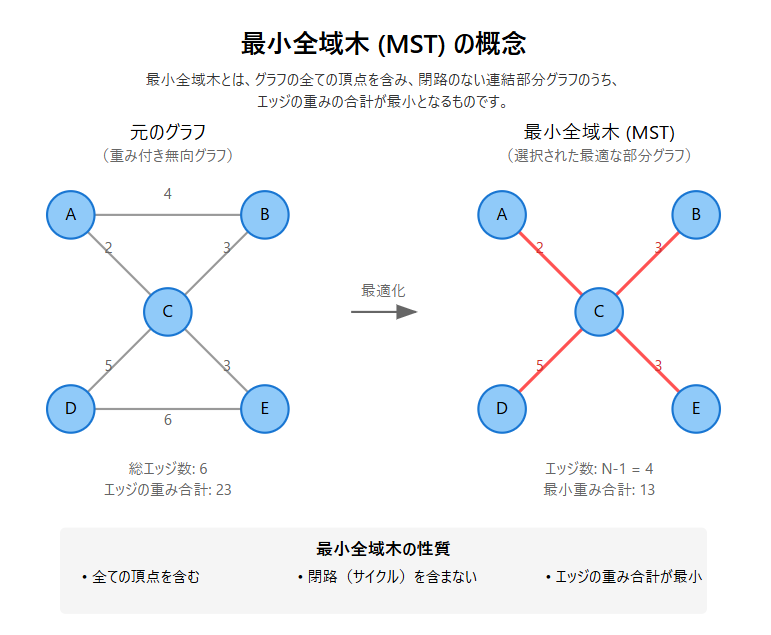
全域木 (Spanning Tree): グラフの全ての頂点を繋げるが、閉路 (サイクル) を含まない部分グラフ。
最小全域木 (MST): 全域木の中で、エッジの重みの合計が最小となるもの。

応用例

ネットワーク設計: ケーブルの長さやコストを最小限に抑えた配線計画。
クラスタリング: 最も長いエッジをカットしてクラスタを分ける手法。
画像セグメンテーション: 画像をグラフとして扱い、セグメント化を行う。

2. MST を求めるアルゴリズム

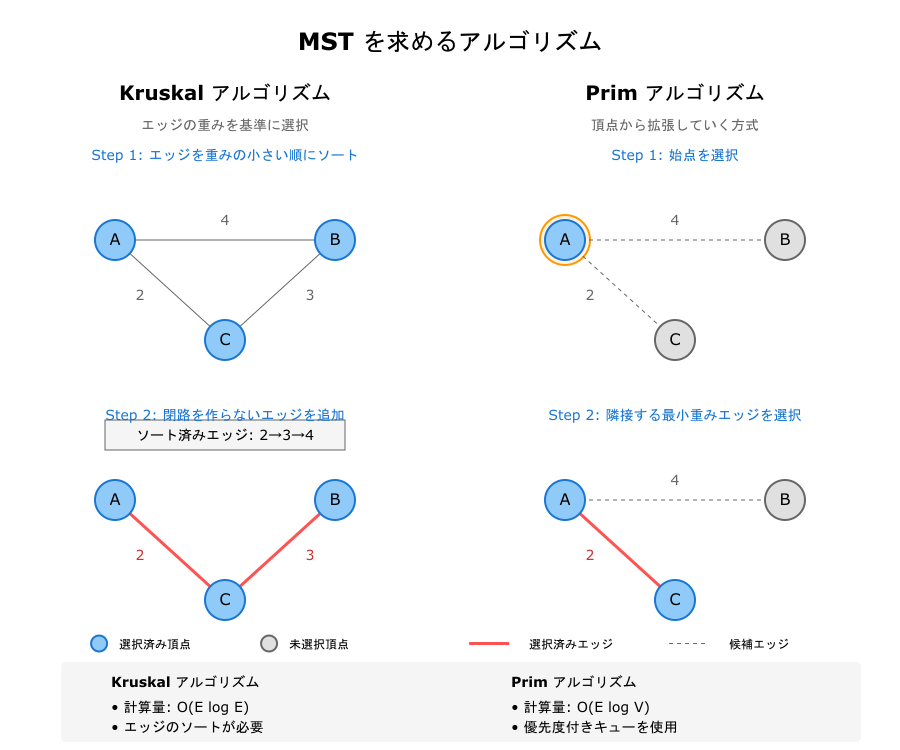
2.1 Kruskal アルゴリズム

全てのエッジを重みの小さい順にソートする。
順にエッジを取り出し、閉路ができない場合に採用する。
エッジ数が ( V-1 ) 本になるまで続ける。

計算量:

( O(E \log E) ) (エッジのソートがボトルネック)。

2.2 Prim アルゴリズム

任意の頂点を選び、木 (MST) を開始する。
現在の木に接続可能な最小重みのエッジを選ぶ。
全ての頂点が含まれるまで繰り返す。

計算量:

( O(E \log V) ) (優先度付きキューを用いる場合)。

3. NetworkX を使った実装例

以下のコードは Python の NetworkX を使って MST を求める例です。Google Colab などでコピー＆ペーストして実行できます。

# Install necessary libraries (if running on Google Colab)
!pip install networkx matplotlib

# Import libraries
import networkx as nx
import matplotlib.pyplot as plt

# Create a graph
G = nx.Graph()

# Add nodes and weighted edges
G.add_edges_from([
    ("A", "B", 4), ("A", "C", 2), ("B", "C", 1), 
    ("B", "D", 5), ("C", "D", 8), ("C", "E", 10), ("D", "E", 2)
])

# MST の計算
# デフォルトでは Kruskal アルゴリズムが使用されます
mst = nx.minimum_spanning_tree(G)

# Prim アルゴリズムを使用する場合は以下のいずれかを使用します
# mst = nx.minimum_spanning_tree(G, algorithm='prim')

# Print edges in the MST
print("Edges in the MST:", list(mst.edges(data=True)))

# Visualize the graph and MST
pos = nx.spring_layout(G, seed=42)
plt.figure(figsize=(8, 6))

# Draw the original graph
nx.draw(G, pos, with_labels=True, node_color='lightblue', edge_color='gray', node_size=800)
nx.draw_networkx_edge_labels(G, pos, edge_labels=nx.get_edge_attributes(G, 'weight'))

# Highlight the MST edges
nx.draw_networkx_edges(G, pos, edgelist=mst.edges, edge_color='red', width=2)
plt.title("Minimum Spanning Tree (MST)")
plt.show()

4. まとめ

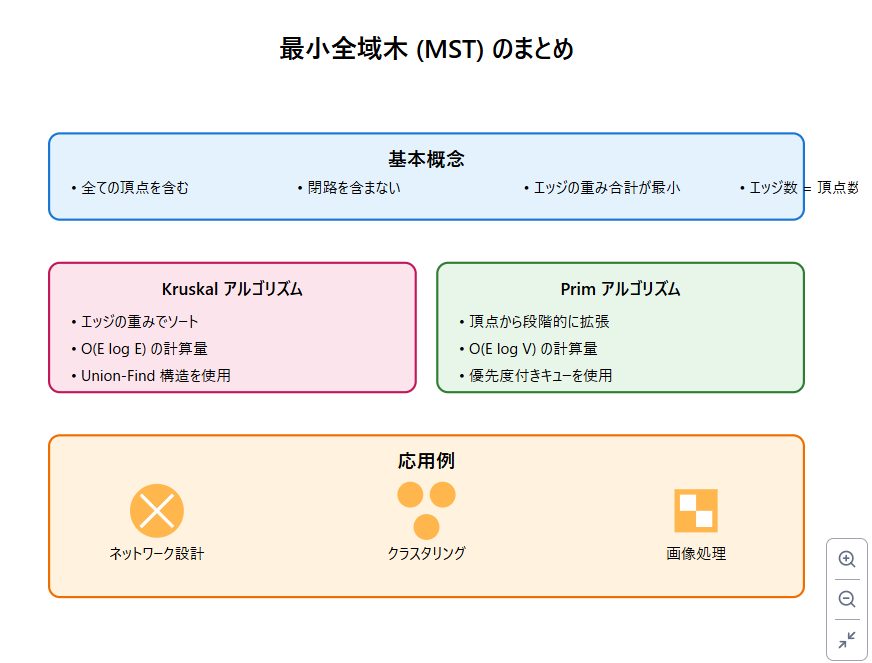
最小全域木 (MST) は、ネットワーク設計やクラスタリングなど、様々な応用が可能な重要な概念です。
Kruskal アルゴリズムと Prim アルゴリズムは MST を効率的に求める手法として広く使われています。
Python の NetworkX ライブラリを活用すると、MST の計算と可視化が簡単に行えます。

参考文献

実装例: ノートブック


{
 "cells": [
  {
   "cell_type": "markdown",
   "id": "c9b2b726",
   "metadata": {},
   "source": [
    "# Minimum Spanning Tree (MST) Example with NetworkX"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "id": "5f0dd9ad",
   "metadata": {},
   "outputs": [],
   "source": [
    "\n",
    "# Install necessary libraries (if running on Google Colab)\n",
    "!pip install networkx matplotlib\n"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "id": "88c0d7be",
   "metadata": {},
   "outputs": [],
   "source": [
    "\n",
    "# Import libraries\n",
    "import networkx as nx\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "# Create a Graph object\n",
    "G = nx.Graph()\n",
    "\n",
    "# Add nodes (labeled in English letters)\n",
    "G.add_nodes_from([\"A\", \"B\", \"C\", \"D\", \"E\"])\n",
    "\n",
    "# Define edges as (node1, node2, weight)\n",
    "edges = [\n",
    "    (\"A\", \"B\", 4),\n",
    "    (\"A\", \"C\", 2),\n",
    "    (\"B\", \"C\", 1),\n",
    "    (\"B\", \"D\", 5),\n",
    "    (\"C\", \"D\", 8),\n",
    "    (\"C\", \"E\", 10),\n",
    "    (\"D\", \"E\", 2)\n",
    "]\n",
    "\n",
    "# Add edges with weights\n",
    "for u, v, w in edges:\n",
    "    G.add_edge(u, v, weight=w)\n",
    "\n",
    "# Calculate the Minimum Spanning Tree\n",
    "mst = nx.minimum_spanning_tree(G)\n",
    "\n",
    "# Extract edges from MST\n",
    "mst_edges = list(mst.edges(data=True))\n",
    "print(\"Edges in the MST:\", mst_edges)\n",
    "\n",
    "# Draw the original graph and MST\n",
    "pos = nx.spring_layout(G, seed=42)\n",
    "plt.figure(figsize=(8,6))\n",
    "\n",
    "# Draw the original graph in gray\n",
    "nx.draw_networkx(\n",
    "    G, pos, \n",
    "    node_color='lightblue', \n",
    "    edge_color='gray',\n",
    "    with_labels=True,\n",
    "    node_size=800\n",
    ")\n",
    "\n",
    "# Highlight MST edges in red\n",
    "mst_edge_list = [(u, v) for (u, v, d) in mst_edges]\n",
    "nx.draw_networkx_edges(G, pos, edgelist=mst_edge_list, edge_color='red', width=2)\n",
    "\n",
    "# Show edge weights\n",
    "edge_labels = {(u, v): d['weight'] for (u, v, d) in G.edges(data=True)}\n",
    "nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)\n",
    "\n",
    "plt.title(\"MST (Red edges represent the Minimum Spanning Tree)\")\n",
    "plt.axis('off')\n",
    "plt.show()\n"
   ]
  }
 ],
 "metadata": {},
 "nbformat": 4,
 "nbformat_minor": 5
}

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up