NetworkXで始める大規模グラフ処理の記事を書きました。10万ノードのグラフ生成から中心性計算、可視化まで5つのステップで解説しています。Barabási-Albertモデルを例に実践的なコード例も掲載。グラフ理論に興味ある方、ぜひご覧ください。🍛
はじめに
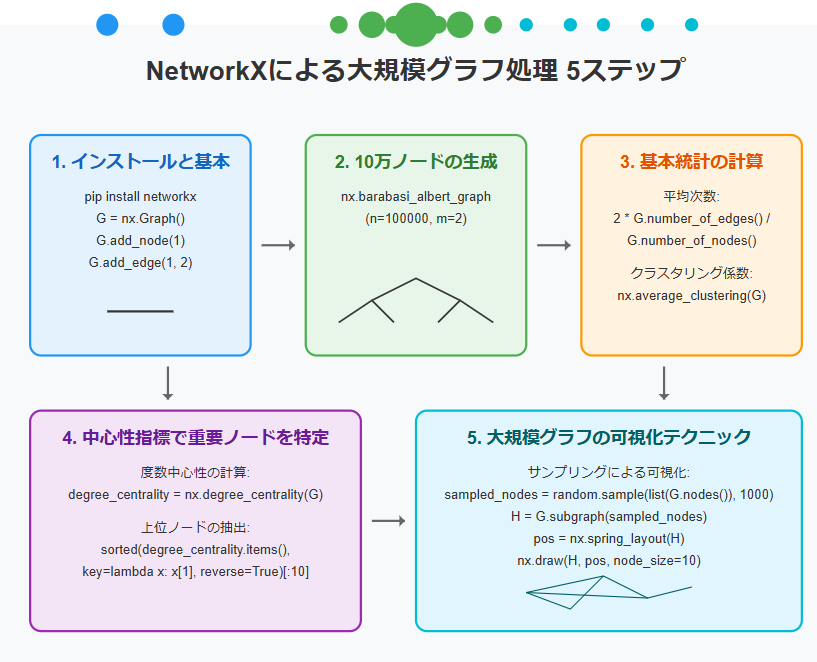
Pythonを使った大規模グラフ処理に興味はありますか?本記事では、NetworkXライブラリを使って、誰でも簡単に始められる大規模グラフ処理の方法を5つのステップで解説します。ソーシャルネットワーク分析や交通ネットワークの最適化など、様々な分野で活用できる技術を、初心者にもわかりやすく説明します。
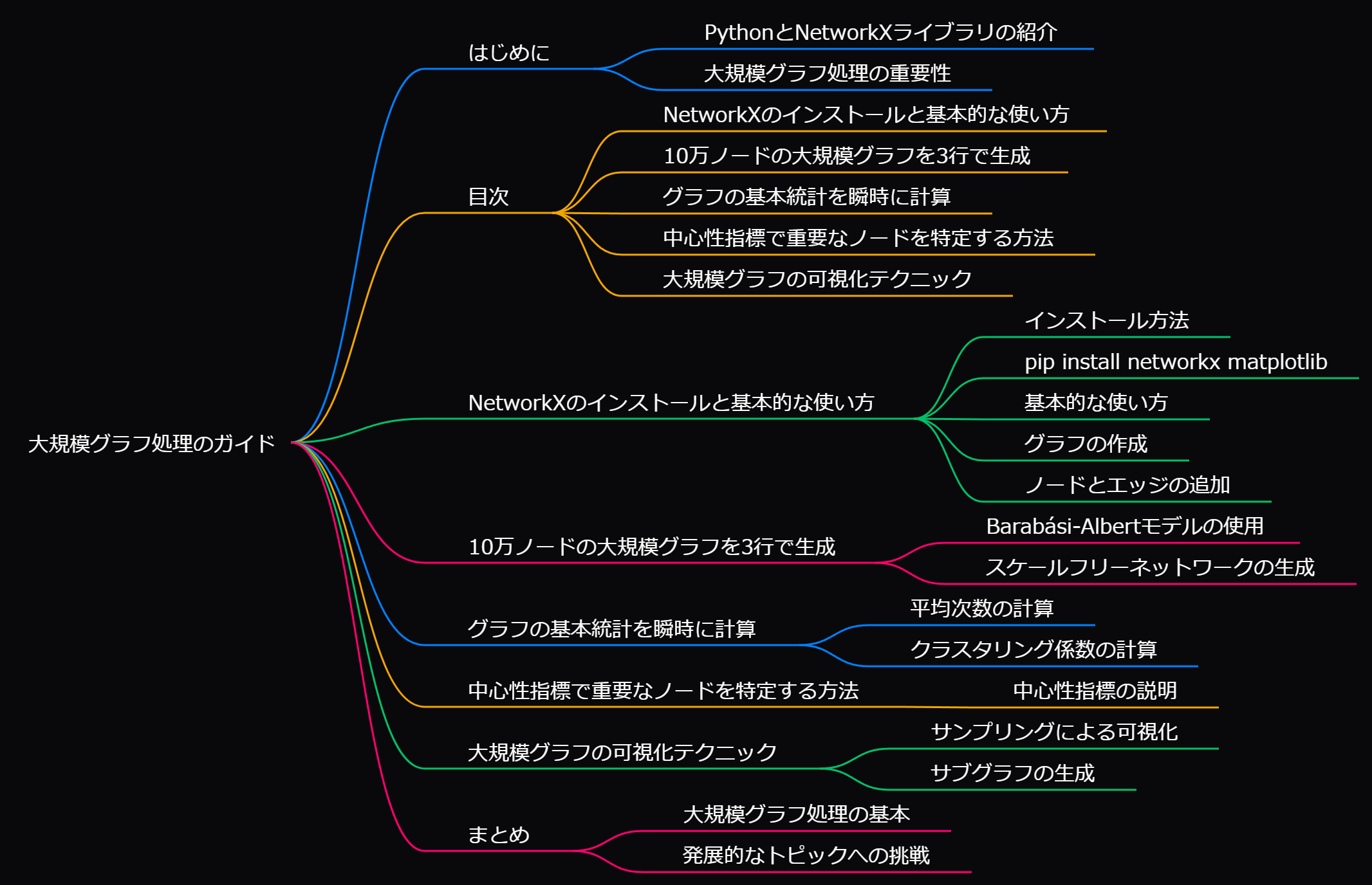
目次
- NetworkXのインストールと基本的な使い方
- 10万ノードの大規模グラフを3行で生成
- グラフの基本統計を瞬時に計算
- 中心性指標で重要なノードを特定する方法
- 大規模グラフの可視化テクニック
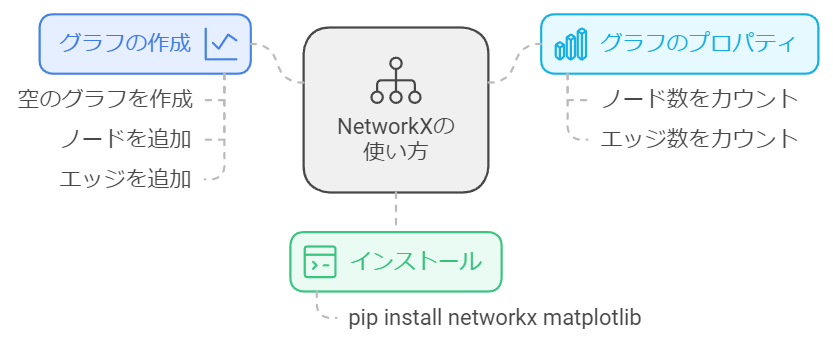
1. NetworkXのインストールと基本的な使い方
NetworkXは、Pythonでグラフ処理を行うための強力なライブラリです。インストールは、以下のコマンドで完了します。
pip install networkx matplotlib
基本的な使い方は以下の通りです:
import networkx as nx
# 空のグラフを作成
G = nx.Graph()
# ノードを追加
G.add_node(1)
G.add_node(2)
# エッジを追加
G.add_edge(1, 2)
print(f"ノード数: {G.number_of_nodes()}")
print(f"エッジ数: {G.number_of_edges()}")
出力例:
ノード数: 2
エッジ数: 1
2. 10万ノードの大規模グラフを3行で生成
大規模なグラフを簡単に生成できることは、NetworkXの大きな魅力の一つです。以下のコードで、わずか3行で10万ノードのスケールフリーネットワークを生成できます。
import networkx as nx
# 10万ノード、平均次数4のBarabási-Albertモデルを生成
G = nx.barabasi_albert_graph(n=100000, m=2)
print(f"生成されたグラフ - ノード数: {G.number_of_nodes()}, エッジ数: {G.number_of_edges()}")
出力例:
生成されたグラフ - ノード数: 100000, エッジ数: 199996
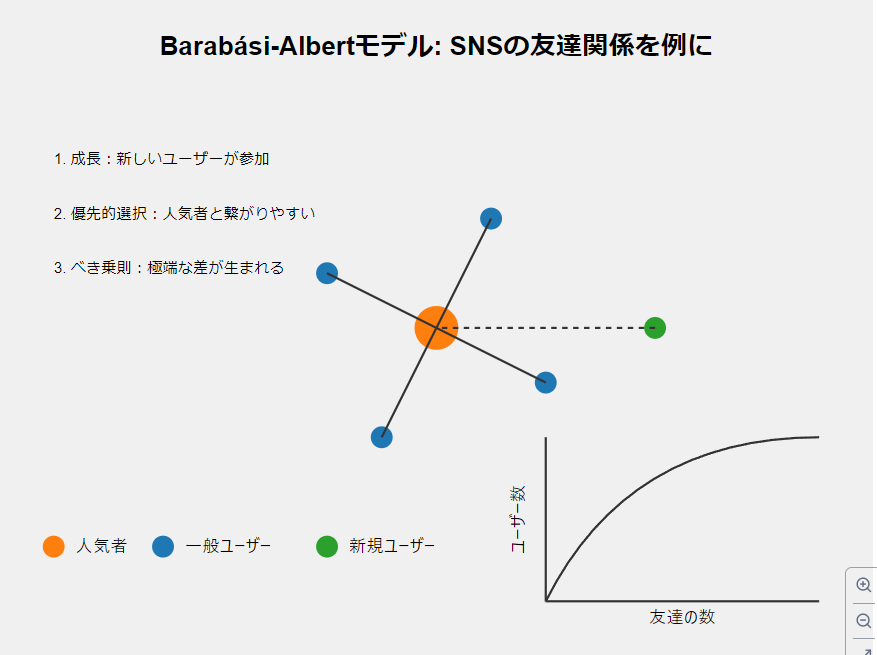
Barabási-Albertモデル:SNSの友達関係を例に
Barabási-Albertモデルは、現実世界のネットワークがどのように形成されるかを説明する考え方です。SNS(ソーシャル・ネットワーキング・サービス)の友達関係を例に説明してみましょう。
モデルの特徴
-
新しい人がどんどん参加する(成長)
- SNSに新しいユーザーが次々と登録していく様子を想像してください。
-
人気者効果(優先的選択)
- 新しく参加した人は、すでに多くの友達がいる人(人気者)とつながりやすい傾向があります。
- 例えば、芸能人のアカウントはフォロワーが増えやすいですね。
-
極端な差が生まれる(べき乗則)
- 結果として、少数の「超人気者」と大多数の「一般的なユーザー」が生まれます。
- 友達数100人以上の人は少なく、10人以下の人が多い、といった具合です。
なぜ重要なの?
このモデルは、SNSだけでなく、ウェブサイトのリンク関係、論文の引用ネットワーク、さらには都市間の航空路線網など、様々な現実世界のネットワークの特徴をうまく説明できます。
つまり、一見複雑に見える多くのネットワークが、実はシンプルなルール(新規参加と人気者効果)で形成される可能性があるのです。
Pythonでの実装
NetworkXライブラリを使えば、このモデルを簡単に実装できます:
import networkx as nx
# 1000ノード、各ノードは2本のエッジを持つネットワークを生成
G = nx.barabasi_albert_graph(n=1000, m=2)
このコードで生成されるネットワークは、現実世界の多くのネットワークと似た特徴を持っています。
3. グラフの基本統計を瞬時に計算
NetworkXを使えば、大規模グラフの基本的な統計情報を簡単に計算できます。
import networkx as nx
G = nx.barabasi_albert_graph(n=100000, m=2)
# 平均次数
avg_degree = 2 * G.number_of_edges() / G.number_of_nodes()
# クラスタリング係数
clustering_coeff = nx.average_clustering(G)
print(f"平均次数: {avg_degree:.2f}")
print(f"平均クラスタリング係数: {clustering_coeff:.4f}")
注意: 平均最短経路長の計算は大規模グラフでは時間がかかるため、ここでは省略しています。
出力例:
平均次数: 4.00
平均クラスタリング係数: 0.0008
4. 中心性指標で重要なノードを特定する方法
グラフ内で重要なノードを特定するには、中心性指標が有用です。ここでは、度数中心性を計算する方法を紹介します。
import networkx as nx
from collections import Counter
G = nx.barabasi_albert_graph(n=100000, m=2)
# 度数中心性の計算
degree_centrality = nx.degree_centrality(G)
# 上位10ノードを抽出
top_10_nodes = Counter(degree_centrality).most_common(10)
print("度数中心性が高い上位10ノード:")
for node, centrality in top_10_nodes:
print(f"ノード {node}: 中心性 {centrality:.4f}")
出力例:
度数中心性が高い上位10ノード:
ノード 0: 中心性 0.0076
ノード 8: 中心性 0.0065
ノード 9: 中心性 0.0065
ノード 1: 中心性 0.0059
ノード 5: 中心性 0.0053
ノード 58: 中心性 0.0034
ノード 6: 中心性 0.0029
ノード 23: 中心性 0.0029
ノード 18: 中心性 0.0026
ノード 34: 中心性 0.0025
5. 大規模グラフの可視化テクニック
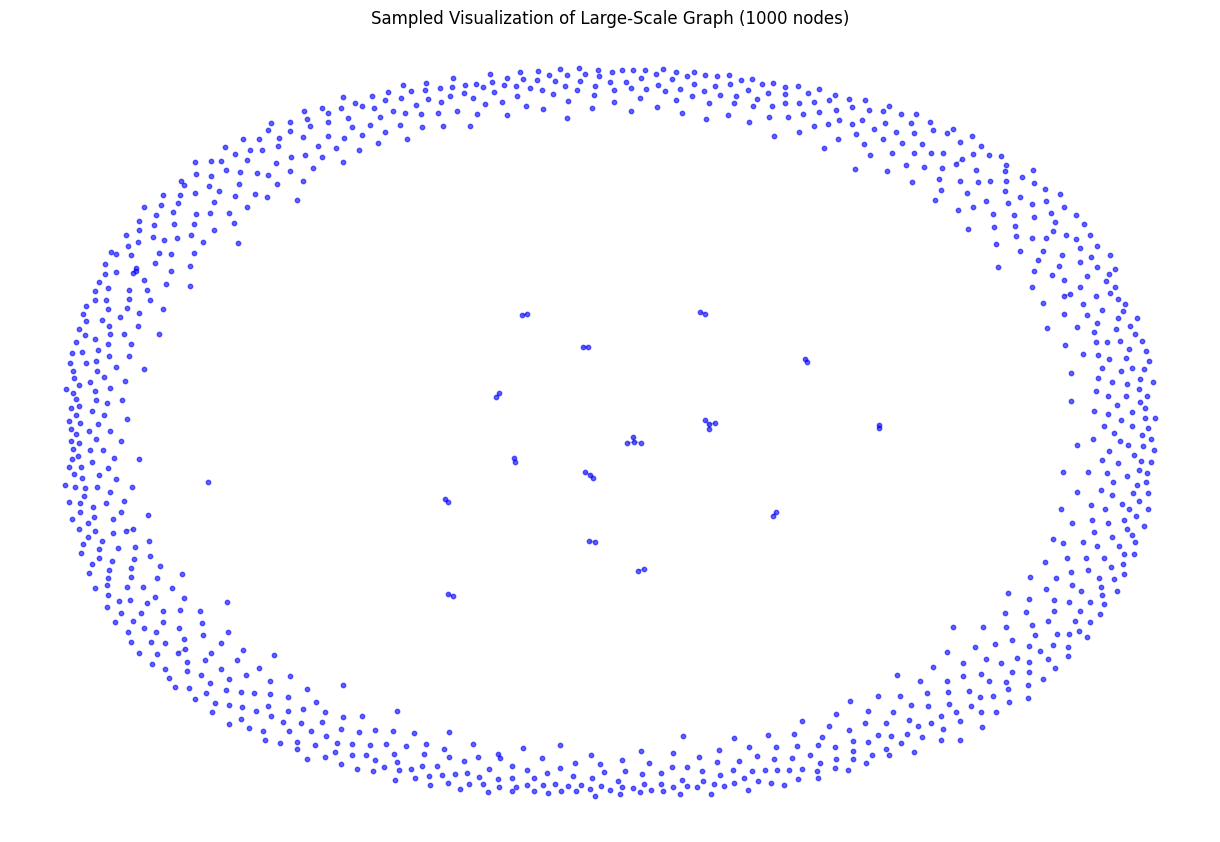
大規模グラフの可視化は難しい場合がありますが、サンプリングを使用することで効果的に可視化できます。以下のコードでは、10万ノードのグラフから1000ノードをランダムに選択し、そのサブグラフを可視化します。
import networkx as nx
import matplotlib.pyplot as plt
import random
# Generate a graph with 100,000 nodes
G = nx.barabasi_albert_graph(n=100000, m=2)
# Sample 1000 nodes randomly from the graph
sampled_nodes = random.sample(list(G.nodes()), 1000)
H = G.subgraph(sampled_nodes)
# Visualize the sampled graph
pos = nx.spring_layout(H)
plt.figure(figsize=(12, 8))
nx.draw(H, pos, node_size=10, node_color='blue', edge_color='gray', alpha=0.6)
plt.title("Sampled Visualization of Large-Scale Graph (1000 nodes)")
plt.axis('off')
plt.tight_layout()
plt.show()
このコードでは、random.sample() 関数を使用して、グラフのノードからランダムに1000個を選択しています。これにより、大規模グラフの構造を損なうことなく、管理可能なサイズのサブグラフを作成し、可視化することができます。
実行すると、Barabási-Albertモデルの特徴である、少数の高次数ノードと多数の低次数ノードが存在する構造を確認できるはずです。
注意点:
- 大規模グラフの一部を可視化しているため、全体の構造を完全に反映しているわけではありません。
- サンプリングの方法によっては、元のグラフの特性が失われる可能性があります。
- 可視化の結果は、サンプリングのランダム性により毎回異なります。
まとめ
本記事では、PythonとNetworkXを使って大規模グラフ処理を始める方法を5つのステップで解説しました。これらの技術を使えば、複雑なネットワーク分析や大規模データの処理が可能になります。
次のステップとして、以下のような発展的なトピックにチャレンジしてみてはいかがでしょうか:
- コミュニティ検出アルゴリズムの実装
- 時系列グラフ分析
- グラフニューラルネットワークの基礎
Pythonとグラフ理論の組み合わせは、データサイエンスの世界で大きな可能性を秘めています。ぜひ、本記事を参考に実践してみてください!
参考文献
- NetworkX公式ドキュメント: https://networkx.org/