はじめに
今回は画像処理についての内容になります。
画像処理技術というのは皆さん(エンジニアも含め一般の人も)が普段使用している技術
の一つになります。おそらく意識はしていないと思いますがとても身近です。
例えば、スマホの画像加工アプリ、インスタグラム、スマホ標準のカメラアプリなどは全て何らかの画像処理がされています。
今回はこのとても身近な技術について説明していきます。
※自分の勉強も兼ねています
今回はカラー画像についての説明はしません。説明すると量が多くなるため。
画像とは
そもそも画像とは何か?という説明から。
画像とは簡単に表すと数字の集まりです。
ん?どういうこと?と思われた方もいると思いますので画像を使って説明していきます。
ではまず画像の概念を説明していきます。
まず上記画像をズームしてみると以下のように見えます。

正方形がたくさんありますね。この1つが画素という単位になります。
この画素が集まって、画像になっています。
よく4Kとか耳にしたりすると思いますが、あれは横の画素が4000個程集まっているものを指します。
一般的な4Kのサイズとして以下になります。
3840 × 2160
これは横が3840個の画素で、縦が2160個の画素を表しています。
補足
解像度ってどういう意味?
よくこの言葉を耳にすると思いますが、これは画像や画面がどれだけ細かく情報
を表現できるかを示す指標になります。
解像度が高いと言えば画像、ディスプレイの面積あたりの画素数が多いことで、
解像度が低いと言えば画像、ディスプレイの面積あたりの画素数が少ないことになります。
次に、この1画素毎に注目すると画素の色が沢山ありますよね。
黒色だったり白色、グレーだったりと。この色こそが先ほど述べた数字になります。
色の階調を数字で表しているということになります。
一般的には0〜255(1Byte)の256段階の表現になります。
真っ黒が0で真っ白が255、その間がグラデーションになります。

補足
この数字は何を表しているのか。感のいい方は気づいたと思いますが、
これは明るさを表しています。”輝度値”、”光量”とも言います。
先ほどの画像の中身を見ると以下のようになっています。

ちなみにこの画像のことをグレースケール画像と言います。
モノクロ画像じゃないの?と思った方はいると思います。
グレースケール画像とモノクロ画像の違いは以下になります。
- グレースケール画像:0〜255の256階調で表現する画像
- モノクロ画像:0と1の2階調で表現する画像
簡単ですが、これで画像とはなにかのイメージはついたかと思います。
では次は実際に画像処理をしていきましょう。
説明する言語はC/C++で書いていきます。
OpenCVを画像の読み込み書き込み、ヒストグラムで使用していますが、
実際の画像処理には使用していません。
OpenCVを使用すると画像処理のアルゴリズムがわからないので。
動作環境
PC : M4 Macbook Pro(Sequoia 15.1)
コンパイラ : g++
c++ : 17
OpenCV : 4.10.0_*
エディタ:VScode
ソースコード
全体のソースコードは以下に格納しています。
画像処理(濃淡変換)
今回は基本である各画素に対しての処理を行います。
まず、画像処理なしだと以下の式が成り立ちます。
つまり入力画像がそのまま出力画像として出てきます。
$$P_o=P_i$$
$$P_iは入力画素、P_oは出力画素$$
では、これをベースに色々やっていきましょう。
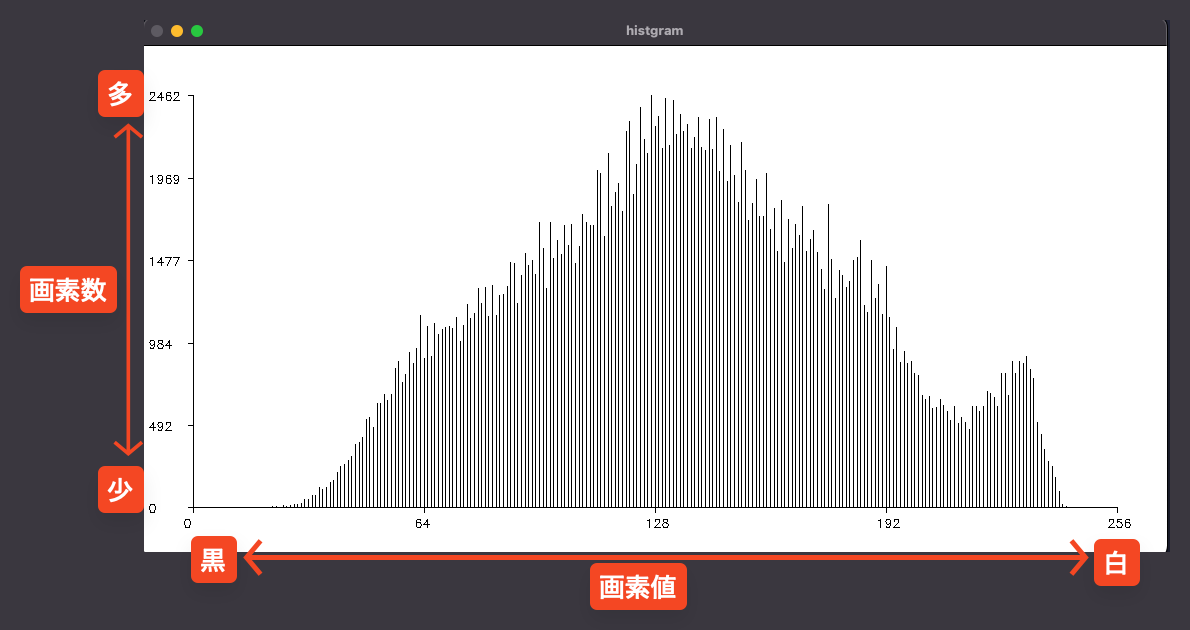
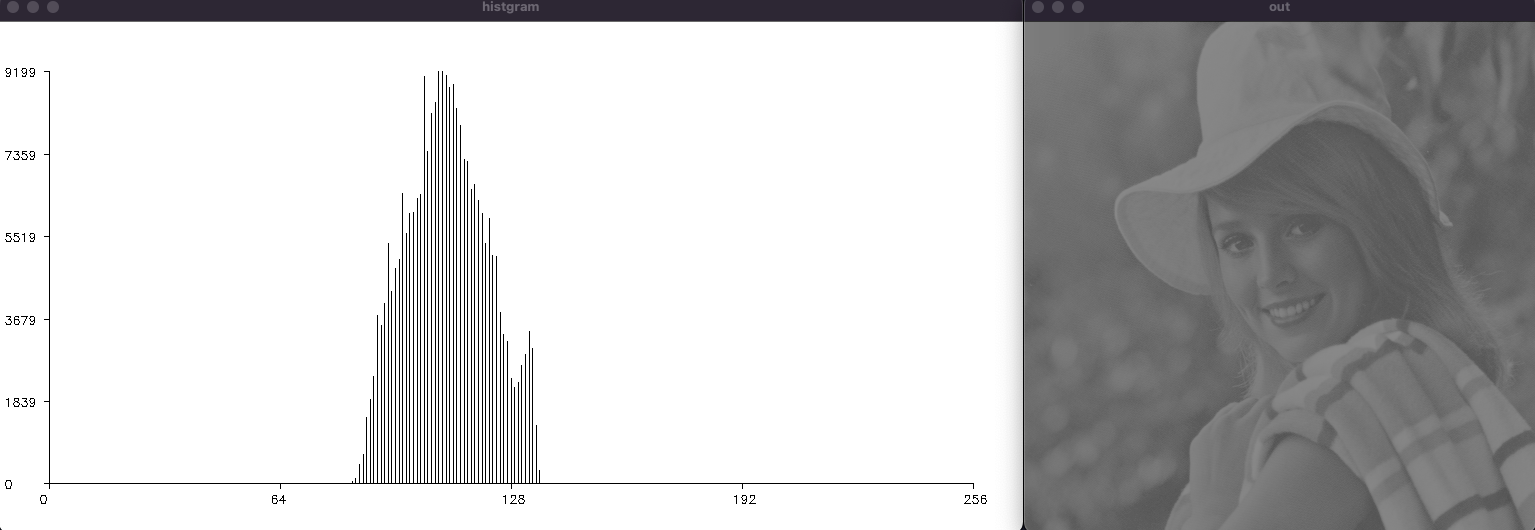
そのまえに今回使用する画像とヒストグラムは以下になります。
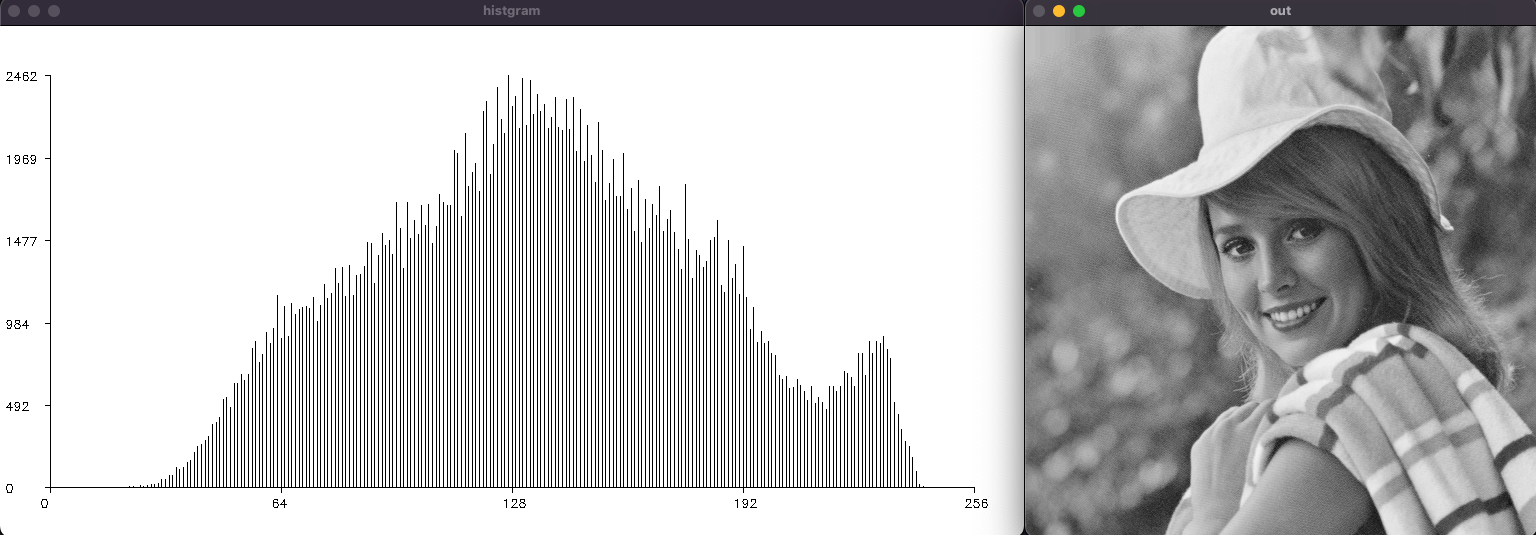
単調増加
単調増加のトーンカーブ処理になります。
$$P_o=P_i*coeff$$
$$P_iは入力画素、P_oは出力画素、coeffはスカラー係数$$
式はほぼ先ほどのものと同じです。係数が加わっただけです。
係数を2倍にすると出力も2倍に、3倍にすると3倍に、 0.5倍にしても入力と出力の関係は保たれるため単調増加となります。
ソースコード
void ImageProcessor::toneCurve(Mat inImg, int32_t height, int32_t width, double coeff, Mat outImg)
{
for (int32_t y = 0; y < height; y++) {
for (int32_t x = 0; x < width; x++) {
// 画素値を取得
Vec3b &pix = inImg.at<Vec3b>(y, x);
// 画素値を係数倍して範囲を0-255に収める
uint8_t blue = static_cast<uint8_t>(std::min(255.0, std::max(0.0, pix[BLUE] * coeff)));
uint8_t green = static_cast<uint8_t>(std::min(255.0, std::max(0.0, pix[GREEN] * coeff)));
uint8_t red = static_cast<uint8_t>(std::min(255.0, std::max(0.0, pix[RED] * coeff)));
// 画素値を設定
outImg.at<Vec3b>(y, x) = Vec3b(blue, green, red);
}
}
}
coeff=2
2倍にすると大多数が255(最大値)に張り付きます ※飽和対策のためクリッピングしています
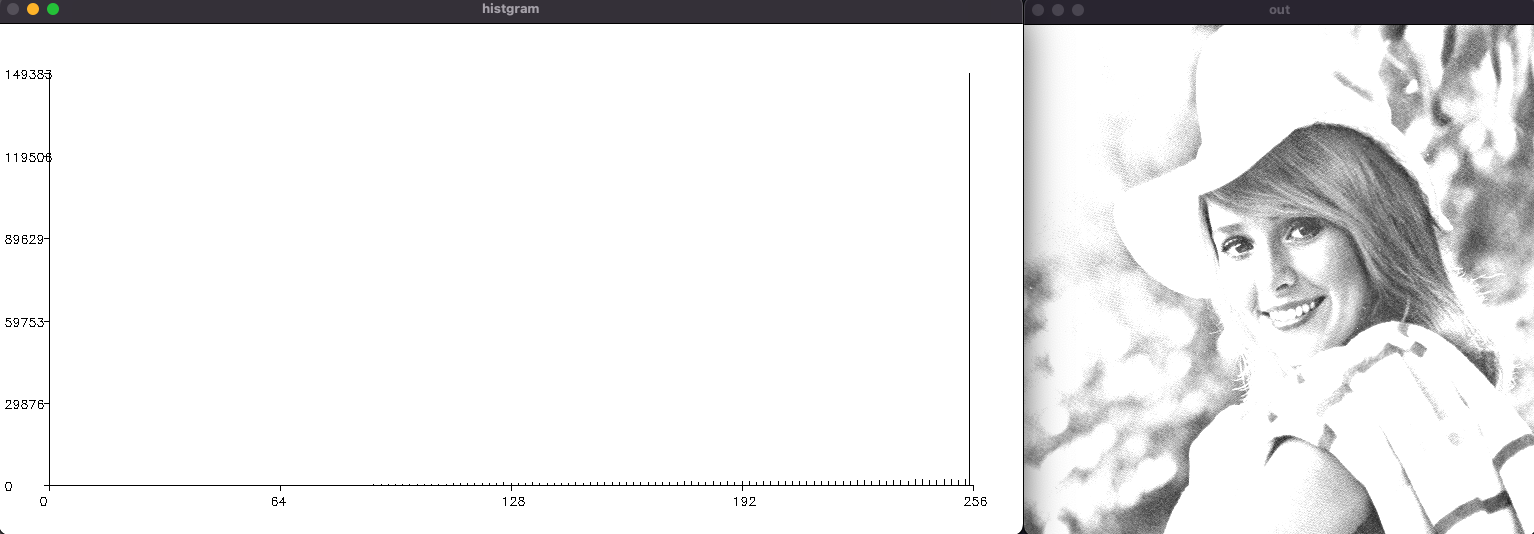
線形関数
線形関数処理になります。
$$P_o=aP_i+b$$
$$P_iは入力画素、P_oは出力画素、a,bは係数$$
この処理を施すとどうなるかですが、「明るい部分はより明るく」「暗い部分はより暗く」
コントラストを強調した画像を生成できます。
係数の役割
→aはコントラストの調整
→bは画像の明るさを調整
ソースコード
void ImageProcessor::effectLinear(Mat inImg, int32_t height, int32_t width, double a, double b, Mat outImg)
{
for (int32_t y = 0; y < height; y++) {
for (int32_t x = 0; x < width; x++) {
// 画素値を取得
Vec3b &pix = inImg.at<Vec3b>(y, x);
// 画素値を線形変換して範囲を0-255に収める
uint8_t blue = static_cast<uint8_t>(std::min(255.0, std::max(0.0, a * pix[BLUE] + b)));
uint8_t green = static_cast<uint8_t>(std::min(255.0, std::max(0.0, a * pix[GREEN] + b)));
uint8_t red = static_cast<uint8_t>(std::min(255.0, std::max(0.0, a * pix[RED] + b)));
// 画素値を設定
outImg.at<Vec3b>(y, x) = Vec3b(blue, green, red);
}
}
}
コントラスト比を上げつつ、画像全体を暗くした画像 a=1.5、b=-50

コントラスト比を下げつつ、画像全体を明るくした画像 a=0.7、b=50

そもそもコントラストと画像の明るさはどう違うのか?ですが、以下に例をあげます。
コントラストを上げたものと明るさを上げた画像を比較したいと思います。
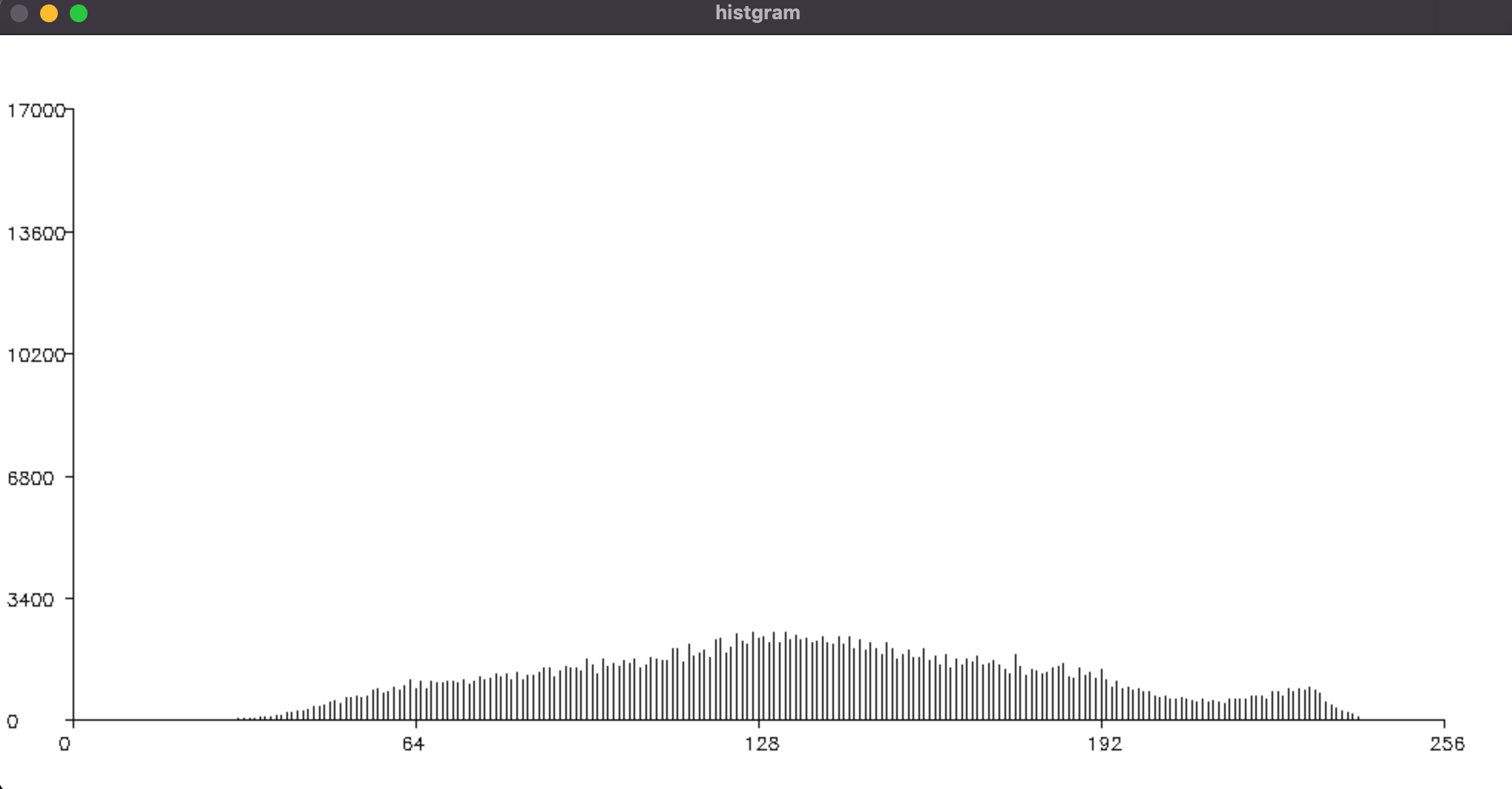
X軸の幅が広がる=明るい部分と暗い部分の差が広がったということになります。
次に画像の明るさのみ上げた例です。
対して画像の明るさのみを上げた画像ではX軸の幅は元のヒストグラムと同じになります。
ではなにが変わったかと言うと、全体的に画素値が大きくなった変化になります。
純粋に全ての画素値に対して+50の値になったため、ヒストグラムとしては右にスライドしたイメージです。
ガンマ補正
ガンマ補正とは
画像処理におけるガンマ補正とは、明るい部分と暗い部分を維持してその中間の明るさを調整することです。
※元々は人間の視覚特性とディスプレイや映像信号の特性を調整するために使用するのが目的
$$P_o=255(\frac{P_i}{255})^γ$$
$$P_iは入力画素、P_oは出力画素、γはガンマ値$$
図で入力画素と出力画素の関係を示すと以下になります。
ではこの図のガンマ値を設定するとどうなるのかですが、以下になります。
| ガンマ値 | 出力画像 |
|---|---|
| 0.5 | 明るくなる |
| 1.0 | 変化なし |
| 2.0 | 暗くなる |
ソースコード
void ImageProcessor::effectGamma(Mat inImg, int32_t height, int32_t width, double gammaVal, Mat outImg)
{
uint8_t LUT[256]; // Look Up Table
// LUTを作成
for (int32_t i = 0; i < 256; i++) {
// 0~1に正規化
double tmp = i / 255.0;
// ガンマ変換
LUT[i] = static_cast<uint8_t>(std::pow(tmp, gammaVal) * 255.0);
}
for (int32_t y = 0; y < height; y++) {
for (int32_t x = 0; x < width; x++) {
// 画素値を取得
Vec3b &pix = inImg.at<Vec3b>(y, x);
// 画素値をガンマ変換して範囲を0-255に収める
uint8_t blue = LUT[pix[BLUE]];
uint8_t green = LUT[pix[GREEN]];
uint8_t red = LUT[pix[RED]];
// 画素値を設定
outImg.at<Vec3b>(y, x) = Vec3b(blue, green, red);
}
}
}
大して難しいことはやっていないですが、先ほどまでの単純計算ではなくなったため
ソースコードの説明をします。
まず、大きく分けると2個の処理をやっています。
- LUTの作成
- 各画素の処理
順に説明していきます。
1.LUTの作成
そもそもLUTとはなんじゃ?という話ですが、
これは「Look Up Table(ルックアップテーブル)」の略です。
何を格納しているかと言うと、
入力値に対するガンマ補正後の値を事前に計算して格納しているテーブルになります。
格納イメージは以下になります。
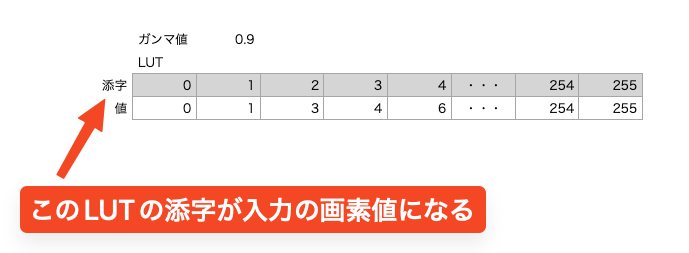
例えば、0の画素値が入力された場合の出力は0になり、4の画素値が入力された場合の出力は6になります。
なぜこのようなことをしているかと言うと、計算効率を良くし処理速度を上げるためです。
もちろん1画素ずつ計算することも可能ですが、毎回浮動小数点の計算、指数計算をするのは計算コストが高くなります。
計算量の違いを例に挙げます。
・直接計算の場合
計算時間=全画素数×浮動小数点、指数計算
・LUTの場合
計算時間=256回だけ(0〜255)
全体の画素数が少ないとまだマシですが、例えば解像度がフルHDの場合、1920×1080=200万回この計算をする必要出てきます。これでは非常にパフォーマンスが落ちてしまいます。
2.各画素の処理
こちらはすごく簡単で、先ほど作成したLUTに入力の画素値でアクセスし、値を取得&出力するだけです。
以下がガンマ補正をした画像になります。
シグモイド関数
どんな入力値でも 0から1の範囲に変換する特性を持っています。
入力の大きさが大きい値の場合、出力はほぼ1になり、小さい値の場合、出力はほぼ0になります。
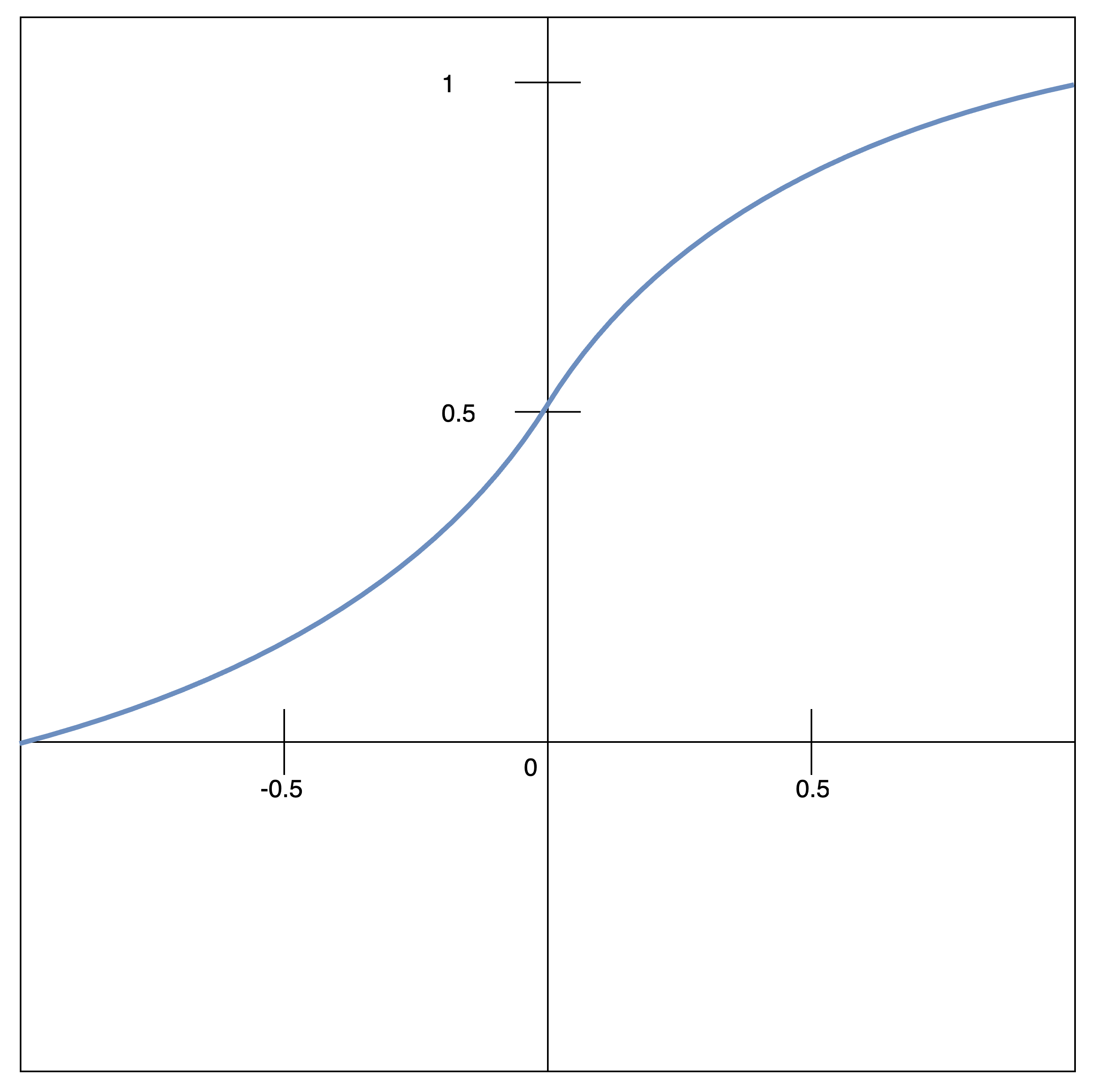
説明してもよくわからないと思いますので、以下に式と図を示します。
$$f(x)=\frac{1}{1+e^{-x}}$$
ただし、このままでは画像処理で使えないため少し式を変形させます。
$$P_o=\frac{1}{1+e^{-k({P_i-x_0})}}$$
$$P_iは入力画素、P_oは出力画素、kはシグモイドの傾き、x_0はシグモイドの中心位置$$
パラメータのkとx0についてもう少し説明します。
-
k
用途:傾きを調整する
イメージ:傾きが小さいと、画素値が徐々に変化する
画素値が大きいと、ある値を境に急激に明るくなったり暗くなったりする -
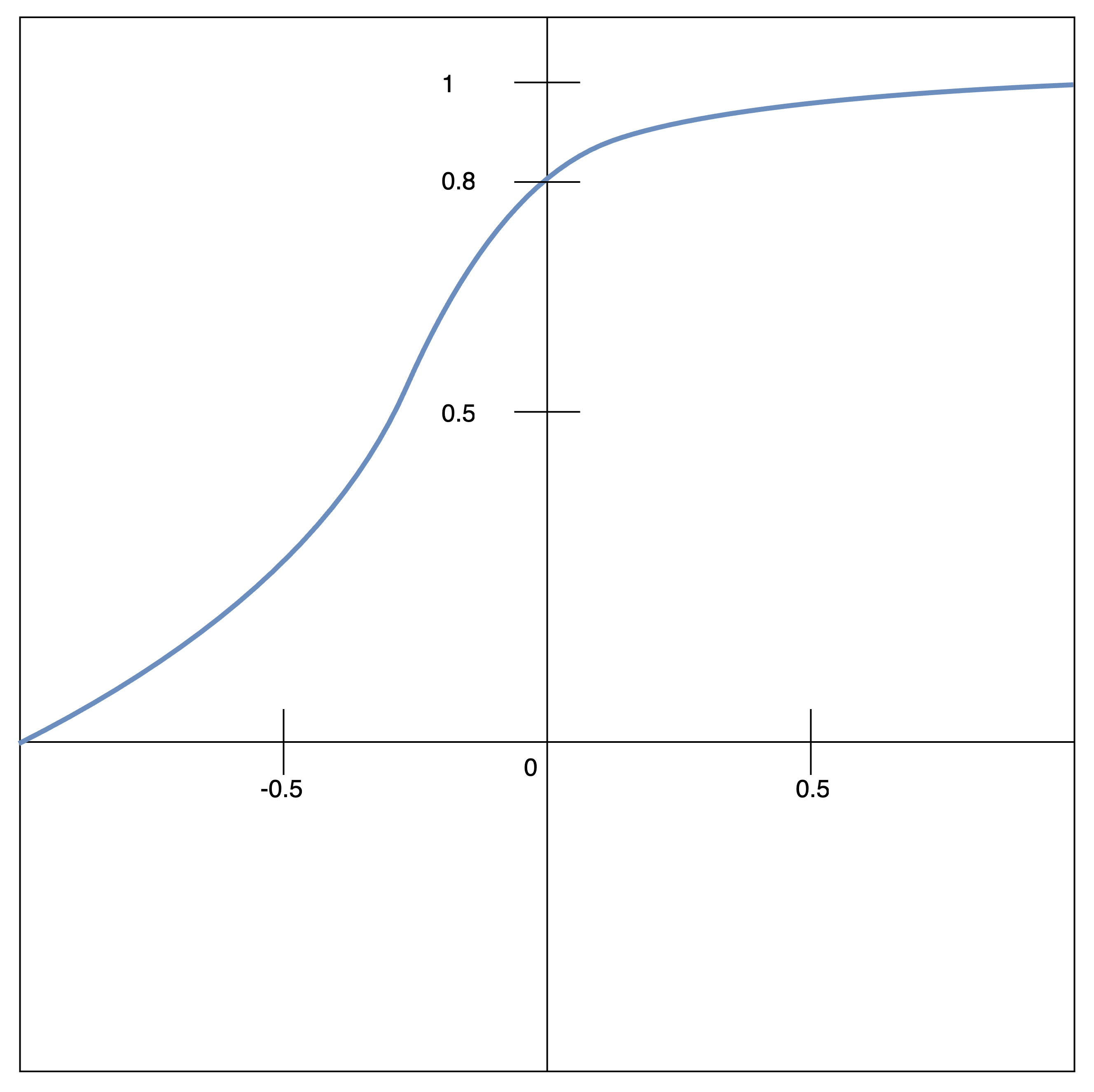
x0
用途:変化の中心点を調整する
イメージ:0.5を設定すると、画素値のちょうど中間点(127付近)で変化する
0.8を設定すると、画素値の明るい部分(204付近)で変化が強調される。
ソースコード
void ImageProcessor::effectSigmoid(Mat inImg, int32_t height, int32_t width, double k, double x0, Mat outImg)
{
uint8_t LUT[256]; // Look Up Table
// LUTを作成
for (int32_t i = 0; i < 256; i++) {
// 0~1に正規化
double norm = i / 255.0;
// シグモイド関数を適用
LUT[i] = static_cast<uint8_t>((1.0 / (1.0 + std::exp(-k * (norm - x0)))) * 255.0);
}
for (int32_t y = 0; y < height; y++) {
for (int32_t x = 0; x < width; x++) {
// 画素値を取得
Vec3b &pix = inImg.at<Vec3b>(y, x);
// 画素値をシグモイド関数で変換して範囲を0-255に収める
uint8_t blue = LUT[pix[BLUE]];
uint8_t green = LUT[pix[GREEN]];
uint8_t red = LUT[pix[RED]];
// 画素値を設定
outImg.at<Vec3b>(y, x) = Vec3b(blue, green, red);
}
}
}
先ほどのガンマ補正と同じく、事前に計算したシグモイドをLUTへ格納し使用しています。
以下がシグモイド関数を使用した画像になります。
ヒストグラム均等化
ヒストグラム均等化とは、画像のコントラストを強調するための画像処理になります。
色々やり方はあるそうなのですが、今回は累積分布関数(CDF)でやります。
まず、累積分布関数とはなにか?ですが、
ある値以下のデータが全体の中でどの程度の割合を占めるかを表したものです。
$$F(x)=P(X \leq x)$$
$$Xは確率変数(今回で言えば画像の画素値)、xはある値$$
ではこれをどのように適用するのかですが、以下の計算手順で求めていきます。
-
ヒストグラムを正規化する
ヒストグラムを全ピクセル数で割り、各画素値の頻度(確率)を計算する
$$正規化ヒストグラム:h(i)=\frac{ヒストグラムの値(画素値(i)の数)}{全ピクセル数}$$ -
累積頻度を計算する
各画素値iのCDFは、画素値0からiまでの正規化ヒストグラムの合計になる
$$F(i)=\sum_{j=0}^i h(j)$$
$$F(i)はi以下の画素が全体のどのくらいの割合を占めているか、h(j)は正規化された頻度$$
1の方は簡単にイメージできると思いますので、2の方を例にあげます。
↓例のヒストグラム
| 画素値 j | 正規化頻度 h(j) |
|---|---|
| 0 | 0.1 |
| 1 | 0.2 |
| 2 | 0.4 |
| 3 | 0.3 |
これを累積分布関数F(i)で計算すると以下になります。
・F(0) = h(0) = 0.1
・F(1) = h(0) + h(1) = 0.1 + 0.2 = 0.3
・F(2) = h(0) + h(1) + h(2) = 0.1 + 0.2 + 0.4 = 0.7
・F(3) = h(0) + h(1) + h(2) + h(3) = 0.1 + 0.2 + 0.4 + 0.3 = 1.0
結果の見方としては、以下のように捉えることができます。
F(i)=0.7の場合、i以下の画素が全体の70%を占める。
この情報を使用することにより、元のヒストグラムの頻度分布を累積割合に基づいて均等にスケーリングできます。
ちょっとごちゃごちゃしてわかりにくいですが、最後にこの計算式を順に適用していった例を示します。

この例はあくまで計算用なので値が極端ですが、計算の全体イメージはこんな感じです。
ソースコード
先ほどの説明とあわせて読んでみてください。
・1のヒストグラムの正規化処理
void ImageProcessor::calcNormHist(Mat inImg, int32_t height, int32_t width, float *hist)
{
int64_t histTmp[256] = {0};
int64_t sum = 0;
// ヒストグラムの作成(画像の全画素を走査)
for (int32_t y = 0; y < height; y++) {
for (int32_t x = 0; x < width; x++) {
// 画素値を取得
Vec3b &pix = inImg.at<Vec3b>(y, x);
// グレースケールなためどれか一つの値を取得
int32_t pixVal = pix[BLUE];
histTmp[pixVal] = histTmp[pixVal] + 1;
sum += 1;
}
}
// ヒストグラムの正規化
for (int32_t i = 0; i < 256; i++) {
hist[i] = static_cast<float>(histTmp[i]) / sum;
}
}
・2の累積頻度計算処理(全体)
void ImageProcessor::histEqualization(Mat inImg, int32_t height, int32_t width, Mat outImg)
{
float hist[256];
uint8_t histEq[256];
float sum;
// ヒストグラムの正規化
calcNormHist(inImg, height, width, hist);
// iの画素値までの累積分布関数を計算
for (int32_t i = 0; i < 256; i++) {
sum = 0.0;
// 0~iまでのヒストグラムの和を計算
for (int32_t j = 0; j <= i; j++) {
sum = sum + hist[j];
}
// ヒストグラムの累積分布関数を計算(0~255の範囲に正規化)
histEq[i] = static_cast<uint8_t>(255 * sum + 0.5);
}
// ヒストグラム均等化
for (int32_t y = 0; y < height; y++) {
for (int32_t x = 0; x < width; x++) {
// 画素値を取得
Vec3b &pix = inImg.at<Vec3b>(y, x);
// 画素値をヒストグラム均等化して範囲を0-255に収める
uint8_t blue = histEq[pix[BLUE]];
uint8_t green = histEq[pix[GREEN]];
uint8_t red = histEq[pix[RED]];
// 画素値を設定
outImg.at<Vec3b>(y, x) = Vec3b(blue, green, red);
}
}
}
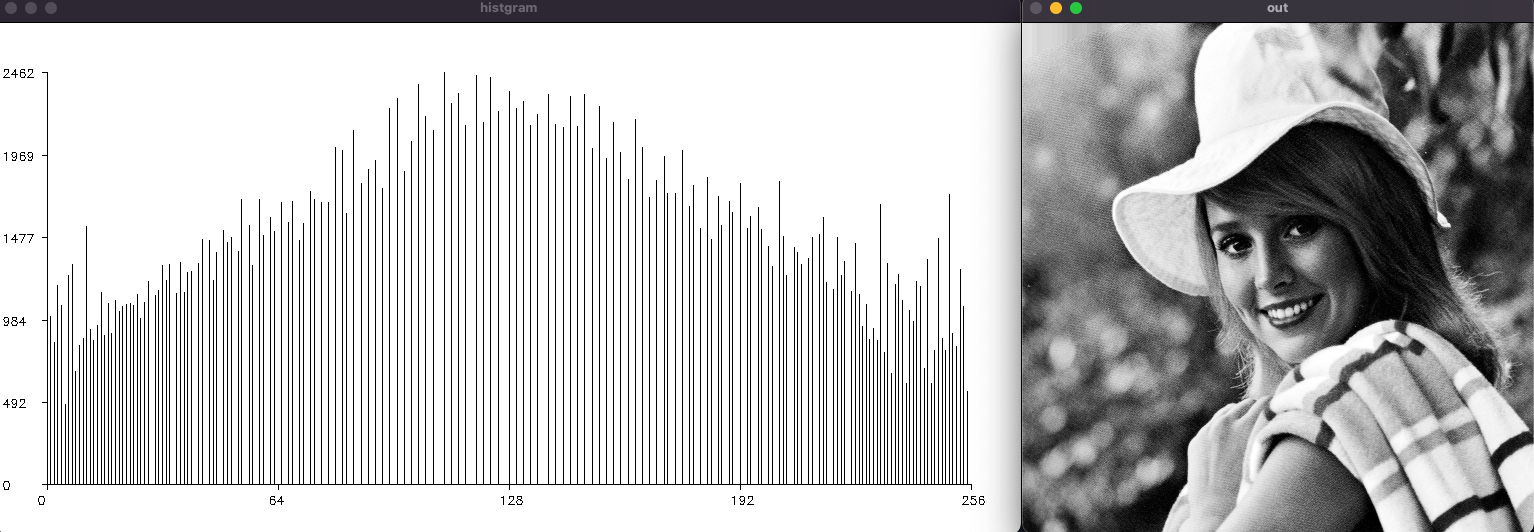
以下がヒストグラム均等化を使用した画像になります。
元画像と比べて全体的に画素値が散らばり、コントラストが強調され、
絵が綺麗になりましたね。
元の画像も改めて載せておきます。
ネガ処理
最後にオマケでちょっと特殊な処理を紹介します。
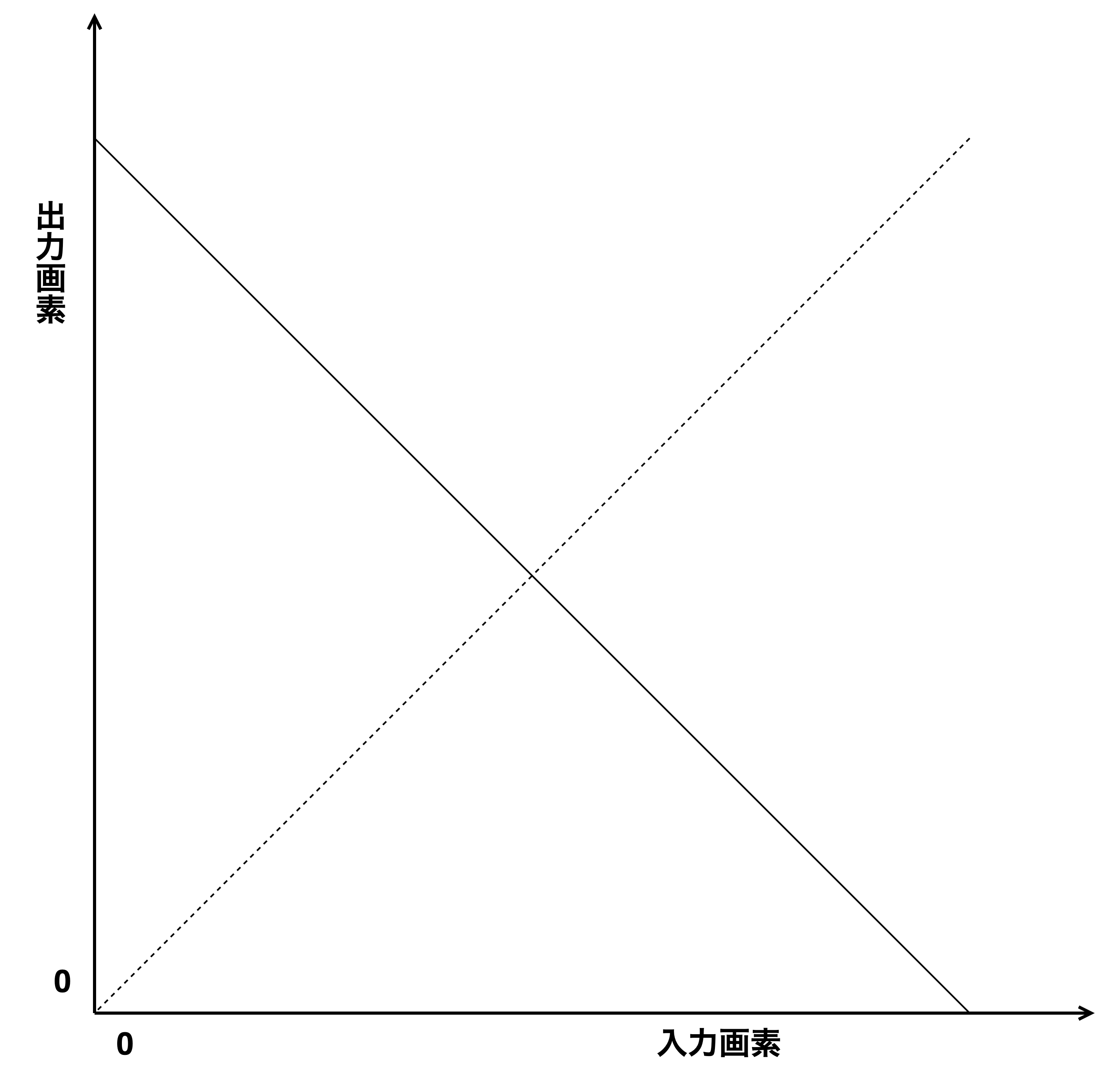
ネガ処理というもので、要は明暗を反転する処理になります。
$$P_o=255-P_i$$
$$P_iは入力画素、P_oは出力画素$$
ソースコード
void ImageProcessor::effectNega(Mat inImg, int32_t height, int32_t width, Mat outImg)
{
for (int32_t y = 0; y < height; y++) {
for (int32_t x = 0; x < width; x++) {
// 画素値を取得
Vec3b &pix = inImg.at<Vec3b>(y, x);
// 画素値を反転して範囲を0-255に収める
uint8_t blue = 255 - pix[BLUE];
uint8_t green = 255 - pix[GREEN];
uint8_t red = 255 - pix[RED];
// 画素値を設定
outImg.at<Vec3b>(y, x) = Vec3b(blue, green, red);
}
}
}
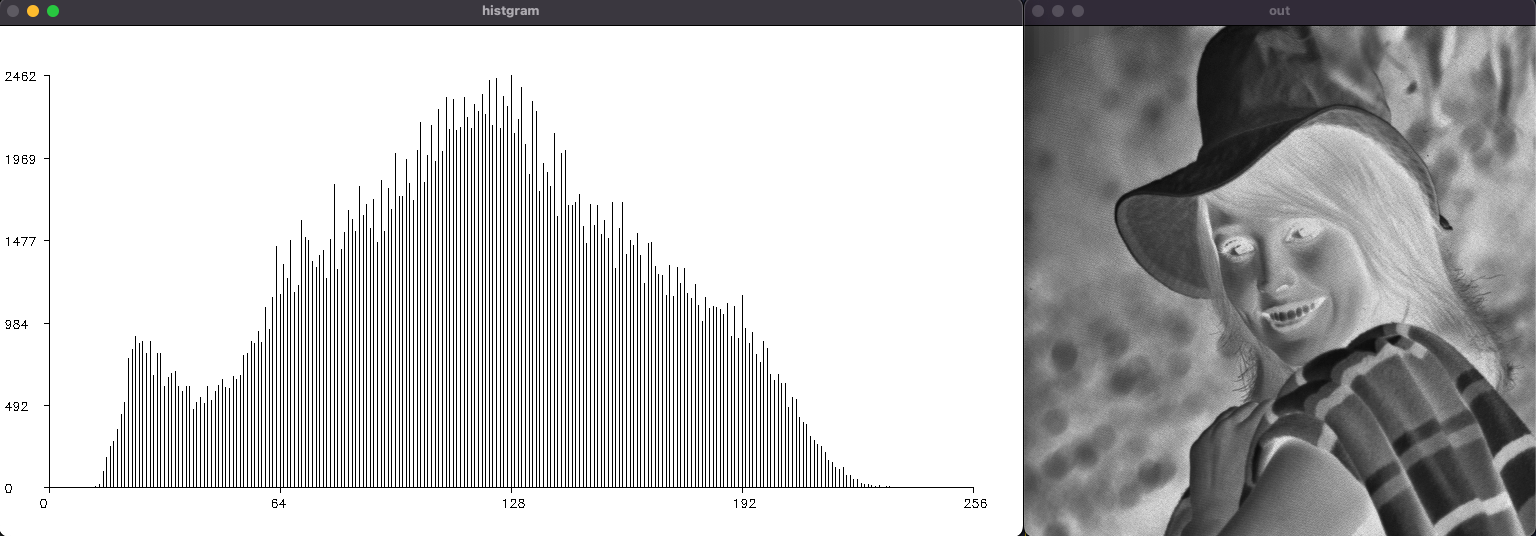
以下がネガ処理を使用した画像になります。
最後に
以上で各画素に対しての画像処理は終わりになります。
もっと他にも色々ありますが、やる気が出たらやるかもです。
でも次は他の画像処理(フィルタ)をやっていければと思います。