はじめに
半年ほど前からサウナにハマりました。
そして、年末年始に時間があったので、その期間を使って因果推論・因果探索を軽くお勉強していました。
というわけで、サウナを使って因果推論の基本となる部分を復習してみます。あくまで、自分の理解をサウナに置き換えるだけですが。
誤っている場合は、ズバズバと指摘していただけると、僕の勉強が捗るのですごく助かります。
お勉強に使用した書籍は、Pythonライブラリによる因果推論・因果探索[概念と実践] です。
書籍のアマゾンリンク貼っておきます。( https://amzn.asia/d/guOq7aT )
僕は完全に初学者でしたが、例が多くて非常に理解しやすく、章末ごとにまとめが書かれていることもあって読みやすかったです。
因果のはしご
はしごの1段目が関連、2段目が介入、3段目が反事実とされていて、低い段から登る過程において、より想像の世界が広がっているという認識です。
- 1段目「関連」 → サウナ中に計測できたデータを使って予測する
- 心拍数、体温、サウナ室の温湿度、サウナ利用時間を使って、ととのい具合を予測する
- 2段目「介入」 → サウナ中に計測できたデータの一部を変更する(=条件付けする)ことで、その他がどういう影響を受けるかを予測する
- あとサウナ室に2分多く入っていると、他のデータ(心拍数、体温など)はどうなるか、ととのい具合はどうなるか
- 3段目「反事実」 → 予想することすらできない状態(=妄想)
- OOっていうサウナでととのった!XXっていうサウナだったら、さらにととのったのかな?(同時に2つの事象を満たせない)
- サウナ室で突然倒れてしまった、そういえば水を全然飲んでなかったので、もし水を飲んでいたらどうなっただろう?(再現性がない)
関連 →[データを一部変えてみる]→ 介入 →[予想したデータを使って、さらに予想する]→ 反事実、というイメージです。
DAGとチェーン / フォーク / コライダー
因果推論を実施するにあたって、原因と結果をわかりやすくするためにグラフ因果モデルと呼ばれる、有向グラフを作ることになります。このときのグラフは特にDAG(非巡回有向グラフ)と呼ばれる構造でなければならず、簡単に言えば、グラフが巡回してはダメ(原因と結果がぐるぐる巡ってしまうので)で、かつ関係性がわかるように方向付き矢印によって結ばれている必要があります。
そのグラフの一部分を見ると、大きく3つに区別することができ、それがチェーン / フォーク / コライダーになります。
以下画像がチェーンと呼ばれる構造です。自身が受けた影響を踏まえて、他へ影響を与える役割になります。
このとき、「外気温」が自分にベストマッチしていたとしても、原因の大元である「外気浴」がそもそも施設になかったら意味ないですよね。というように、チェーンは無条件に従属な関係であると表現され、「外気温」を何かしら操作することで、大元である外気浴の有無を無視することになり、これを独立な関係と呼びます。

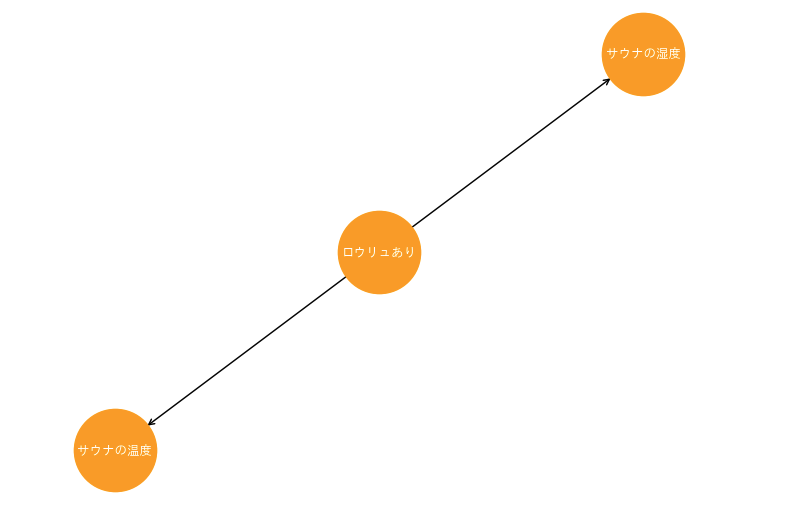
以下の画像がフォークです。自身の影響が複数に影響を与える状態です。
ロウリュが発生することによって、サウナ室内の温度と湿度が上昇することは容易に想像できると思います。このような、1つの変更が複数に影響を与えるとき、その根本となる要因を共通原因と呼びます。
そして、共通原因である「ロウリュあり」を変化させると、「サウナ室の温度」と「サウナ室の湿度」の関係は無関係になります。あくまで、「ロウリュあり」が変化していない状態においては、他の2つは関係性が間接的に結ばれていますが、共通原因が変化することによって、その先の原因同士が独立します。
すなわち、先ほどのチェーンと同様に、フォークも無条件に従属であり、共通原因を変化させることで独立の関係になります。
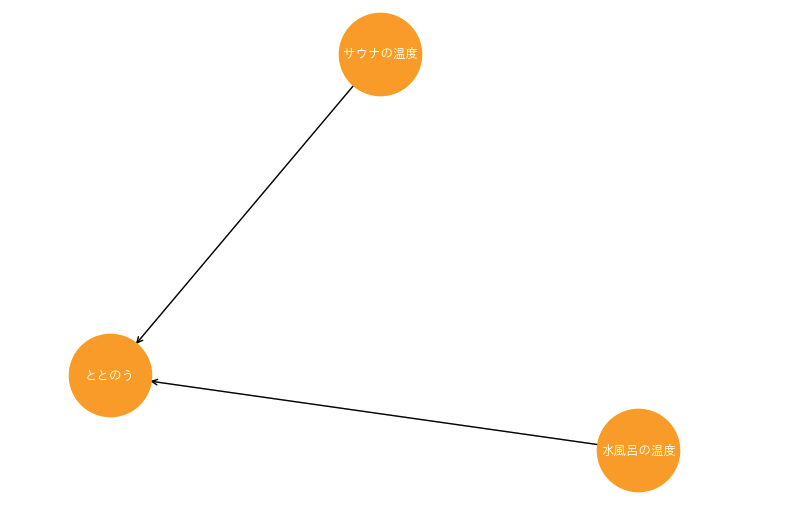
コライダーは、以下画像の構造です。複数の要因が1つに向かっている状態を指します。
このグラフは、「サウナ室の温度」と「水風呂の温度」がそれぞれ影響を与え合って、「ととのう」状態になることを意味しています。
先ほどのチェーンやフォークと異なり、コライダーは無条件に独立しています。「ととのう」という状態になるためには、他の影響を受ける必要があるためです。言い換えると、無条件でない(=変化させる)場面においては従属な関係になります。
まとめると、チェーンとフォークは無条件に従属な関係であり、コライダーは無条件に独立な関係になります。
この考え方を使ってグラフ因果モデルを観察することで、推論したい原因と結果の間に影響を与えてしまう不必要な要因を排除することができます(=d分離)。
A(原因)→B(結果)という因果を推論したいときに、全然関係ないCが影響を与えてしまうと、A→Bをうまく推論できなくなります。そのため、A→BのグラフからCを独立させる必要があります。
エスティマンドとバックドア基準 / フロントドア基準 / 操作変数法
エスティマンドとは、何を推定したいかという因果関係を指します。先ほどのDAGに話が戻りますが、これらで推定したい原因と結果のノードを選択し、その2つのノード間の過程のことを指します。このエスティマンドを見つけるために使われる手法として、バックドア基準 / フロントドア基準 / 操作変数法がよく挙げられます。
バックドア基準は、エスティマンドを見つけるために、目的の因果間に影響を与えてしまう別の原因のパスをブロックすることが目的であり、因果間が隣接している(=結果に対する直接的な原因である)必要があります。ここでいうブロックするとは、先ほどのチェーン / フォーク / コライダーの構造でいう因果的な独立関係になっていることを指します。
以下のグラフモデルがあったと仮定し、「外気温」→「ととのう」をエスティマンドだとすると、「外気浴あり」→「ととのう」という過程によって「ととのう」が影響を受けてしまうため、純粋な「外気浴」→「ととのう」という因果関係を推定できなくなってしまいます。このような場面にて、「外気浴あり」というノードはフォークであるため、このノードをコントロールすることで独立な関係になり、「外気温」→「ととのう」という因果関係が純粋に推定できることになります。
書籍でも述べられていましたが、あくまで理想的なグラフモデルではバックドア基準が使えますが、現実においてはこれら以上に様々な要因が絡み合っているため、そううまくバックドア基準を満たせることはほぼないらしいです(そもそも隠れ交路を完全に排除することが困難)。
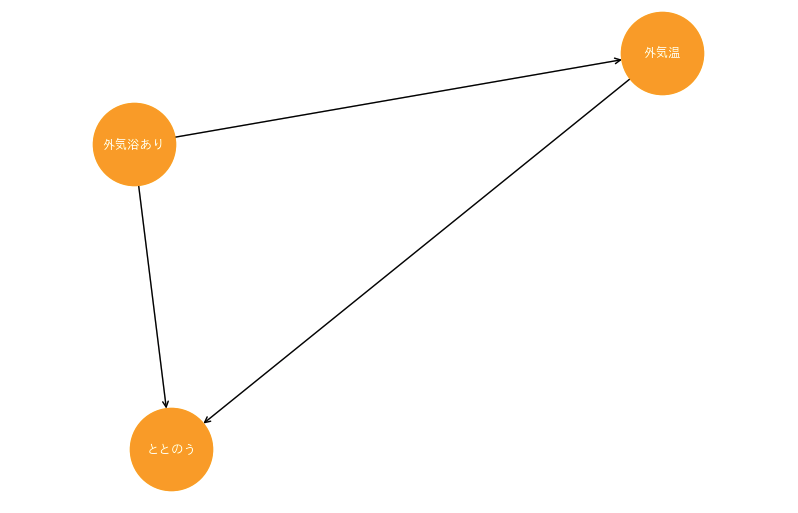
フロントドア基準は、先ほどのバックドア基準のように、エスティマンドが隣接していない場面で使用される手法です。以下のグラフモデルにおいて、「外気浴あり」→「ととのう」というエスティマンドを仮定したとき、この因果間に「外気温」というノードが存在することで、バックドア基準が適用できません。この因果間の中間に位置するノードを、媒介変数などと呼ぶそうです。
この媒介変数を見つけることで、間接的に因果を推定することが可能になり、このときフロントドア基準が満たされます。

操作変数法は、推定したい因果間に影響を及ぼす他の原因があると知っているものの、それが観測できない場面で使われる手法です。
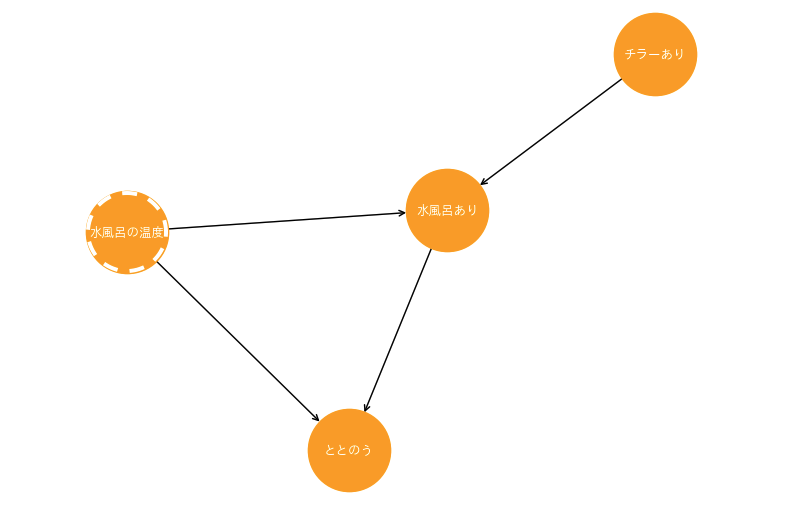
以下のグラフモデルにおいて、エスティマンドは「水風呂あり」→「ととのう」だとします。このとき、「ととのう」には「水風呂の温度」も影響を及ぼすということは把握していますが、そのデータを観測できない場合を想定します(観測できないノードは点線で囲んだ)。こういう場面で操作変数法を使い、「水風呂あり」に影響を与える「チラーあり」というノードをコントロールさせます。この「チラーあり」というノードの変化は、「水風呂あり」に影響を与える一方で、「水風呂の温度」に直接的に影響を与えないということが可能です。それによって、「水風呂あり」→「ととのう」という因果効果を測ることが可能になります。
ただし、操作変数法は、3つのルールが守られている場合に限って使用可能です。
- 操作変数と原因ノードが隣接している
- 「チラーあり」と「水風呂あり」が隣接している
- 操作変数と結果ノードに共通の原因がない
- 「チラーあり」と「ととのう」のノードに対して、共通のノードがない
- 操作変数から影響を受けるノードは、その他に影響を与えない
まとめると、バックドア基準 →[測定したい因果間が隣接していない]→ フロンドドア基準 →[媒介変数が観測できない]→ 操作変数法という順番で、エスティマンドを見つける流れです。グラフモデル次第では、操作変数法→フロントドア基準にもなります。
このあたりのエスティマンドを見つける作業は、Pythonだとdowhyライブラリを使って色々とやってくれます。
おわりに
書籍では、全体の約半分くらい、こういった基礎的な内容がぎっしりと書かれており、初学者でも本当に読みやすかったです。これらを踏まえて、後半ではライブラリをつかって因果推論・因果探索を実装したので、後半はすごく手応えがありました。
時間を取れる機会があったら、次は自分なりにサウナに関するグラフモデルを構築してみて、実際に因果推論してみたいと思っています。