先日Atcoder Beginner Contest 141に参加してきたが、D問題がいくらやってもTLEになり詰まった挙句TIME UPになった。
原因はリストから最大値を取り出してくる箇所で、リストから最大値を取り出し、2で割って(点以下切り捨て)再度リストに格納、という動作をループで回す必要があったのだが、いくら直してもTLEになり続けた。
自分が考えていた方法としては
- リストの最大値を取る組み込み関数 max() を使う
- リストをソート ( sort() ) して一番後のインデックスにある要素(=最大値)を取る
だったのだが、いずれの場合も時間がかかってしまうらしい。
どのようにすれば良かったのか・・?
解説を見て学んだのが "優先度付きキュー" というアルゴリズム。
この優先度付きキューについて、調べて見た。
優先度付きキュー
優先度付きキュー (Priority Queue) とは以下の操作が行えるデータ構造。
- キューに数(要素)を優先度付きで追加する。
- 最も高い優先度を持つ要素を取り出す(値を取得し、削除する)
これを二分木(ヒープ)を用いて効率的に実現したデータ構造の事を言う。
ヒープの特性上、優先度付きキューにおいて最も高い優先度を持つ要素とは最小値のことになり、
優先度付きキューとは最小値を取り出す事の出来るデータ構造と言うことになる。
ヒープとは
ではヒープ(二分木)とは何か?
ヒープとは、「子要素は親要素より常に大きいか等しい(または常に小さいか等しい)」と言う制約を持つ木構造の事。単に「ヒープ」という場合、二分木を使った二分ヒープを指すことが多いため、そちらを参照すること。
ヒープは最小値(または最大値)を求めるのに適した木構造の一種であり、「子要素は親要素より常に大きいか等しい(または常に小さいか等しい)」と言う制約を持つ。子要素が複数ある場合、子要素間の大小関係に制約はない。
(Wikipediaより)
図に表すと以下のような構造を持つデータ構造である。
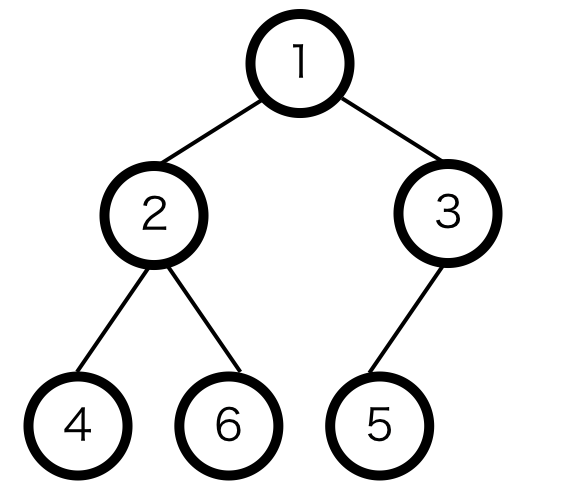
図にある通り、ヒープの特徴としては「子要素は親要素より常に大きいか等しい」と言うところである。
また、ヒープは上から下へ、左から右へ順にノードが詰まっていく。
「子要素は親要素より常に大きいか等しい」と言う定義から、ヒープの一番親の要素(根)は、ヒープで一番小さい値(最小値)ということになる。
データの挿入
ヒープにデータを挿入すると、入力したデータはまずヒープの最後尾に追加され、親要素と大小を比較し、親要素よりも大きくなるまで上に上げていく。(下図)

データの削除
ヒープからデータを削除(=最小値を削除)した時は、根の位置に最後尾の要素を持っていき、その後子要素と大小を比較していずれの子要素よりも小さくなるまで下に下げていく。(下図)

Pythonでの優先度付きキュー
ではこのヒープ及び優先度付きキューをプログラミングで実装するにはどうすれば良いのか?
今回も私が現在競プロでよく使用しているPythonで考えてみることにした。
しかし、調べてみると何と優先度付きキューもPythonではライブラリが実装されているそうだ。
それがこの heapq と言うライブラリで、このライブラリについて調べて見た。
heapq
heapqライブラリの諸関数を以下に記載する。
heapify
heapify関数はリストをヒープに変換する関数である。
>>> import heapq
>>> a = [7,5,3,2,4,8,10,1]
>>>
>>> a
[7, 5, 3, 2, 4, 8, 10, 1]
>>>
>>> heapq.heapify(a)
>>>
>>> a
[1, 2, 3, 5, 4, 8, 10, 7]
変換し作成されたヒープはリストを使って表現される。
このリストでのヒープの見方は、リストのインデックスをkとした時、
- 親要素 : リスト[k]
- 子要素 : リスト[2k+1]、リスト[2k+2]
となる。
heappush,heappop
heappush関数は要素をヒープにpushする関数である。
pushされた要素は前述のヒープ挿入例に基づき、ヒープ内で要素が移動され、最終的にヒープ内で親子間の大小が保たれた形で保持される。
対して、heappop関数はヒープから要素を取り出し取得する関数である。
なお、heappopで取り出すのはヒープにおける最小の要素である。
heappop後のヒープはheappushの時と同様に前述のヒープ削除例に基づき、ヒープ内で要素が移動され、最終的にヒープ内で親子間の大小が保たれた形で保持される。
使用例を以下に示す。
>>>
>>> import heapq
>>> a=[5,3,2,1,6,13,4,12,14,9,10]
>>> heapq.heapify(a)
>>>
>>> a
[1, 3, 2, 5, 6, 13, 4, 12, 14, 9, 10]
>>>
>>> heapq.heappush(a,7) #7をヒープにプッシュ
>>>
>>> a
[1, 3, 2, 5, 6, 7, 4, 12, 14, 9, 10, 13]
>>>
>>> heapq.heappop(a) #ヒープから要素をpop
1
>>> #最小の要素(1)がヒープからpopされる
>>>
>>> a
[2, 3, 4, 5, 6, 7, 13, 12, 14, 9, 10]
>>>
heappushpop,heapreplace
heappushpop関数はheappushとheappopを同時に行う関数である。
順序としてはheappushを行ってからheappopを行う。
heapreplace関数はその逆でheappopとheappushを同時に行うと言う点では同じだが、
順序はheappopを行ってからheappushを行う。
公式によるとheappushとheappopを別々に行うよりも、これらの関数を使う方が効率的に行えるとの事。
使用例を以下に示す。
>>> import heapq
>>> a=[5,3,2,1,6,13,4,12,14,9,10]
>>> heapq.heapify(a)
>>>
>>>
>>> a
[1, 3, 2, 5, 6, 13, 4, 12, 14, 9, 10]
>>>
>>>
>>> heapq.heappushpop(a,11)
1
>>>
>>> a
[2, 3, 4, 5, 6, 13, 11, 12, 14, 9, 10]
>>>
>>> heapq.heappushpop(a,1)
1
>>>
>>> a
[2, 3, 4, 5, 6, 13, 11, 12, 14, 9, 10]
>>>
>>> heapq.heapreplace(a,7)
2
>>>
>>> a
[3, 5, 4, 7, 6, 13, 11, 12, 14, 9, 10]
>>>
>>> heapq.heapreplace(a,1)
3
>>>
>>> a
[1, 5, 4, 7, 6, 13, 11, 12, 14, 9, 10]
>>>
heappushpop,heapreplaceはpushとpopを行う順序から、popした時に取り出される要素は最小の要素でない場合もあると言うことに注意する。
上記の例でいうと、ヒープにヒープのどの要素よりも小さい要素をpushした時、heappushpopの場合は要素をpushしてからpopするためpushした要素がpopされるが、
heapreplaceはヒープからpopしてから要素をpushするため、popされる要素はpushする前のヒープの最小値であり、また動作後のヒープはpushした要素が最小値となったヒープになる。
ヒープから最大値を取り出すには?
ヒープはその特性上、最小値しか取り出すことはできない。
もし、最大値を取り出したいといった時はどうするか?
方法の一例としては、要素の符号を全て逆転(-1を掛ける)させてからヒープを組ませる。
すると、そのヒープの最小値には元の最大値×(-1)した要素が来る。
その要素を取り出して(pop)また符号を逆転(-1を掛ける)させてやれば、最終的には最大値を取り出すことが可能となる。
>>> import heapq
>>> #リスト(ヒープ)aから最大値を取り出す。最大値は14
>>> a=[5,3,2,1,6,13,4,12,14,9,10]
>>>
>>> #要素に全て-1をかけて符号を逆転する
>>> a=[-1 * i for i in a]
>>> a
[-5, -3, -2, -1, -6, -13, -4, -12, -14, -9, -10]
>>>
>>> heapq.heapify(a)
>>> a
[-14, -12, -13, -5, -10, -2, -4, -3, -1, -9, -6]
>>> #元の最大値×(-1)させた-14がヒープの最小値に来る
>>>
>>> #ヒープから最小値を取り出し-1を掛ける
>>> heapq.heappop(a) * -1
14
>>> #元の最大値14が取り出された
今後活用する機会があれば利用していきたい。