テクスチャ解析についてたまに質問を受けるため,簡単にここにまとめておきます.
テキスチャ解析概要
テクスチャ解析(Texture Analysis)とは画像の質感を測定し,その測定値から画像の分類をする手法です."質感"といっても光沢やざらつき,周期性などさまざまな質感があり,これらそれぞれを測定するための種々の定義式があります.今回はそのなかでも,不均一性についてまとめます.
画像の正規化
撮影環境や画像中の一部だけ解析したいなど様々な理由のため,解析対象となる画像のサイズは往々にしてバラバラです.画像サイズだけでなく,輝度値(画像の明るさ)の範囲もバラバラです.このままでは,このバラバラの影響で被写体が同じでも異なる解析値になってしまいます.そこで,このバラバラの影響を抑制するため,正規化(ノーマライゼーション)を行います.輝度値の範囲は,画像の輝度値の最大値と最小値を1-64の64段階(段階数は任意)に変換することで正規化されたり,0から1の値で無段階で正規化されたりします.ただし,計算の都合上,テクスチャ解析では有段階で正規化することの方がおおいと思います.一方,画像サイズの正規化は画像をマトリックス(行列)に変換して正規化します.今回はGLCM, GLSZM,NGTDMを扱います.
GLCM: Gray-Level Co-occurrence Matrix
GLCMは行に解析中心画素の輝度値,列にその周辺の画素の輝度値をとります.そしてその行列の要素の値は周囲に輝度値jを持つ画素の数になります.例えば,上図のように,中心画素の値が5で周辺に輝度値4の画素が2つあれば行列Aの5行4列目の要素の値は2になります.最後に行列Aを画像全体の輝度値の合計で割って,撮影環境による画素数の差異(画像サイズの差異)を抑制します.これで,GLCMによる正規化が完了したので画像の質感(不均一性)を測定できます.測定方法は次のセクションに書きます.
GLCMの簡単な例を見てみます.下図は右方向に輝度の傾斜をつけた画像とそのGLCMです,GLCMの対角成分に確率が分布してます.中心画素の周りに類似した輝度があると,対角に確率が集中します.
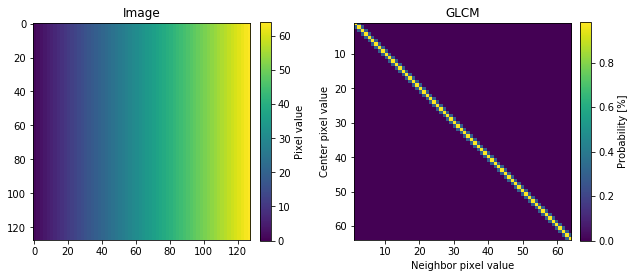
下図は右方向だけでなく下方向にも輝度の傾斜をつけた結果です.上図の例と同様に対角に確率が分布していることが分かります.しかし,対角の中央付近の確率が高く,周辺が低くなっています.これは,元画像中で輝度値が中央値である32付近を持つ画素が0付近や64付近よりも多いためにこのようになります.

最後にガウスノイズを付加した例を見ます.下図は上図の画像に平均0,標準偏差を輝度値レンジの20%のガウスノイズを付加しています(輝度値レンジ1-64のとき標準偏差は12.8).ノイズにより均一性が低下し対角から広がって確率が分布したことわかります.

GLSZM: Gray Level Size Zone Matrix
GLSZMは行に輝度値,列に連続している範囲の大きさをとります.そして,その要素の値は連続している大きさが何個あるかになります.例えば,上図のように,輝度値1で大きさ1の個数は1個,輝度値1で大きさ2の個数は2個になります.このようにして,作成されたマトリックスがGLSZMです.GLSZMを使った質感(不均一性)の測定は次のセクションに書きます.
GLSZMの簡単な例を見てみます.下図は右方向に輝度の傾斜をつけた画像とそのGLSZMです.GLSZMの列の値に少数点が出てますが,実際はsizeが256の列が1列です.元画像は輝度値1の画素が128行2列,輝度値2の画素が128行2列,輝度値3の画素が128行2列と輝度値64まで並んでいます.そのため,大きさ256(=128x2)のサイズが1-64の各輝度値で均等に観測されます.よって,このGLSZMは64行1列です.

下図は右方向だけでなく下方向にも輝度の傾斜をつけた結果です.斜め方向に同一輝度の画素が並ぶため,sizeにバリエーションが発生します.また,斜めに同一輝度を並べているため前記の右方向に輝度の差をつけた画像よりsizeの最大値が大きくなっていることわかります(右方向輝度傾斜の最大サイズ: 256 右下方向輝度傾斜の最大サイズ630).最大サイズが大きな値であるほど,画像内で均一である領域で多いことを示します.一方で,右方向だけに輝度の傾斜を与えたときはサイズのバリエーション(GLSAMの列数)が1だったことに対して,右下方向輝度傾斜の場合は620ものバリエーションがあります.サイズのバリエーションが増えることは,画像が様々なサイズを持つ均一な領域から構成されることであり,均一性は低下を示します.ゆえに,GLSZMは最大サイズが大きな値であってもGLSZMの列数の大小により(サイズのバリエーション数の大小)により均一性の高低を表す設計となっています.

最後にガウスノイズを付加した例を見ます.下図は右下方向輝度傾斜の画像に平均0,標準偏差を輝度値レンジの20%のガウスノイズを付加しています(輝度値レンジ1-64のとき標準偏差は12.8).ノイズにより均一性が低下しGLSZMの列数および最大サイズが低下していることがわかります(列数:9, 最大サイズ: 9).またGLSZMの値の最大値は輝度値32付近にあることが読み取れます.これは輝度値32付近の画素が多く画像に含まれていることを示しています.

NGTDM: Neighbourhood Gray-Tone-Difference Matrix
NGTDMは2段階の変換になります.1段目では中心画素を除いて,周辺画素の平均輝度を行列の要素値とする,平均値行列を作成します.すると,上図左の画像は上図中央のように変換されます.このとき,4つ角の画素等,周辺画素が8個ない画素は解析対象外とします(今回は周辺8画素を使って平均してますが,何画素で平均するかは任意です).そのため,画像の端に重要な画素のある解析は注意が必要です.2段階目では,平均値行列を作成したときに除外した中心画素の輝度値が共通な画素の平均値を合計します.2段階目の行列(NGTDM)は行に中心画素の輝度値をとり,列は1列だけです.そして,NGTDMの値は,「中心画素」と「周辺画素の平均」の差の絶対値の合計です.
上図のように,中心画素の値が2である平均値行列の値は「16/8」と「18/8」の2つです.そして,中心と周辺平均の差の絶対値は「|2-16/8|」と「|2-18/8|」です.最終的のこの2つの合計「0+0.25」がNGTDMの値になります.NGTDMを使った質感(不均一性)の測定は次のセクションに書きます.
NGTDMの簡単な例を見てみます.下図は右方向に輝度の傾斜をつけた画像とそのNGTDMです.周辺8画素を使って平均画像を計算しています.元画像は輝度値1の画素が128行2列,輝度値2の画素が128行2列,輝度値3の画素が128行2列と輝度値64まで並んでいます.前述したとおり周辺8画素が集まらない画素は計算から除外されます,そのため,中心画素の輝度値が1と64のそれぞれ1列分が計算に含まれません.そのため,NGTDMの1行目と64行目の値がその他の行に対して低くなっています.

下図は上図の元画像中心を輝度値64に置き換えた結果です.この結果からわかるように,NGTDMは周辺の平均と差が大きい輝度値を持つ画素の検出力が高いです.NGTDMの64行目が最大となるのは,輝度値64(画像中心の縦線)の画素は左右に輝度値の差があるためです.それに対してNGTDMの31行目は左右の片側だけに大きな輝度差が生じていることを検出しているため,64行目の半分程度の値となります.

下図は右方向だけでなく下方向にも輝度の傾斜をつけた結果です.NGTDMの32行目あたり最大となっていることがわかります.これは,NGTDMは中心画素の輝度値が32である画素が他の輝度値を持つ画素の数より多いためです.よって,NGTDMは周辺画素と中心画素の輝度差および中心画素の画素値の発生頻度の2つに感度を持ちます.よってNGTDM,周辺画素との輝度差が大きく且つその中心画素輝度値が頻繁に発生するものには大きな重みを与え,周辺画素との輝度差が大きくても,その中心画素の輝度値の発生頻度が低ければ小さな重みを与えます(前者に対して後者は相対的に重視しない).

質感(不均一性)の測定
GLCMの場合
GLCMへ正規化したのち不均一性を測定する尺度に以下があります.
"uniformity", "entropy", "dissimilarity", "contrast", "homogeneity", "inverse difference moment", "maximum probability"
すべての定義を書くのは大変なので,"entropy"と"dissimilarity","homogeneity"を解説します.(コメントをいただければ,その他の解説も後日加筆します.)
Entropy
$$
-\sum_{i,j} P(i,j) \log P(i, j) \tag{1}
$$
GLCMの要素値は中心画素値iで周辺に画素値jの画素がある確率と解釈することができます.
そのためここでは,GLCMをP(probabilityの頭文字)と表記してます.エントロピーは情報量と日本語に訳される通り,この事象を表現するのに必要な量を示しています.たとえば,サイコロの目のどれが出たかを伝達するときに必要な情報量(0と1の2進数の情報量)は
$$
- \sum_{i=1}^6 (\frac{1}{6} \log_2 \frac{1}{6} ) \fallingdotseq 2.58
$$
これはこのサイコロの出目の伝達に約2.58ビット(2進数で2.58桁の意)必要だということを示しています.ご存知の通り離散的なコンピュータの世界で2.58ビットは表現できないので切り上げて3ビット(2進数で3桁,10進数の0-7を表現できる)となります.ここで,このサイコロが細工により1-3の3パターンしか出ないとすると,出目の情報を伝達するために必要な情報量は
$$
- \sum_{i=1}^3 (\frac{1}{3} \log_2 \frac{1}{3}) - \sum_{i=4}^6 (0 \cdot \log_2 0 ) \fallingdotseq 1.58
$$
1.58ビットの情報量があればいいとなります(実用上は切り上げて2ビット),以上のように,最もランダムな状態(不均一)のとき必要な情報量(エントロピー)は大きくなり,規則性がある状態(均一性をもつ)とき情報量は小さくなります.この情報量による指標を用いてGLCMから不規則性を測定する方法が式1です.
Dissimilarity
$$
\sum_{i,j} P(i,j) |i-j| \tag{2}
$$
|i-j|は中心画素値と周辺画素値の差の絶対値です.均一な画像であれば|i-j|=0あたり(GLCMの対角成分)に確率が分布し,不均一な画像であれば|i-j|>0に確率が分布すると考えられます.そこで,|i-j|の期待値(平均値)を使って不均一性を測定する方法が式(2)になります.Dissimilarityという名前の通り,不均一性が高いと大きな値となり,不均一性が低い(きんいつである)ほど0に近づきます.
Homogeneity
$$
\sum_{i,j} \frac{P(i,j)}{1+|i-j|} \tag{3}
$$
HomogeneityはDissimilarityの|i-j|を分母に持ってきて,均一な画像であるほど値が高くなるように尺度を反転させた指標です.分母が0になって割り算ができなくなるのを回避するため分母に1が足されています.なので,実質,HomogeneityとDissimilarityは同じものです.均一であることを説明するときには,homogeneityを使って「均一な画像であるほど値が高い」と説明する方が,dissimilarityを使って「均一な画像であるほど値が低い」と説明するより分かりやすいですね.不均一性の指標にはDissimilarity,均一性の指標にはHomogeneityを使うといいでしょう.
GLSZMの場合
GLSZMへ正規化した後に不均一性をを測定する尺度に以下があります.
"small_area_emphasis", "large_area_emphasis" ,"low_intensity_emphasis", ,"high_intensity_emphasis", "intensity_variability", "size_zone_variability", "zone_percentage",
"low_intensity_small_area_emphasis", "high_intensity_small_area_emphasis", "low_intensity_large_area_emphasis", "high_intensity_large_area_emphasis"
すべての定義を書くのは大変なので,"intensity_variability"と"size_zone_variability","zone_percentage"を解説します.(コメントをいただければ,その他の解説も後日加筆します.)
Intensity variability (IV)
$$
\frac{1}{\Omega} \sum_{i=1}^M \left[ \sum_{j=1}^N \frac{z(i, j)} {i^2}\right]^2 \tag{4}
$$
ΩはGLSZMの総和値,z(i,j)はGLSZMのi行j列目の値,MはGLSZMの行数,NはGLSZMの列数です.
下図に示すように,IVでは,はじめに列方向にGLSZMを総和して,サイズ情報(同じ輝度値を持つ画素の連続している大きさ)を消します.これにより,M行1列の行列になります.次に,重みとして輝度値の-2乗(行方向の値の-2乗)を掛けます.これにより,低輝度側に大きな重み,高輝度側に低い重みを与えます.最終的に重みを掛けたM行1列の行列を総和し,異なる画像間でのゾーン総数の違いをキャンセルするためにΩで割ります.よって,IVは低輝度に画素が集中しているときに相対的に大きな値となり,高輝度側に画素が集中すると小さな値となります.ゆえに,この指標では低輝度側に均一性があるのか,それとも高輝度側に均一性があるのかを示しているといえます.
Size-zone variability (SV)
$$
\frac{1}{\Omega} \sum_{j=1}^N \left[ \sum_{i=1}^M \frac{z(i, j)} {j^2}\right]^2 \tag{5}
$$
IVがサイズ情報を消したことに対して,SVは輝度(行方向)情報をGLSZMから消去します.まず,下図に示すように,GLSZMを行方向に総和し1行N列の行列を作成します.そしてこの行列に,サイズ(列方向の値)の-2乗を掛けます.これにより,サイズが小さい側に大きな重み,サイズが大きい側に小さな重みが与えられます.最終的に重みを掛けた1行N列の行列を総和し,IV同様に異なる画像間でのゾーン総数の違いをキャンセルするためにΩで割ります.よって,SVは画像が小さいサイズのゾーンで構成される時に大きな値となり,大きなゾーンで画像が構成される時に小さな値となります.ゆえに,この指標は,画像が均一である(同じ輝度が連続している)とき小さな値となり,画像が不均一(輝度の連続性が低い)とき大きな値となります.
Zone percentage (ZP)
$$
\frac{\Omega}{\sum_{i=1}^M \sum_{j=1}^N j^2 z(i, j)} \tag{6}
$$
ZPはSV同様に輝度方向の情報をGLSZMから削除します.まず,下図に示すように,GLSZMを行方向に総和し1行N列の行列を作成します.そしてこの行列に,サイズ(列方向の値)の+2乗を掛けます.
これにより,サイズが小さい側に小さな重み,サイズが大きい側に大きな重みが与えられます.最後に,その名が示すとおり,ゾーン数に対する割合ですから,Ωを重み付けした1行N列の行列で割ります.よって,ZPはサイズが大きいゾーンが画像上で支配的なとき小さな値,反対に,サイズが小さいゾーンが画像上で支配的なとき小さな値となります.ゆえに,ZPはSVとほぼ同様な指標です.ただし,ZPの値の範囲は0-1となるため,SVより均一性の度合いを値をみただけでつかめるメリットがあります.
NGTDMの場合
NGTDMへ正規化したのち不均一性を測定する尺度に以下があります.
"coarseness", "contrast", "busyness", "complexity", "strength"
コメントを頂いた,"coarseness"と"busyness"を解説します.
Coarseness
$$
\frac{1}{\epsilon + \sum_{i=1}^N p_i s(i)}\tag{7}
$$
$$
p_i = \frac{N_i}{M}
$$
ε分母が0にならないようにするための1e-6等の小さな数,Nは画像の輝度値の最大値と最小値で正規化したときの段階数,s(i)は中心画素の輝度がiのNGTDMの値,Niは輝度値iを持つ画素の数,Mは平均値行列の要素数です.piの分母に平均値行列の要素数を使用するのはNGTDMは画像の端を解析から除外するため,除外後の解析に使用した画素数として平均値行列の要素数を使用します.よって,piは画素値iを持つ画素の発生頻度(出現確率)です.したがって,εを除く分母はNGTDMの期待値となります.ここで,NGTDMの期待値は解析に使用した画像全体での中心画素と周辺画素との差の合計の期待値となります.中心画素と周辺画素との差が大きいとき(画像が不均一のとき)分母は大きい値となり,結果としてCoarsenessは小さくなります.反対に,周辺画素との差が小さいとき(画像が均一のとき),分母は小さい値となり,結果としてCoarsenessは大きくなります.
Busyness
$$
\frac{\sum_{i=1}^N p_i s(i)}{\sum_{i=1}^N\sum_{j=1}^N |ip_i -jp_j|} \tag{8}
$$
$$
ip_i \neq 0, jp_j \neq 0
$$
分子はNGTDMの期待値で,中心画素と周辺画素の差の合計の期待値となります.つぎに,分子はjに関してだけ総和を計算すると
$$
\sum_{i=1}^N |Nip_i -E(J)|
$$
となります.ここで,E(J)は画像の輝度値の期待値です.画素値がE(J)で表される期待値付近に集中しているとき(ヒストグラム的に不均一なとき),i=E(J)付近では,N i Pi と E(J)は,類似した値であるため|N i Pi - E(J)|は小さくなります.一方でiがE(J)から離れているところでは,Pi(iの出現確率)が小さいため|N i Pi - E(J)|も小さくなります.よって,画素値の均一性が低いとき(一部の画素値に集中しているとき)は分母が小さくなり,busynessは大きな値となる傾向です.一方で,画素値の出現頻度が一様なとき(どの輝度値も同程度の数で画像中に分布するとき)は,iがE(J)から離れているところにおいても,Pi(iの出現確率)がi=E(J)付近のときと比較して相対的に小さくならないため,|N i Pi - E(J)|が小さくならず,分母が大きくなりbusynessは低下する傾向になります.
ここで,重要なのは,分子は周辺画素との差から生じる不均一性の検出し(空間的な不均一性),分母は輝度値の出現頻度による不均一性(ヒストグラム的な不均一性)を検出していることです.そのため,空間的に均一であっても,ヒストグラム的に不均一であればbusynessは比較的大きな値となります.具体的には,下図において,左側の画像のほうが均一に思えますがbusynessの値は202.4と不均一性の高い結果となります.busynessの分母はヒストグラムの均一性であることに注意してください.

実装
テクスチャ解析のPET画像用のPython実装をGitHubで公開してます.
あとがき
私が誤った理解をしている点や内容が不正確な点がありましたらコメントにてご指摘いただけますと幸いです.





