私事ですが、カミさんが慶應の通信で学んでいて今年の夏期スクーリングで統計学をとっています。と言ってもカミさんは数学も統計もド素人ですし、それは私も分かっているので分からんことは直ちに私に尋ねろと言っています。で、今回は統計学の初っ端、度数分布に絡む色々なことを訊かれたので、それに関するまとめを載せてみました。1
なお、我が国では学習指導要領や学校の進度により、統計学に関する初等的な事柄をほとんど学ばずに(あるいは学べずに)高校・大学を卒業した人も多いと思います。昨今の学習指導要領ではプログラミング教育だ統計資料の活用だアクティブラーニングだと統計学まわりのことは重視されているので、若年層はある程度大丈夫かもしれませんが。
統計初心者が学部レベルの統計学を履修する際に、最初に読むとよいとネット等で言われる教科書に以下のものがあります。
鳥居泰彦 (1994) 『はじめての統計学』日本経済新聞社, ISBN-13: 978-4532130749.
とは言え、数学やら統計から離れて10年以上経つような「真正のド素人」には、この本でもつまづく箇所が多いという意見がツイッターなどでは見られます。『はじめての統計学』でもカバーしきれない「かゆい所」に手が届くような記事になればと思い、色々と書いていこうかと思います。2
度数とヒストグラム
そもそも私は「度数」という言い方は嫌いです。なぜなら、おそらく日常的にこの用語を使う人はほとんどおらず、常用語とは言い難いと思うからです。度数と同じ意味として教科書等で紹介される「頻度」の方がまだ一般的な言葉だと思います。また度数の英訳は frequency ですが、この言葉の和訳として思い浮かぶのは「頻度」ではないでしょうか。とは言え「頻度分布表」とはあまり言わないので、ガマンしてここでは度数分布表という言葉を使いますが…
今回はRも適宜使って度数分布表やヒストグラムまわりの説明をしたいと思います。例として、以下の28人ぶんの身長データを考えましょう。
data <- c(144.5, 165.8, 156.7, 146.2, 170.7,
172.4, 158.8, 153.1, 163.0, 166.2,
173.1, 142.9, 149.8, 157.6, 162.1,
168.9, 147.7, 157.8, 168.9, 170.2,
156.7, 163.8, 168.9, 169.7, 157.8,
159.7, 157.6, 179.5)
簡単に説明すると、一人目の身長144.5cm、二人目の身長165.8cm、...、28人目の身長179.5cmというデータ列を data という変数名に代入したものです。
度数分布表と言いましたが、まずはヒストグラムを出力してみましょう。Rでは以下のように hist 関数を使えば簡単に出力できます。
result <- hist(data, breaks=c(140,150,160,170,180),
main="ヒストグラム",
xlab="身長",
ylab="度数(頻度)",
ylim=c(0,10), col="aquamarine2")
ちなみに、breaks は階級幅です。あとの main = などなどはそれぞれグラフ名、縦軸名、横軸名、縦軸の最小・最大値、グラフの色の設定です。
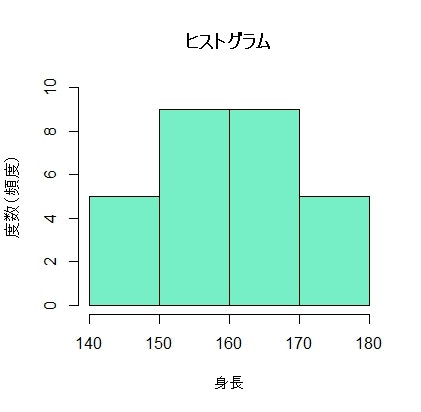
で、以下のようなグラフ(ヒストグラム)が出力されます。
まあ、このヒストグラムとやらが何を表しているのかは直感的に分かると思います。140-150cmの身長の人が5人、150-160cmの身長の人が9人、160-170cmの身長の人が9人、170-180cmの身長の人が5人ということを表しています。こうした「140-150cm」のようなクラスを階級といいます。
度数分布表
「140-150cmの身長の人が5人、150-160cmの身長の人が9人、160-170cmの身長の人が9人、170-180cmの身長の人が5人」というのを表にしたのが度数分布表です。以下のようになります。(厳密には度数分布表をつくってからヒストグラムをつくるのがマナーのようですが、プログラムで処理する現代ではその順番に固執する必要性はもはやないでしょう…)
| 階級 (cm) | 度数 (人) |
|---|---|
| 140以上150未満 | 5 |
| 150以上160未満 | 9 |
| 160以上170未満 | 9 |
| 170以上180未満 | 5 |
と、ここまでは小学校低学年でもいけるレベルだと思います。
次に相対度数を考えます。
ここまでのポイント
- 〇〇以上〇〇未満という幅にどれだけのデータがあるか、というのを表したものが度数分布表である
- 〇〇以上〇〇未満という幅を階級という
- それぞれの階級内にあるデータ数を度数という
- 横軸に階級、縦軸に度数をとった棒グラフをヒストグラムという
相対度数
上記で考えた度数はいわば絶対度数です。つまり、他の階級の度数なんて関係なく、140-150cmの人、150-160cmの人、...をカウントした数値です。「俺のクラスの出席者は30人いる、他クラスの出席者なんて知らん」という感じです。しかし統計学は考えている対象全体の中での量や位置を気にします。つまり相対的な量や位置にフォーカスします。「他のクラスの出席者全体の中での、俺のクラスの出席者は〇〇パーセントだ」というのを気にするということです。
そこで140-150cmの人、150-160cmの人、...は、それぞれ全体の中でどれくらいの割合いるのかな、というのを求めます。これを相対度数といいます。
今回は全体で28人いるので、それぞれの度数を28で割ればいいだけですね。次のようになります。なお、メンドイので小数化しません。
| 階級 (cm) | 度数 (人) | 相対度数 |
|---|---|---|
| 140以上150未満 | 5 | $\frac{5}{28}$ |
| 150以上160未満 | 9 | $\frac{9}{28}$ |
| 160以上170未満 | 9 | $\frac{9}{28}$ |
| 170以上180未満 | 5 | $\frac{5}{28}$ |
この28人からランダムに1人を選ぶ場合、相対度数はその選んだ人がそれぞれの階級に属する確率を表します。これも直感的に分かると思います。
累積相対度数
確率は全ての事象を考慮したら1(つまり100パーセント)です。ですから、上記の表のすべての階級の相対度数を足したら1です。これは実際に計算してみても分かると思います。
また、140-150cmの相対度数と150-160cmの相対度数とを足すと$\frac{5+9}{28} = \frac{14}{28}$(あえて約分しません)ですが、これは「ランダムに選んだ1人が160cm未満である確率」を表します。これも直感的に分かると思います。
このように各階級の相対度数を次々に足していった値を累積相対度数といいます。以下のようになります。(やはりあえて約分しません。しかし、試験では約分しましょう)
| 階級 (cm) | 度数 (人) | 相対度数 | 累積相対度数 |
|---|---|---|---|
| 140以上150未満 | 5 | $\frac{5}{28}$ | $\frac{5}{28}$ |
| 150以上160未満 | 9 | $\frac{9}{28}$ | $\frac{5+9}{28} = \frac{14}{28}$ |
| 160以上170未満 | 9 | $\frac{9}{28}$ | $\frac{5+9+9}{28} = \frac{23}{28}$ |
| 170以上180未満 | 5 | $\frac{5}{28}$ | $\frac{5+9+9+5}{28} = \frac{28}{28} = 1$ |
ここまでのポイント
- 全ての階級の度数の和、すなわち全データ数(サンプル数)で各階級の度数を割ったものを相対度数という
- 相対度数は、対象とするデータ全体の中で各階級に属するデータ数の割合を表すものである
- また、相対度数は、ランダムに一つのデータを選んだとき、そのデータがその階級に属する確率を表したものである
- 対象とする階級までの相対度数の和を累積相対度数という
- 例えば、対象とする階級が$a$以上$b$未満であるとき、その階級までの累積相対度数は、ランダムに選んだ一つのデータが$b$未満の階級に属する確率を表したものである
- いちばん大きい階級までの累積相対度数、上記例で言えば170以上180未満の階級までの累積相対度数は、$\frac{全データ数}{全データ数}$に他ならないので、1となる
- これは全事象の確率が1であることと同様である
ヒストグラム・度数分布表における平均
平均と一言で言っても色々な平均があります。実際に統計調査を行ったとして、今回のように data <- c(144.5, 165.8,...,179.5) と具体的なデータ列が得られる調査を行えた場合、厳密な算術平均、すなわち小学校で習うような全ての数値の和をデータの個数で割った平均が求められます。以下のように、Rでは mean 関数を使えば簡単に出ます。
mean(data)
この値は 161.075 となります。
一方、もし上記の度数分布表のようなデータしか得られない場合、すなわち具体的なデータ列ではなく階級とそれぞれの階級に属する度数しか得られない場合はどうでしょうか?
実際に、年収などのプライバシーに関わるような調査では、「年収○○万円以上○○円未満が○○人」のように、具体的に「342万円の人、296万円の人、...」のようなデータではなく階級とそれに属する人数しか得られないことがよくあります。この場合、当然ですが上記の161.075のように厳密な平均値を求めることはできません。
こういうときは、それぞれの階級に属する人たちは、全員の身長がある代表値だと仮定して(仮想的な)平均値を求めることが一般的です。代表値として、階級幅の中央値(または平均値)が使われることが多いです。つまり、「140cm以上150cm未満の5人は全員145cm、150cm以上160cm未満の9人は全員155cm、...だと仮定する」ということです。
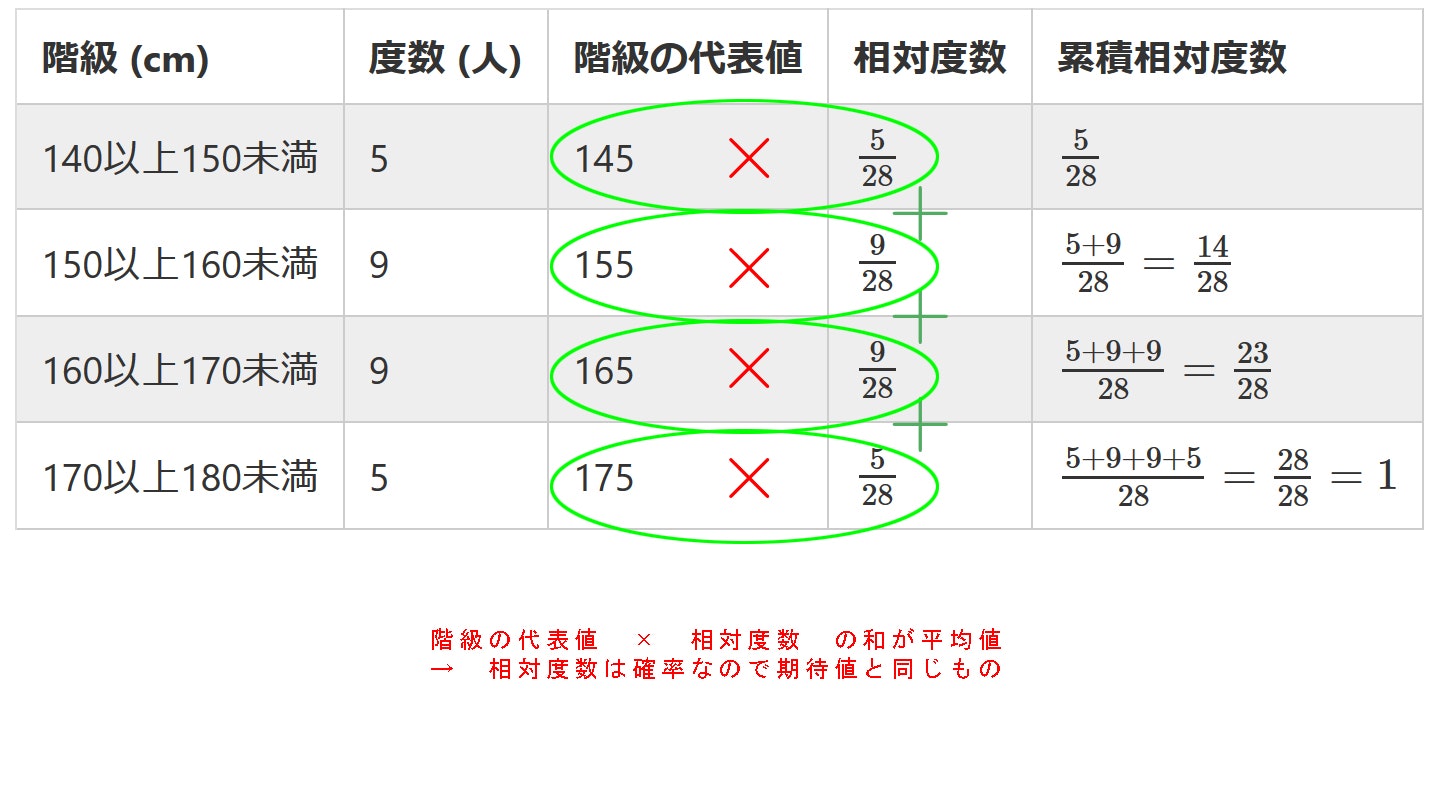
各階級の代表値として中央値をとった列を加えた度数分布表は以下の通りです。
| 階級 (cm) | 度数 (人) | 階級の代表値 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 140以上150未満 | 5 | 145 | $\frac{5}{28}$ | $\frac{5}{28}$ |
| 150以上160未満 | 9 | 155 | $\frac{9}{28}$ | $\frac{5+9}{28} = \frac{14}{28}$ |
| 160以上170未満 | 9 | 165 | $\frac{9}{28}$ | $\frac{5+9+9}{28} = \frac{23}{28}$ |
| 170以上180未満 | 5 | 175 | $\frac{5}{28}$ | $\frac{5+9+9+5}{28} = \frac{28}{28} = 1$ |
このように考えると、この仮想的な平均値は以下のように表せます。$N$は全サンプル数(つまり度数の和)です。
\mathrm{(度数分布表での平均値)} = \frac{1}{N}\sum_{i=1}^{階級の個数} (i番目の階級の代表値) \times (i番目の階級の度数)
なお、$\frac{1}{N}\times (i番目の階級の度数)$というのは相対度数のことですから、以下のようにも表せます。
\begin{eqnarray*}
\mathrm{(度数分布表での平均値)} &=& \frac{1}{N}\sum_{i=1}^{階級の個数} (i番目の階級の代表値) \times (i番目の階級の度数)\\
&=& \sum_{i=1}^{階級の個数} (i番目の階級の代表値) \times (i番目の階級の相対度数)
\end{eqnarray*}
相対度数というのは上述したように「ランダムに選んだ1人がその階級に属する確率」ですから、実は$\sum_{i=1}^{階級の個数} (i番目の階級の代表値) \times (i番目の階級の相対度数)$というのは$(i番目の階級の代表値)$をスコアとする確率の期待値に他なりません。期待値のことを確率的な平均値と呼ぶ理由はこうしたことからも分かるでしょう。
今回の身長の例では、度数分布表における平均値はRで次のように計算できます。
(as.vector(result$counts) %*% as.vector(result$mids))/sum(as.vector(result$counts))
result という変数にヒストグラムの結果を代入しましたが、このとき result$counts には各階級の度数が、result$midsには各階級の中央値が格納されていますので、result$counts と result$mids とをベクトル型に変換してその内積をとれば$\sum_{i=1}^{階級の個数} (i番目の階級の代表値) \times (i番目の階級の度数)$が計算できます。あとは全サンプル数、すなわち result$counts の和で割ればいいだけです。
この結果は 160 となります。
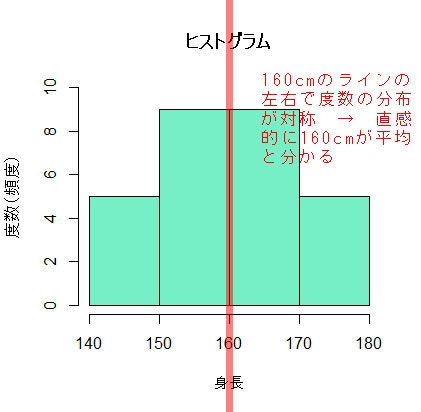
もちろん、今回はわざと左右対称なヒストグラムになるようデータ列を作ったので、以下の図のように直感的に160がヒストグラムの平均値だと分かると思います。そして、この直感と一致する結果となりました。
さて、一目瞭然ですが元のデータ列から計算した算術平均値は161.075でしたが、度数分布表から得られる概算的な平均値は160で、違いがありました。統計的手法を使う目的は真実の値になるべく近い値を得ることですので、多少のずれがあることは許容します。ですから、各階級に属するデータは全員その階級の代表値だという仮定(まさに仮定)を置くわけです。
ここまでのポイント
- 度数分布表における平均値とは、$\frac{1}{全データ数}\sum_{階級i}階級iの代表値 \times 階級iの度数$である
- 階級の代表値は別途計算する必要があるが、簡単な例では階級幅の平均値が利用される
- $\frac{1}{全データ数}\times 階級iの相対度数=階級iの相対度数$なので、上記の式は$\sum_{階級i}階級iの代表値 \times 階級iの相対度数$としてもよい
- 相対度数を使った上記の式は、確率変数の期待値と同様のものである
- データの各要素の値から求めた算術平均と、上記のように求める度数分布表の平均値は必ずしも一致するとは限らない
確率変数
世の中のほとんどの値は確率変数とみなせます。すなわち、ランダムに変化する値とみなせます。なぜなら、例えば身長や体重でさえ、睡眠時間の変動・摂取カロリー量の変動・その日の運動量や発汗量などの変動・計測地点の重力加速度のブレ・計測機器の誤差などなどから、厳密な値(それこそナノスケール以下の極小の値まで考えた厳密な値)を確定的に求めることはおよそ不可能と言えるからです。確率変数は実際に値が計測・観測されるまで分からないヴェールに包まれた物とみなせるでしょう。逆に、計測・観測されると実際の値として目に見えるものとなります。このように実際に観測された確率変数の特定の値を実現値といいます。よって、身長や体重、死亡時年齢、今日の歩数、などなど、これらの数値は正確に言うと確率変数の実現値と言えます。
今回の例で扱った身長データの度数分布表やそれを視覚化したヒストグラムは、身長という確率変数の実現値の分布を表したものと捉えることができます。確率変数の分布を把握することは統計分析の上で重要です。確率変数が離散的である場合と連続的である場合に分けてみていきましょう。
確率関数
身長は厳密に言えば連続的な確率変数と言えるでしょう。これに対して、コインの裏表、サイコロの目、ルーレットの目、麻雀の点数、ガチャで得られるものなど、ギャンブルで使われる多くの目・点数などは離散的な確率変数でしょう。
サイコロの目を確率変数$X$とすると$X$は6通りの値をとりますし、ルーレット(カジノのルーレットはちょっと目が多いので人生ゲームのルーレットとすると)の目を確率変数$X$とすれば10通りの値をとります。
サイコロの目$X$でいうと、$X=3$となる確率$P(X=3)$、すなわち「3の目が出る確率」は$P(X=3)=\frac{1}{6}$です。$X$が離散的な確率変数の場合、このように$X$がちょうど特定の値をとるときの確率が求められます。
上記サイコロの例のように、確率変数$X$がある値$x$をとるときの確率は$P(X=x)$と表すことができますが、これが表す値、すなわち具体的な確率の値を$f(x)$とおきます。つまり、$f(x)=P(X=x)$です。この$f(x)$を確率関数とか確率質量関数と言います。
確率関数$f(x)$の値は度数分布表でいうところの相対度数です。ですから、相対度数を縦軸にとったヒストグラムはまさに確率関数の概形と言えます。
離散型確率分布
確率関数の和を計算することは累積相対度数を求めることと同じと言えます。確率関数の和を離散型の累積分布関数(または単に分布関数)といい、記号で$F(x)$と書きます。
F(x) = \sum_{x_i \le x} f(x_i)
上式の$\sum$の中では、離散的な値を考えればよいので明示的に$x_i$という$i$番目を強調した書き方をしています。$f(x)$は確率そのものですから0以上です。そういう0以上のものを足していくわけですから、累積分布関数は増加(非減少)していく関数です。さらに言えば確率変数は離散的な値をとるわけですからグラフは階段状に上がっていく形をしています。
離散型の累積分布関数を表す私が好きな喩えは「入金専用の銀行口座の残高」です。入金専用なのでお金が入ってくることはあっても出ることはない口座です。(いつその金を使うんだって突っ込みはナシで…)
このような口座の残高をチェックすると、ATMに表示される残高は要するにチェック時期までの累積入金額であることは容易に想像できるでしょう。$\sum_{x_i \le x} f(x_i)$における$x$は残高チェックの時間で、要するにそれまでの入金額$f(x)$の和が残高、すなわち累積分布関数の値ということです。(もちろん、実際は$f(x)$は確率ですから0以上1以下の数字ですので、1通貨単位以上のものを扱うお金とは違いますけど…)
ということで、多くの場合、離散型の累積分布関数は以下のような場合分けの形で定義されます。
F(x) = \begin{cases}
p_0 \hspace{1em} (x < a_0) \hspace{1em}(階段の0段目) \\
p_1 \hspace{1em} (b_1 \le x < a_1)\hspace{1em}(階段の1段目) \\
p_2 \hspace{1em} (b_2 \le x < a_2) \hspace{1em}(階段の2段目) \\
\cdots \\
p_k \hspace{1em} (b_k \le x) \hspace{1em}(最上段)
\end{cases}
確率関数の和、すなわち累積分布関数が分かれば、$X$が〇〇以上〇〇以下の値をとる確率というような幅をもったときの確率を求めることもできます。例えばサイコロ目$X$が1以上4以下になる確率は、$P(1\le X \le 4) = f(1) + f(2) + f(3) + f(4) = F(4) = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{2}{3}$です。
また、累積分布関数を用いてサイコロの目$X$が特定の値、例えば4をとるときの確率を求めることもできます。それは次のように計算できます。
\begin{eqnarray*}
&&P(X=4) \\
&=& P(1\le X \le 4) - P(1 \le X < 4) \\
&=& P(1 \le X \le 4) - P(1 \le X \le 3) \\
&=& F(4) - F(3) \\
&=& \frac{4}{6} - \frac{3}{6} \\
&=& \frac{1}{6}
\end{eqnarray*}
ここまでのポイント
- 相対度数の和が累積相対度数であったのと同様、確率関数$f(x)$の和を累積分布関数$F(x)$という
- 正確には、累積分布関数$F(x)$は、$x_i \le x$の確率関数$f(x)$の和である
- すなわち$F(x) = \sum_{x_i \le x}f(x_i)$である
- 確率$P(X)$の表記を使うと、$F(x) = P(X \le x)$である
- つまり確率変数が$x$以下となる確率(言い換えれば$x$以下になる確率の総和)が$F(x)$である
確率密度関数
一方、連続的な値をとる確率変数$X$を考えると、確率はどのように求めることができるのでしょうか?
直感的に分かると思いますが、確率関数は連続的になり、〇〇以上〇〇以下のような幅をもったときの確率は確率関数の和ではなく積分計算をすることが分かるでしょう。
では、連続的な確率変数$X$がちょうどある値をとるときの確率はどのように計算できるのでしょうか?
これはゼロとなります。ゼロとなる理由については、以下のような説明ができるかもしれません。
離散量の場合は、例えばサイコロの目でちょうど4が出る確率を「4以下の目が出る確率から4未満の目が出る確率を引いたもの」と考えて、既に述べたように$P(1\le X \le 4) - P(1 \le X < 4)$のように計算できます。つまり確率変数の「1以上4以下の和から1以上4未満の和を引く」計算をします。ただし、離散なので$P(1 \le X < 4) = P(1 \le X \le 3)$となりますから、実際に計算するのは$P(1\le X \le 4) - P(1 \le X \le 3)$です。
一方、連続量の例として体重を考えるとき、体重がちょうど50kgになる確率は同様に$P(0\le X \le 50) - P(0 \le X < 50)$を計算すれば求められます。つまり離散確率変数でいうところの確率関数のようなものを「0以上50以下で積分したものから0以上50未満で積分したものを引く」という計算をすることになります。しかしこうした積分範囲では50以下と50未満を区別しません。というのも、ちょうど50という点を積分しても面積は0(なぜなら線は太さを持たないので面積はゼロ)だからです。ですから体重という連続確率変数では$P(0\le X \le 50)$と$P(0 \le X < 50)$は等しいので、$P(0\le X \le 50)-(0 \le X < 50)=0$です。
つまり、連続確率変数でちょうどある値の確率を求めることは「線分の面積を求めろ」と言っているに等しく、答えとしては「そんなものはゼロに決まっている」となります。従って、連続確率変数ではちょうどある値の確率を求める作業に大した意味はなく、重要なのは確率変数がある範囲をとる確率を求めることとなります。
連続的な確率変数$X$がある値$x$以下をとる確率$P(X \le x)$が関数$f(t)$を$-\infty$から$x$まで積分した値で表せるとき、$f(t)$を確率密度関数と言います。つまり以下が成り立ちます。
P(X \le x) = \int_{-\infty}^{x} f(t)dt
このような確率密度関数の積分も、度数分布表でいうところの累積相対度数に相当します。
また、この確率密度関数の積分$\int_{-\infty}^{x} f(t)dt$が連続型の累積分布関数$F(x)$になります。つまり$F(x) = \int_{-\infty}^{x} f(t)dt$です。
なお、身長は厳密に考えれば連続量と書きましたが、今回の身長の例でも相対度数を縦軸にとったヒストグラムの幅を限りなくゼロに近づければ、確率密度関数の概形と同じものが得られます。
応用で、連続的な確率変数$X$がある値$y$以上$x$以下をとる確率は、$P(y \le X \le x) = \int_{y}^{x} f(t)dt$となります。
質量や密度という言い方について
上記の例では連続確率変数がちょうどある値をとるときの確率がゼロとなることを、線分と面積というもので説明しましたが、「切り口と質量の関係」は「線分と面積」と似た関係にあるでしょう。
頭の中でイメージすれば分かると思いますが、線分が移動したときに描く図形(軌跡)は面積を持ちます。しかし、線分それ自体の面積はゼロです。
同様にある立体の切り口をみて、「この切り口の質量ってどれだけ?」と訊いても「切り口に質量なんてない」と答えるでしょう。しかし切り口が動くときの軌跡は立体になるので、その立体は確かに質量を持ちます。
つまり、連続確率変数がある特定の値をとるときの確率を尋ねることは、切り口の質量を尋ねるようなものです。質量は平面に厚みが、つまり体積があってはじめて生まれるものですから、切り口だけでは質量ゼロです。
密度という言葉を使っても同様で、密度(単位体積当たりの質量)が定義されているものに体積を与えてはじめて質量が生まれます。
離散的な確率変数を考える場合は、特定の値$x$に対する確率、すなわち質量をとることができます。しかし、連続的な確率変数を考える場合は、特定の値$x$に対して質量をとることはできません。ですから、質量をとるためには質量の源である密度の積分を考える必要があるわけです。
確率質量関数、確率密度関数における質量、密度という言い方はこうした考えが背景にあると思われます。3また、測度論においては面積も確率も測度として抽象化されますが、こういったことも質量や密度と呼ぶ背景にあると思われます。4
いくつかの例
例題として、離散的な累積分布関数$F(x)$が与えられているとき、そこから確率質量関数$f(x)$を求め、さらにいくつかの確率を具体的に計算するような問題を考えてみましょう。
例題:
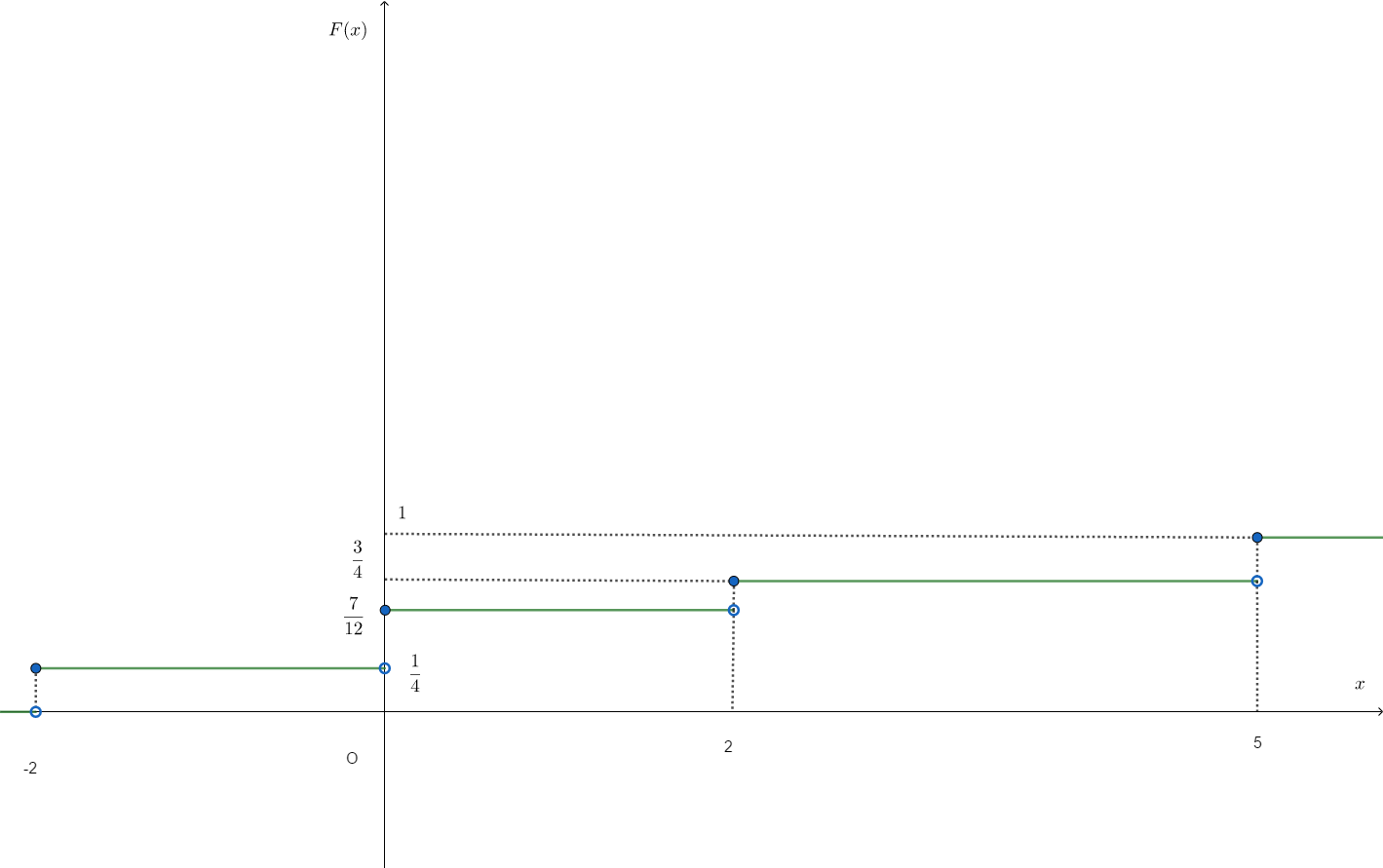
ある離散型の確率変数$X$について、次のような累積分布関数$F(x)$があるとき、これに対応する確率質量関数$f(x)$を求めよ。また、確率$P(X \le -2)$、確率$P(X < 2)$、確率$P(-1 \le X \le 1)$、確率$P(3<X<4)$をそれぞれ求めよ。
F(x) = \begin{cases}
0 \hspace{1em} (x < -2) \\
\frac{1}{4} \hspace{1em} (-2 \le x < 0) \\
\frac{7}{12} \hspace{1em} (0 \le x < 2) \\
\frac{3}{4} \hspace{1em} (2 \le x < 5) \\
1 \hspace{1em} (5 \le x)
\end{cases}
考え方:
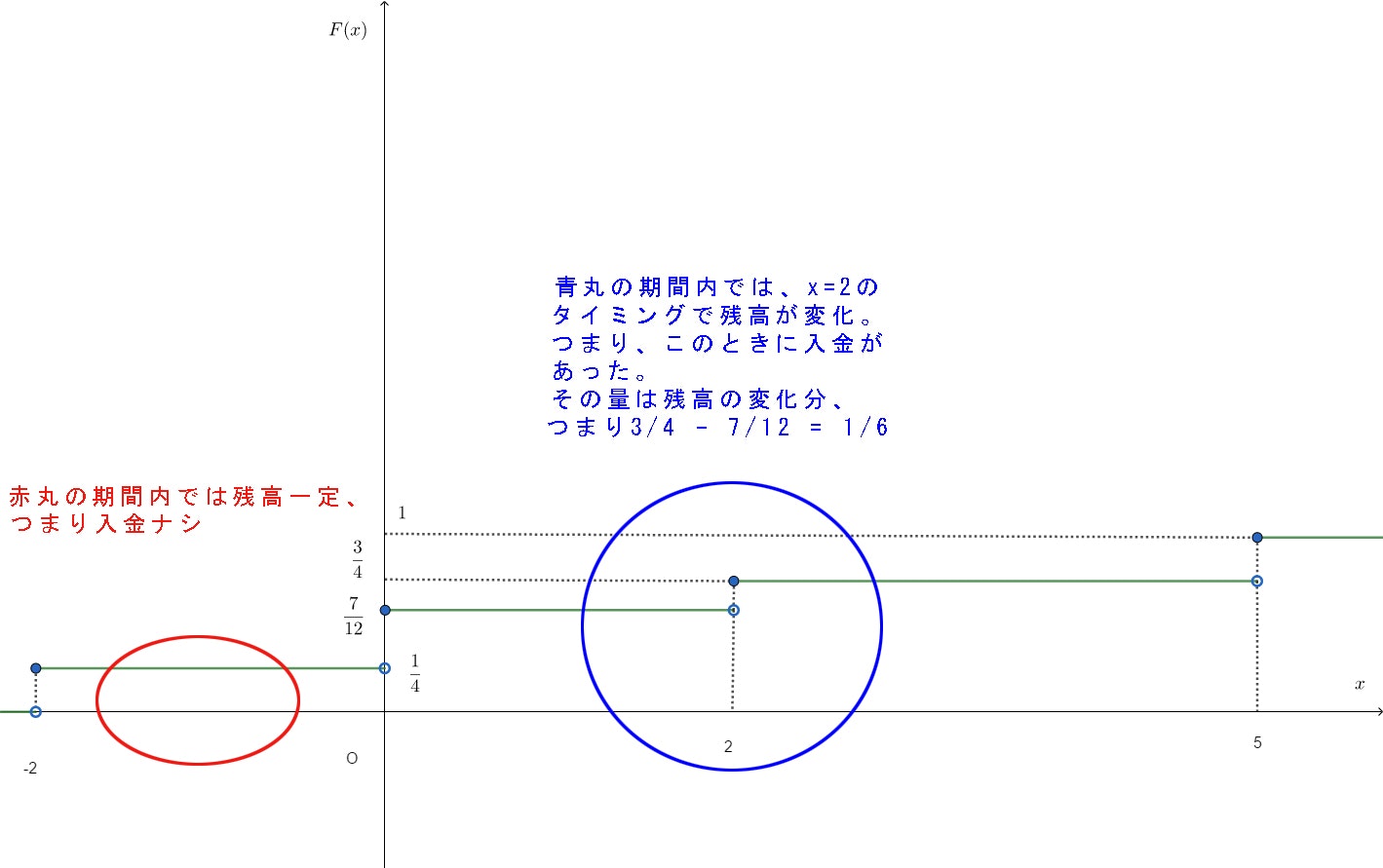
前述したように、離散型の累積分布関数を考える上で私がよく使う喩えは「入金専用の銀行口座の残高」です。つまり、お金が入ってくるだけ(出ることはない)の口座です。$x$は時間と考えます。まぁ、とりあえず$F(x)$のグラフを描いてみましょう。以下のようになります。
残高の喩えを使えば、横軸は時間、縦軸はそのときの残高です。$-2$「未満」の期間では残高0で一定ですからどのタイミングでも入金がないということです。しかし$-2$「以下」の期間ですとちょうど$-2$のときに残高が増えているので、$x=-2$のときに$\frac{1}{4}$の入金があったということです。
要するに注目している期間内でグラフがずっと一定ならば入金ナシ。逆にグラフに変化があれば、そのタイミングで入金があった(正の値の確率質量があった)ということです。入金額、すなわち確率質量の値は残高の変化分です。イメージ的には以下のようになります。
こんな感じで$F(x)$を横軸(時間軸)で追っていけば、入金のあったタイミングにそのときの入金額をプロットすれば確率質量関数$f(x)$が描けるというわけです。
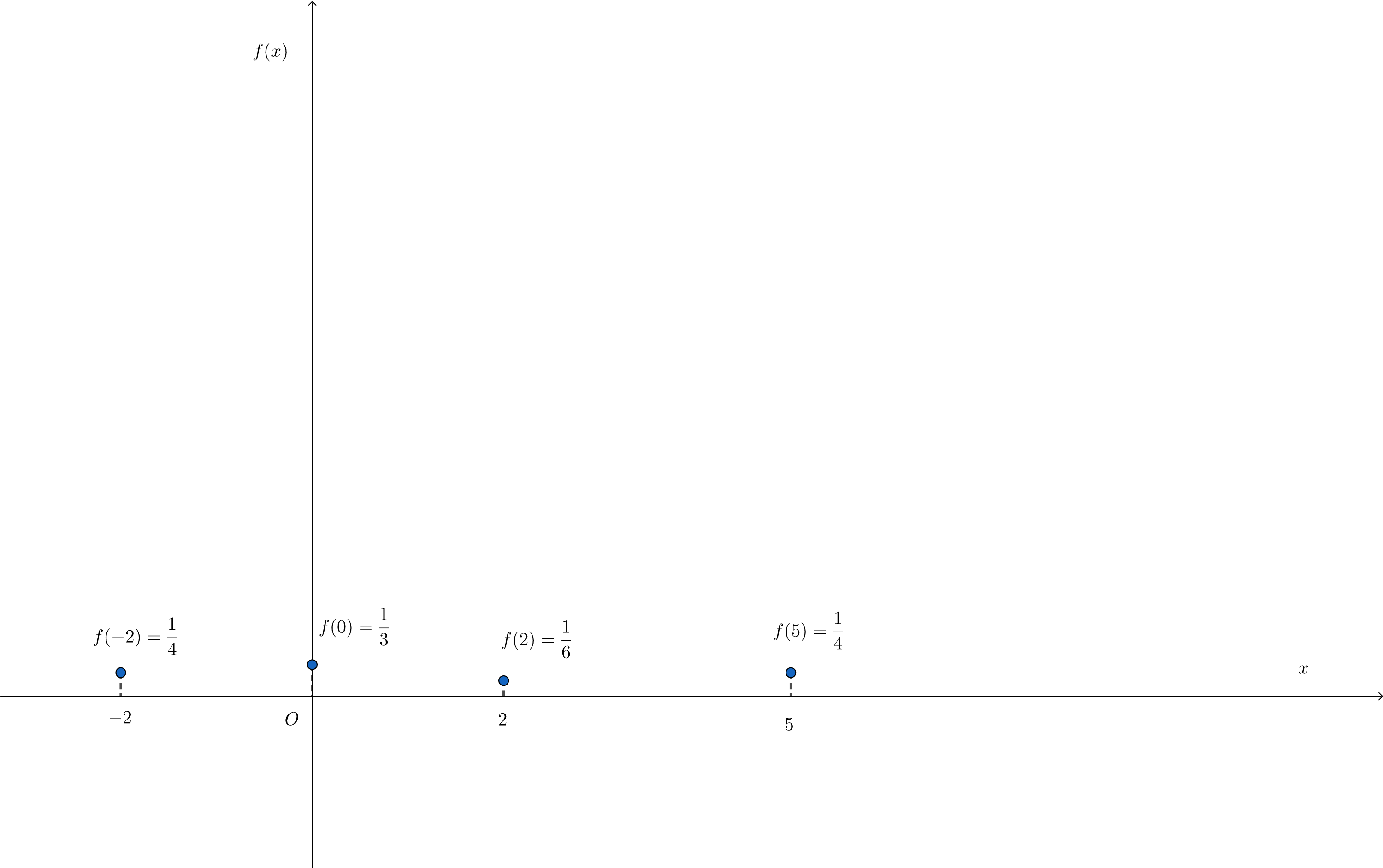
ということで入金のタイミングは4回あるのが分かると思いますので、それぞれの入金時での入金額を考えれば、確率質量関数$f(x)$のグラフは以下のようになります。
この$f(x)$の式は以下のようになります。
f(x) = \begin{cases}
\frac{1}{4} \hspace{1em} (x=-2,5)\\
\frac{1}{3} \hspace{1em} (x=0)\\
\frac{1}{6} \hspace{1em} (x=2)\\
0 \hspace{1em} (\mathrm{otherwise})
\end{cases}
確率$P(X \le -2)$、確率$P(-1 \le X \le 1)$、確率$P(X < 2)$、確率$P(3<X<4)$は累積分布関数$F(x)$を使って考えてもいいですし、確率質量関数$f(x)$を使って考えてもいいでしょう。このような例題だと個人的には$f(x)$をみた方が楽かな、という気はします。
$f(x)$のグラフをみて、$P(X \le -2)$は$-2$以下の期間での入金額$f(x)$をすべて足せばいいわけです。すると$x=-2$のところで$\frac{1}{4}$が1本あるだけですから$P(X \le -2)=\frac{1}{4}$となります。
$P(X < 2)$は$2$「未満」ですので2は含みません。ですから$f(x)$のグラフをみると、この期間で入金額があるのは$x=-2$のときの$\frac{1}{4}$と$x=0$のときの$\frac{1}{3}$ですので、これらを足して$P(X < 2)=\frac{7}{12}$となります。
$P(-1 \le X \le 1)$は、$-1$以上1以下の期間に注目します。すると、この期間で入金があるのは$x=0$のときの$\frac{1}{3}$です。よって、$P(-1 \le X \le 1)=\frac{1}{3}$となります。
$P(3< X < 4)$は、3より大きくて4未満の期間内に入金がないのは$f(x)$のグラフをみれば分かります。よって$P(3< X < 4)=0$です。
分散
データの特徴を表す指標として、平均と並んで重要なものが分散です。例えば、学校のクラスの平均点は確かにクラスの学力を特徴付ける量ですが、平均点付近の点数をとる生徒がほとんどおらず、二極化するような状況も十分ありえます。つまり言い方は悪いですが、成績下位の落ちこぼれ層と上位の優秀者層に分かれ、平均値はその中間の点ですが、そういう平均点付近をとる中間層が少ない(または下位層・上位層が中間層に比べて分厚い)ようなクラスです。
このような状況も考えると、平均値だけでは対象とする集団の特徴を捉える上で不十分と言えるでしょう。平均値付近にどのように各データ要素が散らばっているのか(あるいは集まっているのか)を表す指標も、データ全体の重要な特徴となるわけです。
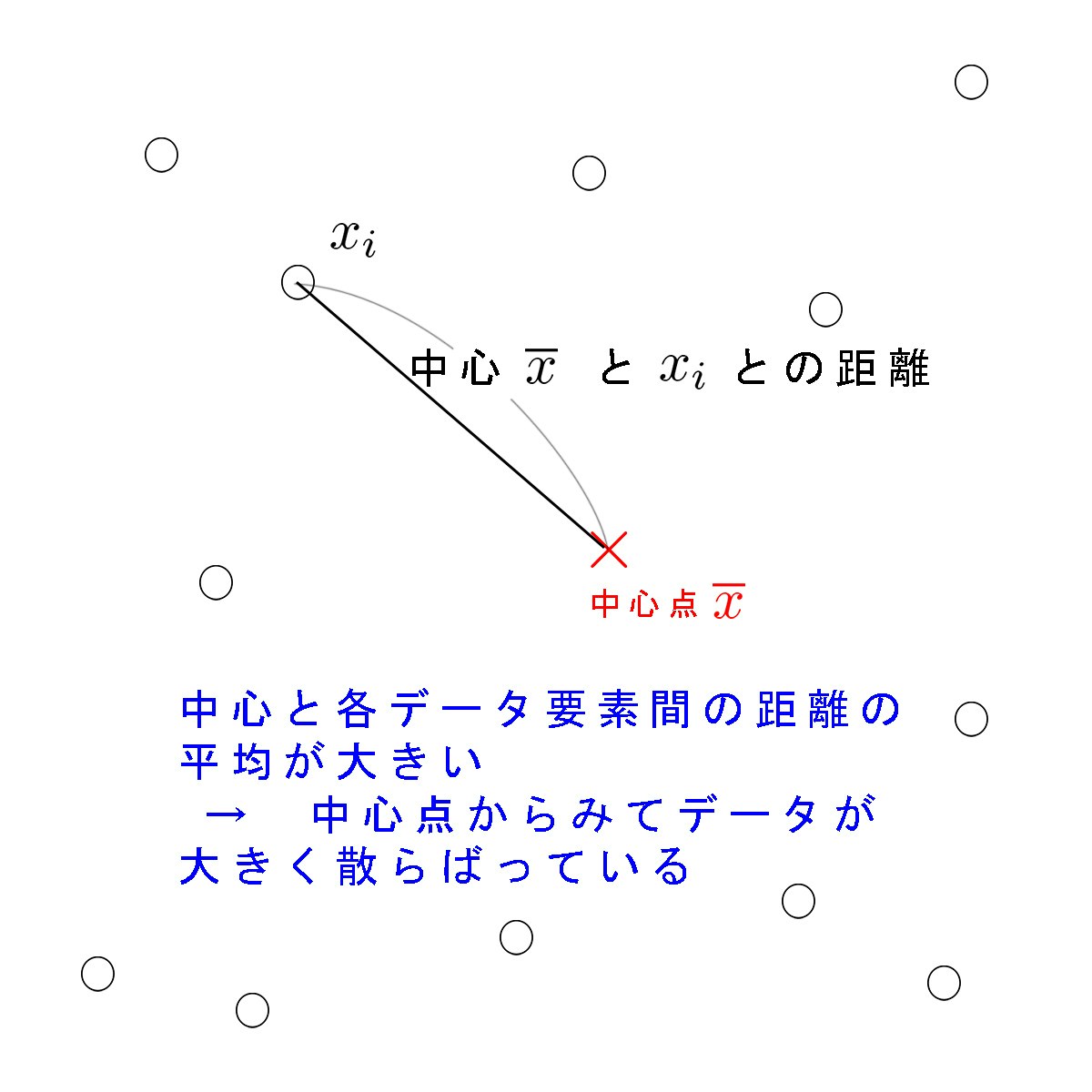
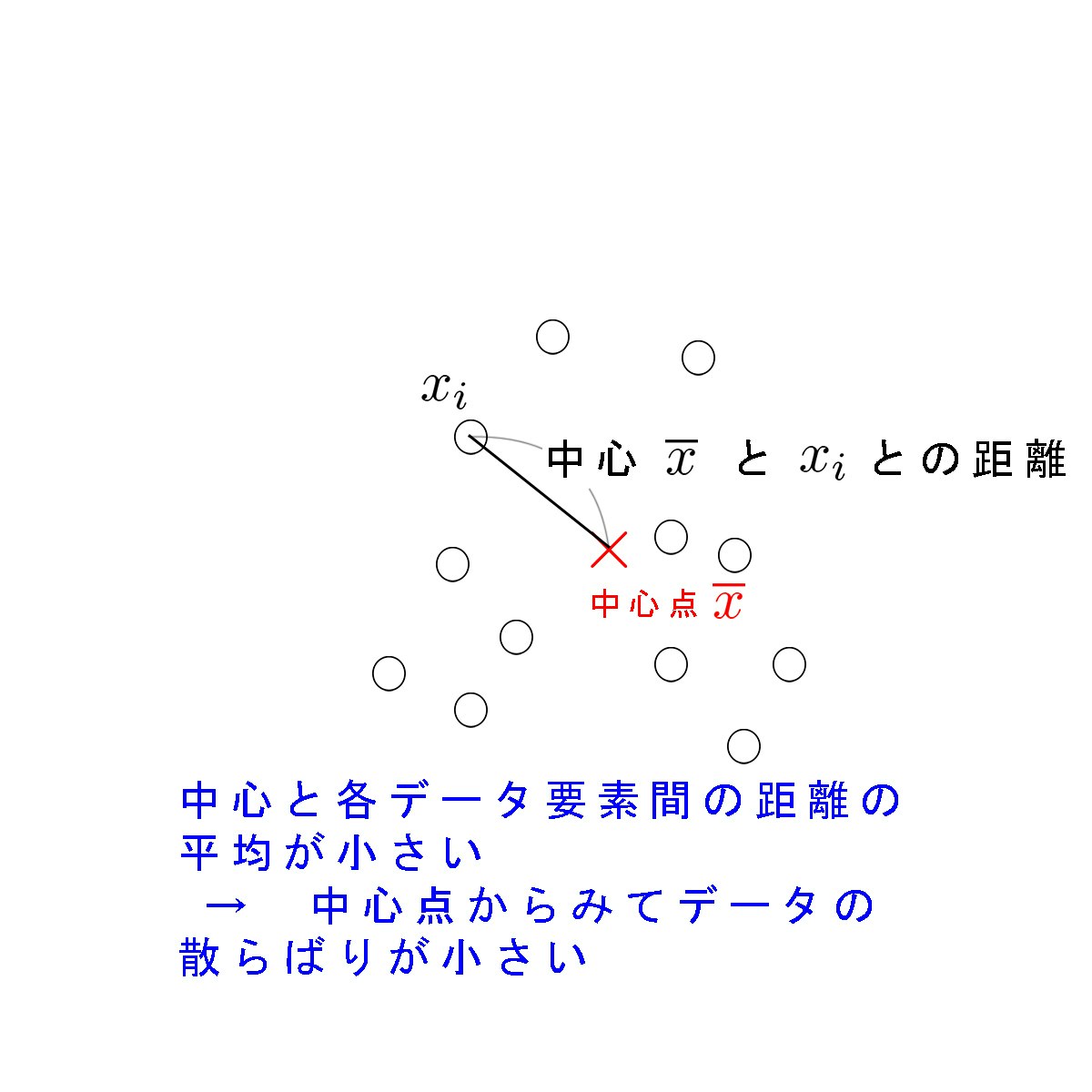
では、ものの散らばり具合が大きいとか小さいとか言うとき、人はどういうことを考えるのでしょうか?以下の2枚の図は、散らばり具合についての多くの人の直感と一致すると思います。
子どもが親に「散らかしたおもちゃを片付けなさい」と叱られるとき、親はおもちゃ箱などのあるべき場所(中心点)からはるか遠いところに多数のおもちゃがある、すなわち中心から各点の距離の平均が大きい様子を指して散らかると判断するということです。(もちろん、距離を強く意識することはないでしょうが)
あるいは散らばっている=対象とする各場所までの(平均的)距離が大きいというのを日常的に意識する別の喩えとして、次のような状況も挙げられるでしょう。仕事や趣味などで必要とする材料・道具類(例えば食材や食器類など)が作業場(キッチンの平らなところ)から離れているとき、「食材も包丁も皿も、キッチンから遠いところにあって散らばっているなあ…」と思う状況です。これは、必要とする物が中心とする場所よりおおむね離れている=平均的に遠いところにある、と感じる例だと思います。
分散の場合、中心点とするのはデータの平均値$\overline{x}= \sum_{i=1}^{n}x_i$です。平均値からみて、各データの要素がどの程度散らばっているのかを数値で表現したもの、すなわち平均値と各データ要素間の距離の平均が分散です。式と言葉で表すと次のようになります。
(分散と言えるもの) = \frac{1}{全データ数} \sum_{i=1}^{全データ数} (x_iと\overline{x}との距離)
ただし、「距離」と一言で表しても、世の中には様々な距離があります。(よく使う二点間距離はユークリッド距離と呼ばれますが、他にもマンハッタン距離や距離概念を一般化したミンコフスキー距離など様々…)これは平均と一言で表しても、算術平均もあれば前述したような期待値としての平均もあれば、幾何平均や調和平均などがあるのと似ています。
では、分散を計算する上ではどういった距離を用いるのがよいのでしょうか?
分散を計算するときの距離
正確に言うと数学的な距離の要件を満たしませんが、単に$x_i-\overline{x}$という、平均値と各データ要素の差を距離とみなすとどうなるでしょうか?つまり$\frac{1}{n} \sum_{i=1}^{n}(x_i - \overline{x}) $を分散とみなしたらどうなるでしょうか?
実はこれは次のように計算でき、常にゼロになってしまい、散らばりを表す尺度としては使いものになりません。
\begin{eqnarray*}
\frac{1}{n}\sum_{i=1}^{n}(x_i - \overline{x}) &=& \frac{1}{n}\left\{ \left( x_1 + x_2 + \ldots + x_n \right) - \underline{\left(\overline{x} + \overline{x} + \ldots + \overline{x} \right)} \right\} \hspace{1em} (下線部はn個の\overline{x}) \\
&=& \frac{1}{n}\left\{ \color{red}{\left( x_1 + x_2 + \ldots + x_n \right)} - n\overline{x} \right\} \\
&=& \frac{1}{n}\left\{ \color{red}{n\overline{x}} - n\overline{x} \right\} \\
&=& 0
\end{eqnarray*}
途中の赤文字のところは、平均の定義より$\frac{1}{n}\left( x_1 + x_2 + \ldots + x_n \right) = \overline{x}$だから、これに両辺$n$をかけると$\left( x_1 + x_2 + \ldots + x_n \right)=n\overline{x}$となることから成立します。
要するに$x_i-\overline{x}$を距離として分散計算することは、平均値どうしを引く計算に落ち着くので常にゼロになるわけです。
なお、冒頭の身長データでこの$x_i-\overline{x}$を距離として分散計算すると、小数の誤差からちょうどゼロにならなかった(もちろん、ほぼゼロと言ってよい小さい値になりますが)ので、以下のようにイイ感じに平均が整数値となるデータ列で試してみました。
tmp <- c(3,6,1,6,9)
sum(tmp - mean(tmp))/length(tmp)
$3,6,1,6,9$の平均値は5です。tmp - mean(tmp)で、元データ列の全ての要素から平均値5を引いた列、つまり$-2,1,-4,1,4$ができます。あとはその和をとり、データ数length(tmp)(つまり5個)で割るだけ。結果はゼロとなります。
では、中学数学で出る、数直線上の距離を表す絶対値を使うとどうでしょうか?つまり、$\frac{1}{n}\sum_{i=1}^{n}|x_i-\overline{x}|$を分散とするとどうでしょうか?
上記の$3,6,1,6,9$のデータ列でやってみましょう。コードは以下のようになります。
tmp <- c(3,6,1,6,9)
sum(abs(tmp - mean(tmp)))/length(tmp)
abs()でtmp - mean(tmp)の各要素の絶対値をとります。つまり$2,1,4,1,4$ができます。これをデータ数で割った値、つまり$x_i$と平均値$\overline{x}$の差の絶対値の平均は2.4と出力されます。
実は$\frac{1}{n}\sum_{i=1}^{n}|x_i-\overline{x}|$は統計学の世界では「〇〇分散」という名称ではなく、平均絶対偏差(mean absolute deviation: MAD)という用語があてられています。これは後述する分散のルート、つまり標準偏差のような偏差の一つとして使われます。
絶対値計算は中学・高校数学でやったように、場合分けをして外すことが一般的で、絶対値の個数が増えるほど外すのは大変な作業になります。それはプログラムの内部処理でも同様です。ですから、絶対値計算を行う平均絶対偏差は計算上の負荷が大きいのであまり使われない、という解説をするテキストもあるようです。ただ、現代では計算機の処理能力が上がっていますので、平均絶対偏差を使う場面も結構あるようです。
一般的によく使われる分散
一般的な分散は$(x_i - \overline{x})^2$を距離(いわゆる二乗距離)とする計算をします。つまり以下の式を分散とします。
分散: \ s^2 = \frac{1}{n} \sum_{i=1}^{n}(x_i - \overline{x})^2
二乗距離は二乗ですから0以上が保証され、また絶対値のように場合分けをする必要もないので比較的簡単に(人間がというより計算機が)計算できるものです。
先ほどの$3,6,1,6,9$のデータ列で分散を計算してみましょう。
tmp <- c(3,6,1,6,9)
(tmp - mean(tmp)) %*% (tmp - mean(tmp))/length(tmp)
この値は7.6となります。
また、冒頭の身長データでも同様に分散を計算してみましょう
data <- c(144.5, 165.8, 156.7, 146.2, 170.7,
172.4, 158.8, 153.1, 163.0, 166.2,
173.1, 142.9, 149.8, 157.6, 162.1,
168.9, 147.7, 157.8, 168.9, 170.2,
156.7, 163.8, 168.9, 169.7, 157.8,
159.7, 157.6, 179.5)
(data - mean(data)) %*% (data - mean(data))/length(data)
この値は85.49973となります。
不偏分散
ここで「そもそも論」を少し書きますが、統計調査は全数調査と標本調査に分けられます。全数調査の代表例は国勢調査で、これは5年に1度、日本国内の全世帯を対象に人口などのデータを集める大規模な調査です。当然、大きなコスト(モノ・カネ・ヒト・ジカン)がかかります。こうした全数調査はそう簡単に行えません。ですから、行政・民間・学術の世界を問わず、多くの統計調査は標本調査です。つまり、対象とする集団(母集団)から無作為にサンプルを抽出した集団(標本)の情報を調べるわけです。
母集団の知りたい性質をパラメータといいます。この母集団のパラメータは調査の内容や分析者の興味により様々なものがありえます。つまり、何かの平均値・中央値・分散・回帰係数・決定係数などなどです。
母集団のパラメータに対応するものが、サンプルの推定量です。つまり、サンプルにおける、何かの平均値・中央値・分散・回帰係数・決定係数などなどです。
重要なのは母集団のパラメータは固定された定数であるとみなされる点です。対して、サンプルの推定量は不確実な数、つまり確率変数とみなされます。例えば、世論調査で得られる結果は、サンプルによって変動することは容易に想像できるでしょう。また、こうした結果は実際にサンプルを抽出してみてはじめて分かるもの(実現値)です。
一例として、次のように170cmを平均値(また、後述する標準偏差は10)とする乱数(正規分布に従う乱数)を100個生成し、それを母集団 data2 としてみましょう。R では rnorm 関数を使えば簡単にこのような乱数を生成できます。
set.seed(7)
data2 <- rnorm(100, mean = 170, sd = 20)
なお、最初の set.seed(7) は乱数を生成するためのシード値で、ここに一定の値(今回は7)をセットすれば常に同じ乱数列が得られるようになり、実験・シミュレーションの再現性が保てます。
全部見せると無駄に行数をとるので一部だけとしますが、data2の中身は以下のようになります。
> data2
[1] 215.7449 146.0646 156.1141 161.7541 150.5865 151.0544 184.9628
[8] 167.6609 173.0532 213.7996 177.1397 224.3350 215.6290 176.4804
中略…
[92] 157.0915 182.3798 174.7279 186.9300 158.5271 192.3599 139.2000
[99] 161.2375 166.9865
言うまでもなく、母集団 data2 の平均値はrnorm関数で設定したように170です。この母集団から10個のサンプルを無作為に抽出します。これは sample 関数を使えば簡単に行えます。replace=TRUE とすると復元抽出、すなわち取り出したものが母集団に戻されるので、再びサンプリングするときに前回抽出した要素が再度選ばれることもありえるという状況になります。
s1 <- sample(data2,10,replace=TRUE)
このサンプルs1は次のようなデータになりました。
> s1
[1] 174.7279 158.5271 177.1397 147.8974 162.1315 192.3599 168.7520
[8] 150.5865 138.6426 172.0105
このs1というサンプルの平均値は mean(s1) で簡単に計算できます。その値は 164.2775 となりました。母集団の平均値170と比べると、微妙なところですね。なお、今回のやり方ですとサンプルのとり方には再現性がないので、人によって異なる値がサンプリングされると思います。
同様に別のサンプルs2を以下のように抽出してみましょう。
s2 <- sample(data2,10,replace=TRUE)
> s2
[1] 184.9628 215.6290 182.3798 178.6525 157.6883 143.7689 194.3710
[8] 192.1850 192.3599 173.6839
s2の平均値は 181.5681 となりました。
当然と言えば当然ですが、サンプルによって平均値が異なりました。つまりブレがあるわけです。これはサンプルを抽出する行為にランダム性があり、毎回同じサンプルをとるわけではないためで、サンプルの推定量(この場合は平均値)が確率変数であることの分かりやすい例と言えるでしょう。
統計調査を行う人・利用する人にとっては当然の要望でしょうが、標本調査で得られる推定量は、母集団のパラメータになるべく一致してほしいわけです。サンプル数を増やしていくほど母集団のパラメータに一致していくような推定量を一致推定量といいます。これは望ましい推定量が持つ性質の一つと言えるでしょう。
また、サンプルの推定量は確率変数であると書きました。実際にRでシミュレートしたように、確率変数である推定量は相異なるサンプルによってブレます。ですから、確率的な立場からみると推定量の期待値(確率的な平均値)が重要な意味を持ちます。確率変数である推定量の期待値が母集団のパラメータと等しいことが、統計調査を行う人・利用する人にとってやはり望ましい性質です。このように、期待値が母集団のパラメータと等しい推定量を不偏推定量といいます
一致性・不偏性とも、詳しくは別の記事で書こうかと思いますが、実は$s^2 = \frac{1}{n} \sum_{i=1}^{n}(x_i - \overline{x})^2$という分散は一致性はありますが不偏性がありません。しかし、$\frac{1}{n}$を$\frac{1}{n-1}$にすると不偏性を持ちます。これを不偏分散といいます。
不偏分散: \ s^2 = \frac{1}{n-1} \sum_{i=1}^{n}(x_i - \overline{x})^2
不偏分散と分散でどのくらい違いが出るのか
結論から言えば、不偏分散と分散で、ほとんど値に違いは出ません。
以下、身長データの母集団を1千万(平均は170、標準偏差は20、すなわち分散400)として、ここから10回サンプルをとるプログラムを示します。サンプルサイズ(sample_size)は最初は100としていますが、1000、10000、100000と大きくしていきます。
v1が10個のサンプルセットの各分散値を格納したベクトル、v2は不偏分散値を格納したベクトルです。
set.seed(7)
data3 <- rnorm(10000000, mean = 170, sd = 20)
num_of_samples = 10 # サンプル数
sample_size = 100 # サンプルサイズ
# サンプル格納用の行列
s <- matrix(numeric(num_of_samples*sample_size),
nrow = num_of_samples, ncol = sample_size)
# 各行の分散値格納用のベクトル
v1 <- numeric(num_of_samples)
# 各行の不偏分散値格納用のベクトル
v2 <- numeric(num_of_samples)
for(i in 1:num_of_samples){
s[i,] <- sample(data3, sample_size,replace=TRUE)
v1[i] = ((s[i,] - mean(s[i,])) %*% (s[i,] - mean(s[i,])))/length(s[i,])
v2[i] = ((s[i,] - mean(s[i,])) %*% (s[i,] - mean(s[i,])))/(length(s[i,])-1)
}
サンプルサイズ100のときの分散v1、不偏分散v2は以下の通りです。
> v1
[1] 438.6943 426.0947 350.2167 481.8827 363.1216 352.9944 323.3190
[8] 310.5357 325.9828 444.3589
> v2
[1] 443.1256 430.3987 353.7543 486.7502 366.7895 356.5600 326.5848
[8] 313.6725 329.2756 448.8474
途中は省略しますが、サンプルサイズを1000、10000、100000と大きくしていきます。100000のときの分散v1、不偏分散v2は以下の通りです。
> v1
[1] 399.9563 401.0091 398.4586 399.9287 400.1097 399.2259 398.1390
[8] 397.1679 401.2981 399.7672
> v2
[1] 399.9603 401.0132 398.4626 399.9327 400.1137 399.2299 398.1430
[8] 397.1718 401.3021 399.7712
サンプルサイズが100のときは母集団の分散である400からけっこう外れた値もありますが、サンプルサイズを大きくするにつれ、400に近づいているのは分かると思います。しかし、これを見て分散と不偏分散の違いを感覚的に分かる人はいないでしょう。
ですから実用上は大した差はありませんが、理論的には不偏推定量である不偏分散を使うべき、ということを理解すれば今の段階では十分だと思います。
標準偏差
分散はデータの散らばりを表す指標としては二乗距離を使うので計算も比較的しやすいのですが、単位が元データと異なります。身長データですと平均値の単位は$cm$ですが、分散の単位は$cm^2$となり、両者を比較することが困難です。
そこで、分散のルートをとって元データと単位を揃えた尺度にします。これを標準偏差といいます。式は次の通りです。
標準偏差: \ s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n}(x_i - \overline{x})^2}
なお、前述した平均絶対偏差$\frac{1}{n}\sum_{i=1}^{n}|x_i-\overline{x}|$も、1乗の値ですから元データと同じ単位です。ですから「偏差」という言葉が当てられるのが適当と思われます。
おまけ: 中央値を横軸、相対度数を縦軸にとるグラフ
ヒストグラムの階級幅を小さくしていくと確率密度関数の概形に近いものが得られると書きました。そこで、上記の1千万個の身長データを利用して、横軸に中央値、縦軸に相対度数(便宜上、密度と考えてよいもの)をとったグラフを出力してみましょう。
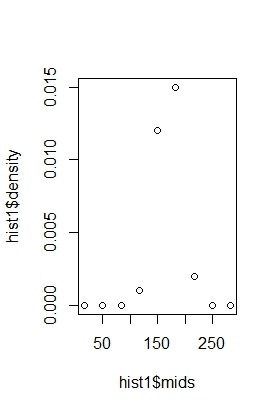
まずは、階級を10個に区切ったものを出力してみましょう。以下のコードを実行します。
hist1 <- hist(data3, breaks = seq(0, 300, length=10))
plot(hist1$mids, hist1$density)
このグラフは次のようになります。
どうでしょうか?まだ確率密度関数の概形は見えてこないと思います。
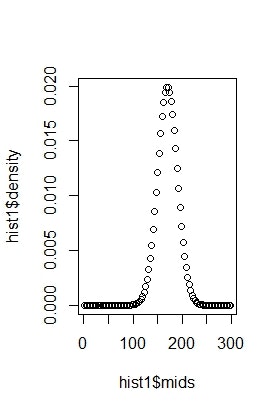
上記コードの length を100に増やしてみましょう。つまり、階級を100個に区切ってみます。すると以下のようなグラフが出力されます。
身長170cmを平均値とする山があるのが見えてきたと思います。もともと、170を平均値とする正規分布から生成した乱数ですので、このような形(確率密度関数の概形)となります。
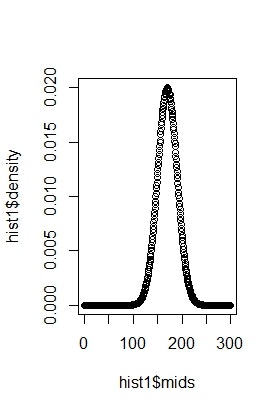
さらに length を500に増やしてみましょう。以下のようなグラフになります。
別の記事で書くと思いますが、まさに正規分布する確率変数の確率密度関数の概形とほぼ一致していると思います。
階級を細かく区切る、すなわち階級幅を小さくしていくと相対度数のグラフが確率密度関数の概形に近づくというのが感覚的に理解できると思います。
続きについて
と、ここまで記事を更新しならがら書いていきましたが、そろそろ度数分布まわりのことから離れて、統計学の概論・基礎論とでも言うべき内容になってきました。ということで、これ以降の内容、例えば二項分布やポアソン分布、正規分布などに代表されるよく使う確率分布のことや、t検定やカイ二乗検定などの推定・検定まわりのこと、そして回帰などのことは別記事で書いていこうかと思いますので、今回はここまでということで。
-
私は在籍していないのでよくは知りませんが、慶應の通信課程というのは世間一般的に思う通信教育、つまりテキストやらを買って自宅などで自習し、レポート等を出して単位をとるテキスト授業と、今回のように慶應のキャンパス(日吉または三田)へ通って授業に出席するスクーリング授業(普通の全日制学部でいうところの集中講義的なやつ)に分かれるようです。そして、テキスト授業の「統計学」とスクーリング授業の「統計学」の両方は別々の単位として認定される(編入に当たる学士入学の人とかは条件が異なるようですが)ようです。カミさんはまだテキスト授業の統計学(カミさんの在籍する経済学部はテキスト授業の統計学が必修)をとっていませんが、その必修の単位の予習としてスクーリング授業の統計学を今回とったという経緯があります。まあ、予習というのは格好つけた言い方で、じつのところ私が「ド素人状態だと予習にすらならないと思うが、単位をワンチャン狙いでとってみろ」とそそのかしたという背景もありますが… ↩
-
もちろん、経済学の立場から統計学とその周辺を真面目にやるならば計量経済学の諸テキスト(ウルドリッジの分厚い本とか林の難しい本とか)をやる必要があるでしょうし、情報工学の立場からだと機械学習のテキスト(例えばビショップの黄色い上下巻本とか)をやる必要があるでしょうし、基礎となる確率論もルベーグ積分論から追っていく必要があるでしょうが、そんなことはここではやりません。 ↩
-
ちなみに、この説明では世間の常識的に「密度」というと「体積密度」を指すことから若干回りくどい説明をしましたが、物理などで使用する面密度・線密度の積分概念を使えばもっとイメージしやすいと思います。…が、そういう線密度・面密度を使う人はここら辺の確率密度関数の理解は大丈夫だと思いますが… ↩
-
面積も体積も質量も測度論では非負値性とσ-加法性を持つ集合関数として一般化されますが、これに全測度が1になる条件が加わった測度を確率測度とします。ですから面積とか体積とか質量のアナロジーで確率を捉えることは測度論の立場からみるとお薦めの理解だと思います。 ↩