はじめに
ゼロから作るDeep Learning①第7章の中で、深堀した内容をまとめます。
個人的にこれらを通じて理解が深まったので、少しでも皆さんのお役にも立てたらと思います。
※本の内容を補足するような形なので、1から解説するような内容では無い点ご了承ください。
7.2.4 ストライド(p.211)
出力データのサイズは以下のように計算されます。
OH = \frac{H + 2P - FH}{S} + 1 \\
OW = \frac{W + 2P - FW}{S} + 1
そこで、どうしてこの計算式で出力データサイズが出るのか考えてみた結果を図解したいと思います。
前提として、OH,OWともに同様の式で算出されるため、今回は幅のOWのみに着目します。
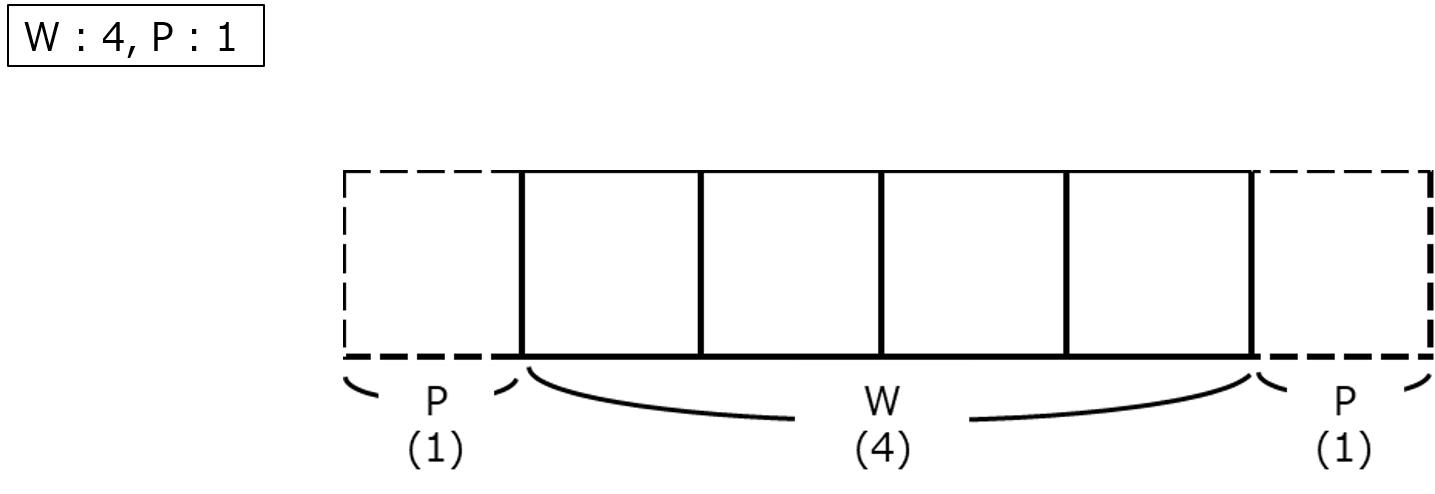
①まず、$OW = \frac{W + 2P - FW}{S} + 1$ の$W+2P$はパディング後のデータの列数を表しています。
例えば幅(W)が4、パディング(P)が1の時、列数は下図のように$4 + 2×1=6$ となります。
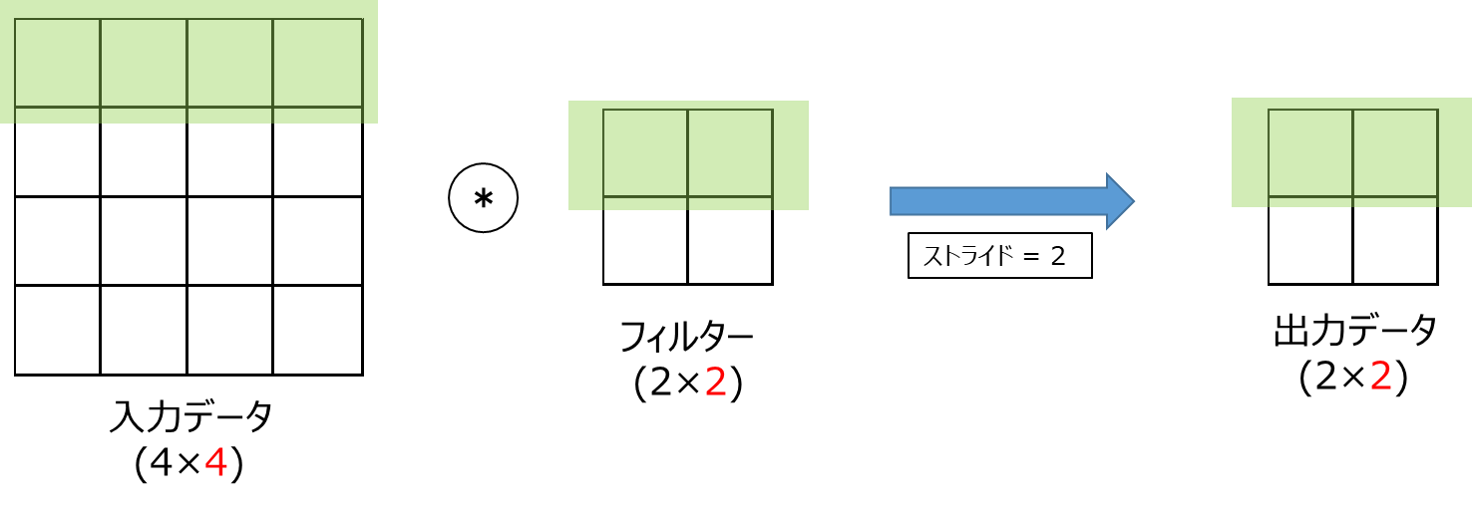
②次に、$OW = \frac{W + 2P - FW}{S} + 1$の$W+2P-FW$はフィルターを重ねた時の残りの列数を表しています。
下図の例だと、フィルターを重ねた残りの列数は$4 + 2×1 - 2 = 4$となります。

③$OW = \frac{W + 2P - FW}{S} + 1$の$\frac{W + 2P - FW}{S}$はフィルターを何回分動かすかを表します。
下図の例だと、
$W+2P-FW = 4$
$S = 2$
なので、$4 / 2 = 2$回分を動かしています。

④最後に、$OW = \frac{W + 2P - FW}{S} + 1$の $+1$は、OWに1足りない分です。
(Ex. 2回動かした場合はOW=3となる)

以上が、ストライドの計算式の図解になります。
7.4.2 im2colによる展開(p.222)
計算例
im2colを含むConvolutionレイヤの具体的な計算例についてです。
例えば、
入力データサイズ = (1,3,3,3)
フィルターサイズ = (3,3,1,1)
この場合に、各過程でそれぞれのサイズがどのように変化しているのかを図示してみました。

fはim2col後の入力データの行数です。1つの入力データに対してのフィルターの適用回数(OH×OW)×Nで計算されます。そのため、今回は3×3×1 = 9です。
次でもう少し詳しく解説します。
im2col後の行数(f)について
入力データへのフィルターの適用回数によってim2col後の行数(f)は変化します。
例えば下図のように、
9回適用する場合はf = 9 × N
4回適用する場合はf = 4 × N
となります。

今回はN = 1(入力データのバッチサイズが1)としているため、fはそれぞれ9と4になります。
7.4.3 Convolutionレイヤの実装(p.224)
下記はConvolutionレイヤの実装コードです。
この中の、
#深堀ポイント1
col_W = self.W.reshape(FN, -1).T
#深堀ポイント2
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
この2点について、図解したいと思います。
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
#深堀ポイント1
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
#深堀ポイント2
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out
深堀ポイント1 : col_W = self.W.reshape(FN, -1).Tについて
一見すると、
col_W = self.W.reshape(-1, FN)
でも形状が一緒になるので良いのでは無いかと思いました。
しかし、結論から言うとそれでは結果の出力が変わってしまいます。
例えば、
フィルターサイズ = (2,3,1,1)
のフィルターを、
①self.W.reshape(FN(2), -1).T
②self.W.reshape(-1, FN(2))
の2通りでreshapeしてみるとどうなるのか、図で見てみます。

図のように、同じ形状でも結果が異なってしまいます。
なので、
col_W = self.W.reshape(FN, -1).T
を
col_W = self.W.reshape(-1, FN)
と書いてはいけない、という事になります。
深堀ポイント2 : out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)について
ここでの処理を可視化してみました。
例えば、
出力データサイズ = (2,2,2,3)
のデータに対して
transpose(0, 3, 1, 2)
をすると、図のように変形されます。

これは、下図のように、12個からなるそれぞれのボックスを
①x軸→y軸方向に90°
②y軸→z軸方向に-90°
とくるくる回転させるイメージです。

7.4.4 Poolingレイヤの実装(p.227)
計算例
Poolingレイヤの具体的な計算例についてです。
例えば、
入力データサイズ = (1,3,6,6)
プーリングウィンドウサイズ = (2,2)
この場合に、各過程でそれぞれのサイズがどのように変化しているのかを図示してみました。

pはim2col後の入力データの行数です。
1つの入力データに対してのウィンドウの適用回数(OH×OW)×Nで計算されます。
そのため、今回は3×3×1 = 9です。
誤植?
下記コードは、p.228図7-21の数値を元にした実装コードです。
from common.util import im2col
first = np.array([[1,2,3,0], [0,1,2,4],[1,0,4,2],[3,2,0,1]])
second = np.array([[3,0,6,5],[4,2,4,3],[3,0,1,0],[2,3,3,1]])
third = np.array([[4,2,1,2],[0,1,0,4],[3,0,6,2],[4,2,4,5]])
x = np.stack([first, second, third], axis = 0)
x = x[np.newaxis, :, :]
N, C, H, W = x.shape
pool_h, pool_w = 2,2
out_h, out_w = 2,2
col = im2col(x, pool_h, pool_w, 2, 0)
col = col.reshape(-1,pool_h * pool_w)
print(col)
out = np.max(col, axis = 1)
out = out.reshape(N, out_h, out_w, C).transpose(0,3,1,2)
ですが、こちらのprint(col)で出力される内容が、以下のように教科書と異なってしまっています。
(最後のoutの結果は同じです。)

もしかしたら誤植かも知れないと思いますが、もし自分の実装や理解が違うようでしたら、ぜひコメントでご指摘頂けると幸いです。
終わりに
こちらの本はディープラーニングの実装だけでなく、仕組みについても一から深く理解する事が出来るため非常におすすめです。
②の自然言語処理編にも取り組んでみたいと思います。