自動車の燃費予測

目次

1.はじめに
2.データ概要
3.前処理
4.EDA
5.モデル構築
6.まとめ
7.参考

1.はじめに

今回、データ分析の練習としてsignateに挑戦しました。signateとは日本版kaggleのような形で、データ分析コンペを実施しています。
その中で今回は「自動車の走行距離予測モデルの作成」に挑戦した経過を記事にしました。

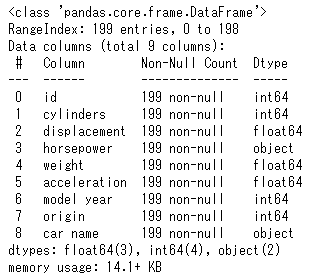
2.データ概要

trainデータ
→説明変数：8、サンプルデータ数：199

testデータ
→説明変数：7、サンプルデータ数：199

3.前処理

欠損値は図1でないと確認したものの、説明変数の一つ（horsepower)に「？」があることを確認する。

horsepowerとorigin、cylindersとの関係から

# 欠損値（？）をシリンダーとoriginでグループ化した後のグループ内で平均をとり埋める
def preprocessing(df):
    
    df['horsepower'] = df['horsepower'].replace('?','-9999.0')
    
    df['horsepower'] = df['horsepower'].astype('float')
    
    df.horsepower[df['horsepower'] <= 0] = df[df['horsepower'] <= 0].apply(lambda x:df.query('horsepower > 0').groupby(['cylinders','origin']).horsepower.mean()[x.cylinders][x.origin],axis=1)
    
    return df

horsepowerのデータ型をobject型からfloat型に変換。

4.EDA

説明変数間の相関関係を確認する。

各変数の特徴をリスト化

'mpg':目的変数

'cilinders':4,6の燃費が良い、メーカー（car name）も一緒に確認

'displacement':少ないほうが燃費がいい

'horsepower':欠損値あり（？）、object⇒float変換、分布確認

'weight':物理の公式上、理論上に比例関係を持つ

'acceleration':あまり関係ない？

'model year':80年代以降が燃費良い、時代背景ある？

'origin':1:アメリカ（燃費が良くない）、2:ヨーロッパ、3:日本（燃費良い）

'car name':dieselがかなり燃費良い（変数追加の案）、originを参照

その他散布図や棒グラフはGit(https://github.com/hirokisugino1/signate01.git)
にて確認お願いします。

モデル構築

ひとまず回帰分析としてRidge回帰とLasso回帰を行う。

Ridge回帰

from sklearn.linear_model import Ridge
from sklearn import metrics
# Ridgeクラスの初期化
ridge = Ridge()

# 学習の実行
ridge.fit(X_train, y_train)

# 訓練データの正解率
train_score_ridge = format(ridge.score(X_train, y_train))
print('リッジ回帰の正解率(train):', 
      '{:.6f}'.format(float(train_score_ridge)))

# テストデータの正解率
test_score_ridge = format(ridge.score(X_test, y_test))
print('リッジ回帰の正解率(test):', 
      '{:.6f}'.format(float(test_score_ridge)))

y_pred2 = ridge.predict(X_test)

MAE  = metrics.mean_absolute_error(y_test, y_pred2)  #--  MAEの算出
RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred2)) #-- RMSEの算出

print('MAE:',MAE)
print('RMSE:',RMSE)

出力結果
リッジ回帰の正解率(train): 0.823564
リッジ回帰の正解率(test): 0.810783
MAE: 2.2895358845862983
RMSE: 3.01127976441219

ラッソ回帰

from sklearn.linear_model import Lasso
#lassoクラス
lasso = Lasso(alpha=1)
#学習の実行
las = lasso.fit(X_train,y_train)

#訓練データの正解率
train_score_lasso = format(lasso.score(X_train,y_train))
print('ラッソ回帰の正解率（train）:',
     '{:.6f}'.format(float(train_score_lasso)))

#テストデータの正解率
test_score_lasso2 = format(lasso.score(X_test,y_test))
print('ラッソ回帰の正解率（test）:',
     '{:.6f}'.format(float(test_score_lasso2)))

y_pred5 = las.predict(X_test)

MAE  = metrics.mean_absolute_error(y_test, y_pred5)  #--  MAEの算出
RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred5)) #-- RMSEの算出

print('MAE:',MAE)
print('RMSE:',RMSE)

出力結果
ラッソ回帰の正解率（train）: 0.789607
ラッソ回帰の正解率（test）: 0.759556
MAE: 2.6763810418400364
RMSE: 3.394524641333855

あまり精度がいいとは言えなさそうですね。
現時点でも高精度であるlightGBMを用いてみます。

lightGBM(simple)

#ハイパーパラメータ調整なし
lgb_reg=lgb.LGBMRegressor()
lgb_reg.fit(x_train, y_train)

pred10=lgb_reg.predict(x_train)
pred11=lgb_reg.predict(x_test)

print('学習用：', np.sqrt(mean_squared_error(y_true=y_train, y_pred=pred10)))
print('検証用：', np.sqrt(mean_squared_error(y_true=y_test, y_pred=pred11)))

出力結果
学習用： 2.2293780535257546
検証用： 2.406105826615443

なかなかよさそうです。
ハイパーパラメータの調整のためにグリッドサーチを試します。

from sklearn.model_selection import GridSearchCV

lgb_reg5=lgb.LGBMRegressor()

params={
    'max_depth':[i for i in range(1,5)],
    'num_leaves':[2**i for i in range(1,5)],
    'learning_rate':[0.05+0.01*i for i in range(1,10)]
}

grid = GridSearchCV(
    estimator=lgb_reg2,
    param_grid=params,
    cv=10,
    scoring='neg_mean_absolute_error',
    verbose=10
)

grid.fit(x_train,y_train)

print('最適なハイパーパラメータ',grid.best_params_)

最適なハイパーパラメータ {'learning_rate': 0.12, 'max_depth': 3, 'num_leaves': 4}

このパラメータを用いて、

best_params_ = grid.best_params_
lgb_reg5=lgb.LGBMRegressor(
    max_depth=best_params_['max_depth'],
    num_leaves=best_params_['num_leaves'],
    learning_rate=best_params_['learning_rate']
)

lgb_reg5.fit(x_train,y_train)

pred_train=lgb_reg5.predict(x_train)
pred_test=lgb_reg5.predict(x_test)

#グリッドサーチmax_depth:3,num_leaves:4,learning_rate:0.07
print('学習用：',np.sqrt(mean_squared_error(y_train,pred_train)))
print('検証用：',np.sqrt(mean_squared_error(y_test,pred_test)))

出力結果
学習用： 2.004581456277775
検証用： 2.766871865157943

いい感じです。
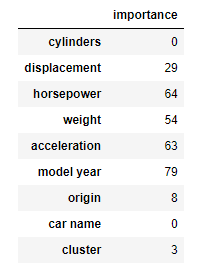
ここで特徴量重要度を確認してみましょう。

#特徴量の重要度を確認
importance = pd.DataFrame(lgb_reg5.feature_importances_, index=x_train.columns, columns=['importance'])
display(importance)

出力結果

これだけを見ると加速度とモデル年が大きな影響を与えていることがわかる。
EDAと比べて加速度が大きな影響を与えるとは思わず、差を発見することとなった。
そこで、教師無し学習からクラスタリングを用いてデータの性質を調べてみる。

#階層的クラスタリング
X = df_train.drop(['id','mpg','car name'],axis=1)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

result = linkage(X_scaled,method='ward')

"""
single:最小距離法
complete:最長距離法
centroid:重心法
ward:ウォード法
"""
#デンドログラム
dendrogram(result)
plt.figure(figsize=(12,8))
plt.show()

出力結果

この結果から車の性能がcylinderと重さで説明できることが判明する。
このクラスターを変数に加えてグリッドサーチしてみる。
そうすると
結果
学習用： 2.1676492699287015
検証用： 2.6752231300005573

この結果から少ししか新たに追加した変数は結果に寄与しなかったことがわかった。

その他、optunaを用いてlightGBMを試行したり、Adaboostを試行したりしたため、まとめの後にコードを載せておく。

6.まとめ

今回は特徴量に対しての情報が少ない状態からスタートしたことから、特徴量の把握に時間を擁した。特に、originの特徴把握ではcar nameやhorsepowerといった他の特徴量の関係から、法則を導き出した。ドメイン知識の有無も特徴量理解にも影響することから、EDAとともにドメイン知識のインプットも重要であると感じた。

モデルに関してはoptunaを使いこなすことができればスコアが良くなると感じた。また、signateに対する提出スコアは後にコードを出すAdaboostがもっとも良かった。訓練データに対して過学習を起こしていたにもかかわらずスコアが良かったため、この要因も追及できればと思う。

車、バイク好きの私からすると非常に興味深い内容でした。
コンペの練習としてお勧めします。

7.参考

AdaBoost

from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor

model = AdaBoostRegressor(n_estimators=1000,
                         random_state = 0,
                         base_estimator = DecisionTreeRegressor(random_state = 0,
                                                               max_depth=6))

model.fit(x_train,y_train)#学習


print(model.score(x_test,y_test))

lightGBM+optuna

import optuna.integration.lightgbm as lgbo

train=lgb.Dataset(x_train, y_train)
test=lgb.Dataset(x_test, y_test)

params = {
    "objective": "regression_l2",
    "metric": "mean_squared_error",
    'n_estimators': 100000, 
    'verbosity':-1,
    'n_jobs':-1
}

lgbo1 = lgbo.train(params, train, 
                    valid_sets=test,
                    verbose_eval=False,
                    early_stopping_rounds=1000,
                    )


print('学習用：　',mean_squared_error(y_pred=lgbo1.predict(x_train),y_true=y_train, squared=False))
print('検証用：　',mean_squared_error(y_pred=lgbo1.predict(x_test),y_true=y_test,squared=False))