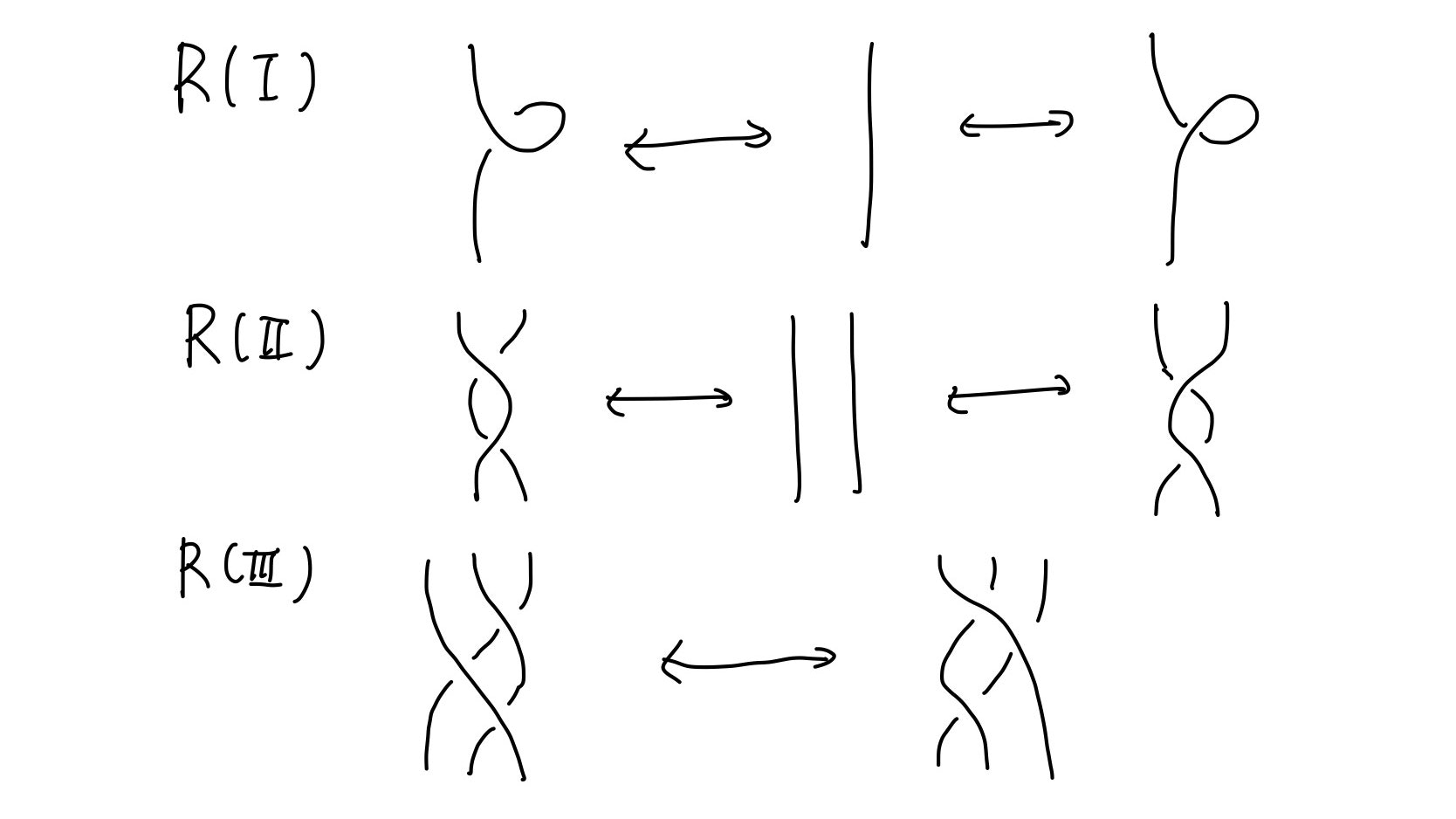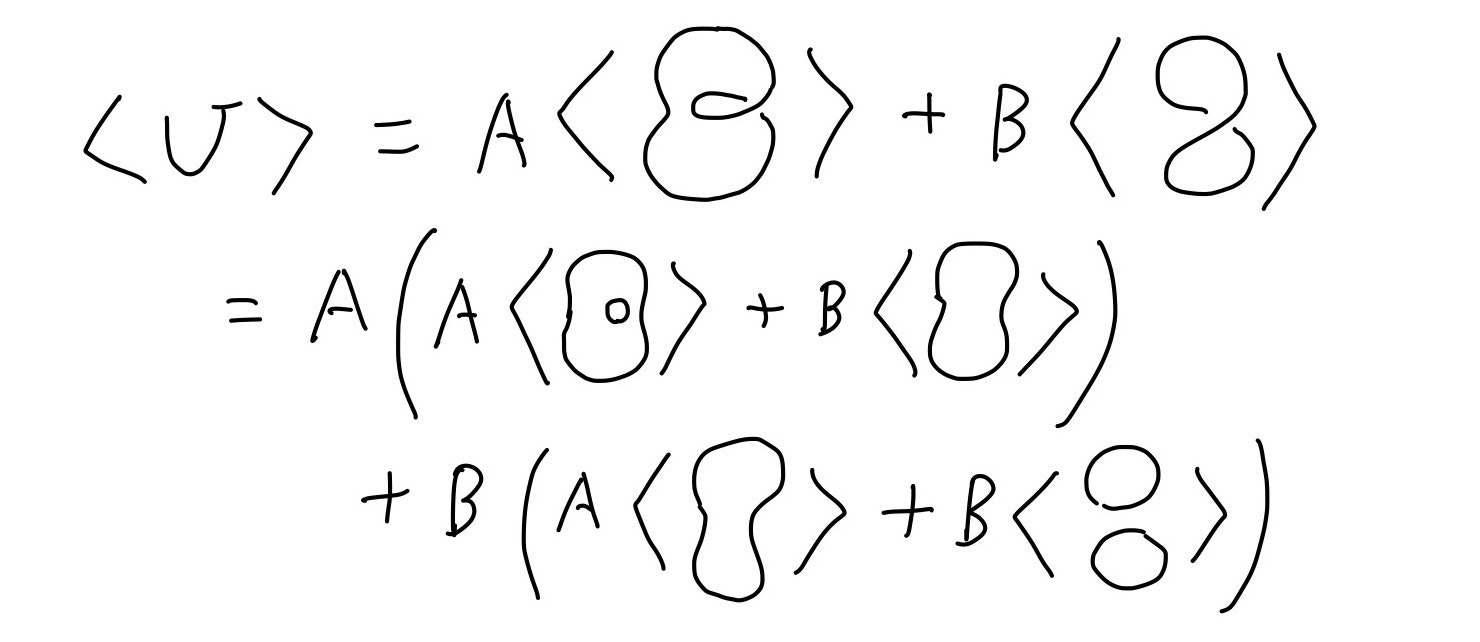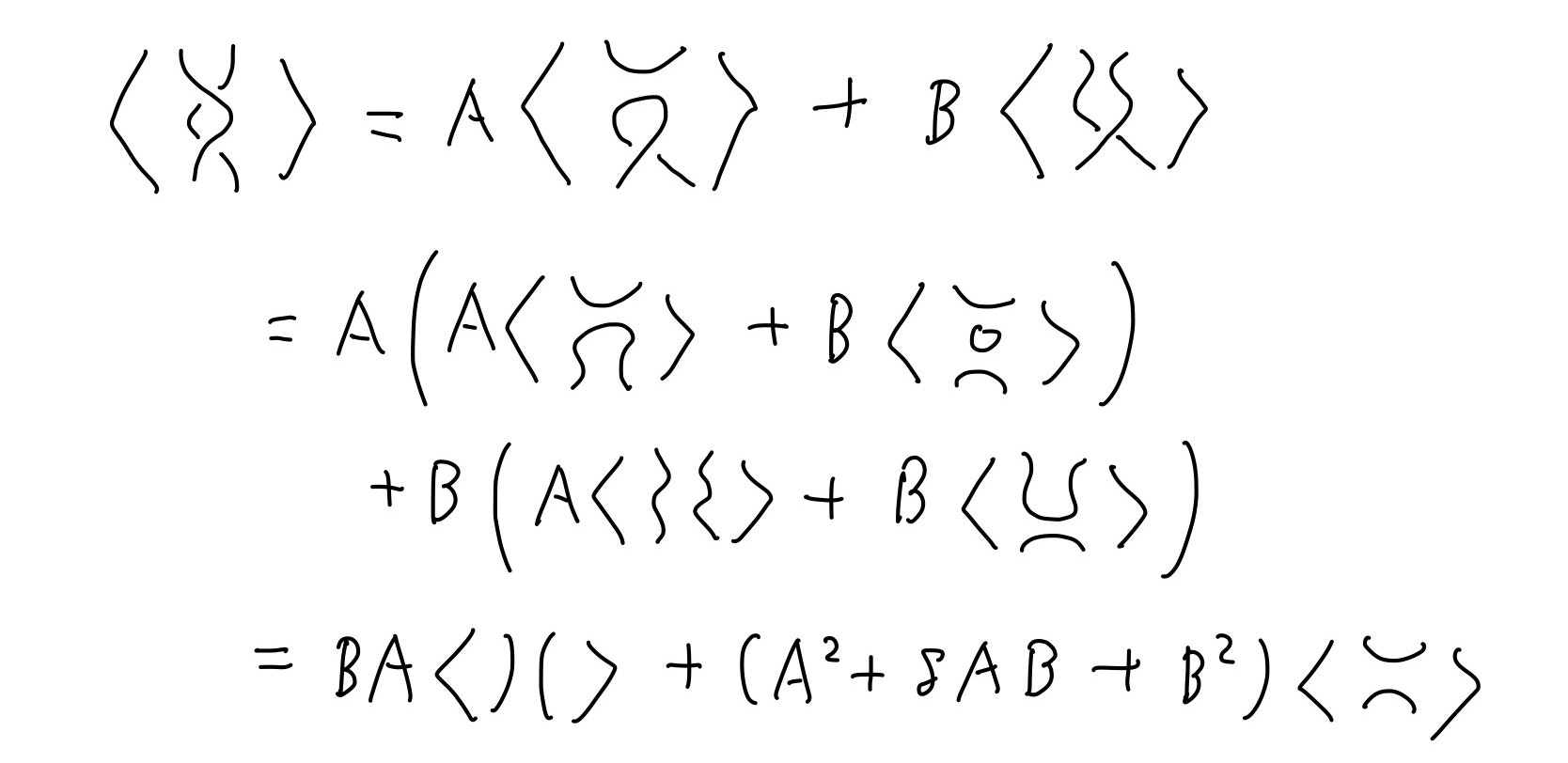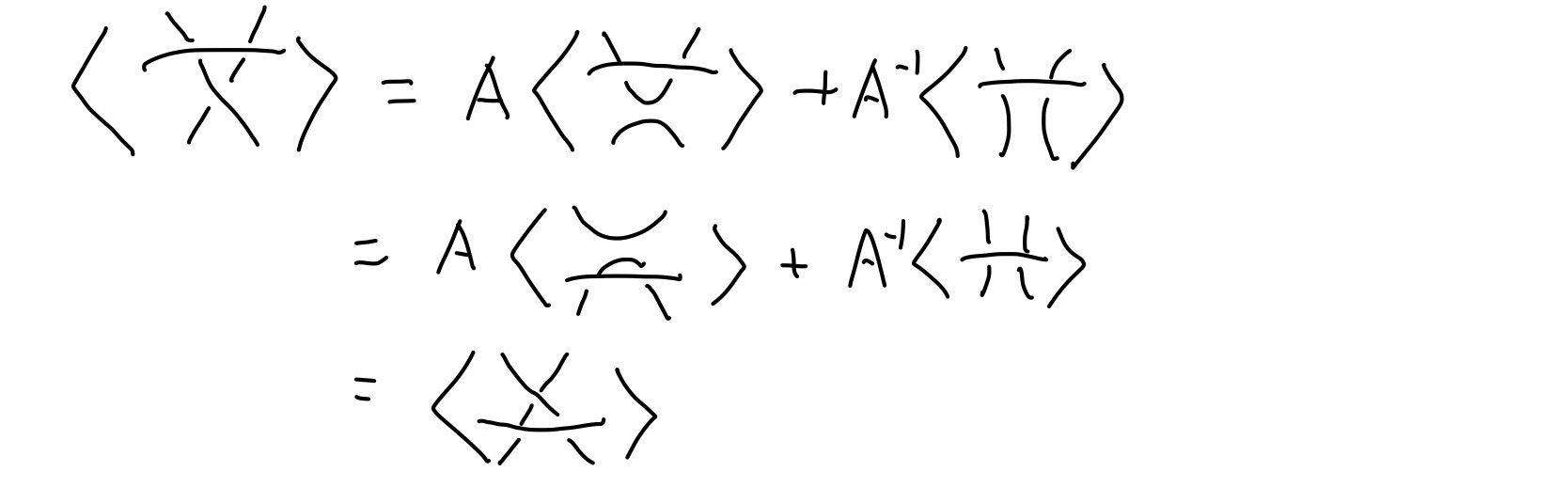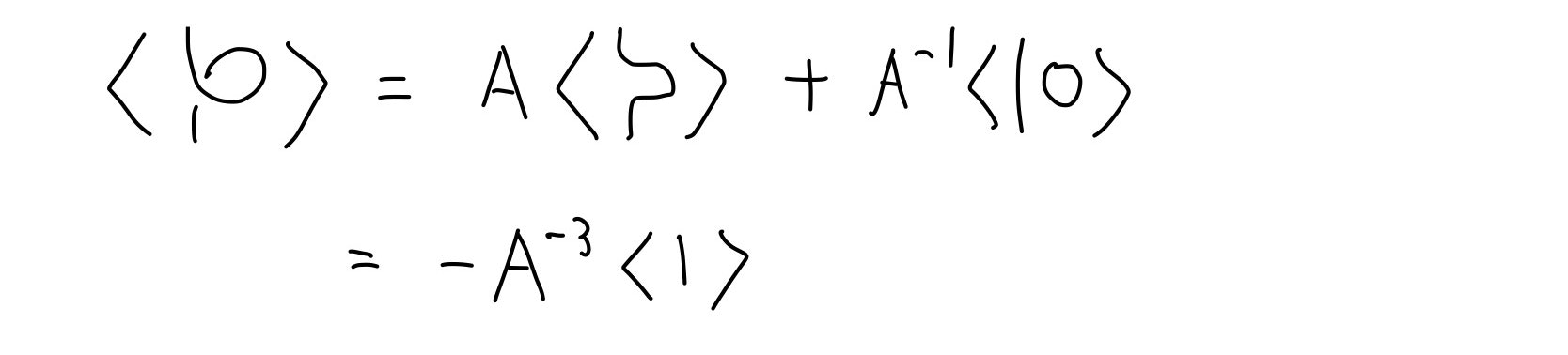手が悴んでパソコンに文字を入力することさえ辛くなるような寒い部屋で1人、やらなければならないことから逃げつつこの記事を書いているのは、一体誰でしょう?
そう、私です。どうも、理学部物理学科3年のてつです。
今回は、結び目、あるいは絡み目について話していきたいと思います。
絡み目理論入門
結び目と絡み目
一本の紐を想像してください。その紐の片方の端を持ち、グニャグニャした後、もう一方の端と繋げてできる図形が結び目です。紐が複数本ある場合は絡み目といいます。結び目には以下のようなものがあります。
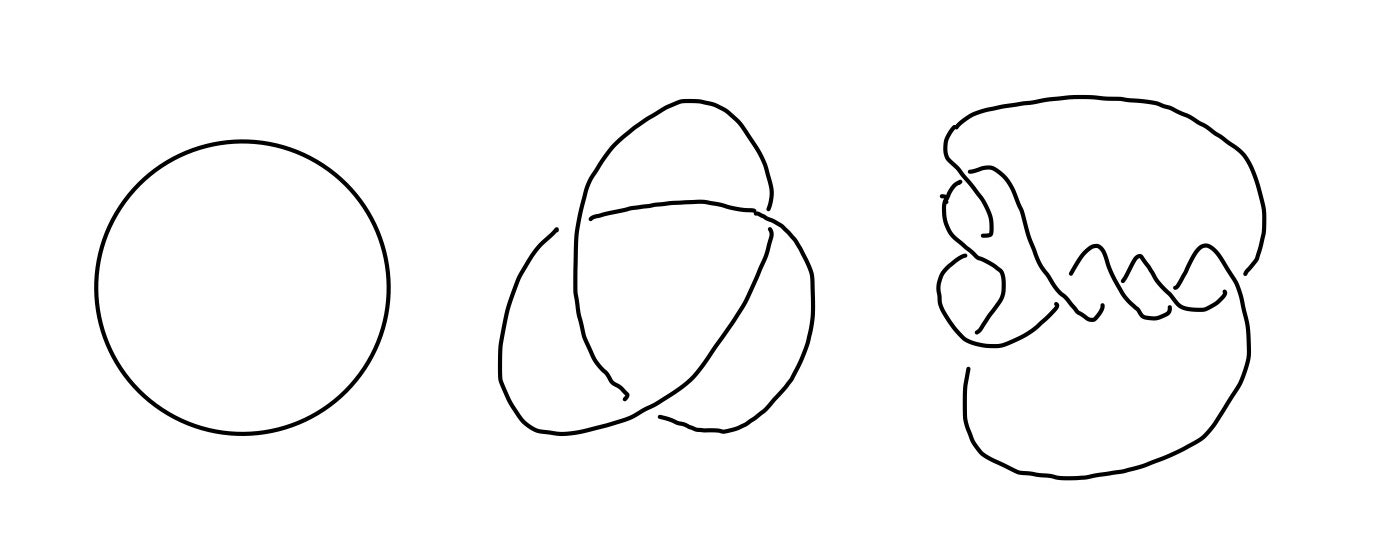
以下、絡み目、結び目という場合、それを平面に射影したものを表すこととします。
同値な絡み目
さて、ある絡み目を連続的に変形させて別の絡み目と同じ形にできるとき、この二つの絡み目は同じものとみなすことができ、このことを同値であるといいます。例えば、あやとりでできる図形は、変形するとあやとりの一番初めの状態、つまり円周になるので、これは円周と同値ということができるわけです。

これからやりたいことは、各絡み目に対し、連続的な変形で不変な量、つまり位相不変量を求めることです。絡み目に対する位相不変量を絡み目不変量といいます。これを求めることで、同値な絡み目は同じ絡み目不変量を持つことになり、絡み目をある程度分類することが可能になります。(ただし、異なる絡み目が必ず異なる不変量を持つわけではないので注意が必要です)。
ジョーンズ多項式
絡み目不変量にはさまざまなものがありますが、ここではそのうちの一つでよく知られている、ジョーンズ多項式について扱いたいと思います。
ライドマイスター操作
まず、絡み目における連続な変形がどのようなものかをみておきたいと思います。実は、絡み目での連続的な変形というのは、ライドマイスター操作という以下の3つの操作R(I)、R(II)、R(III)の有限回の組み合わせで表されることが知られています。
そのため、これからはこの3つの操作で不変な量を求めれば良いということになります。
カウフマンブラケット
突然ですが、ここである絡み目$U$に対し、カウフマンブラケット$\langle U \rangle$と呼ばれる多項式を以下のように再帰的に定義します。
- $U$にある交点の数が0個のとき、$U$に現れる円周の数を$r$として、$$\langle U \rangle = \delta^{r}$$
- $U$にある交点の数が$n$個のとき、$$\langle{U}\rangle = A\langle{U_{0}}\rangle+B\langle{U_\infty}\rangle$$
ただし、$U_0$と$U_\infty$とは、$U$に現れる交点の1つを下のように変形してできる絡み目とします。
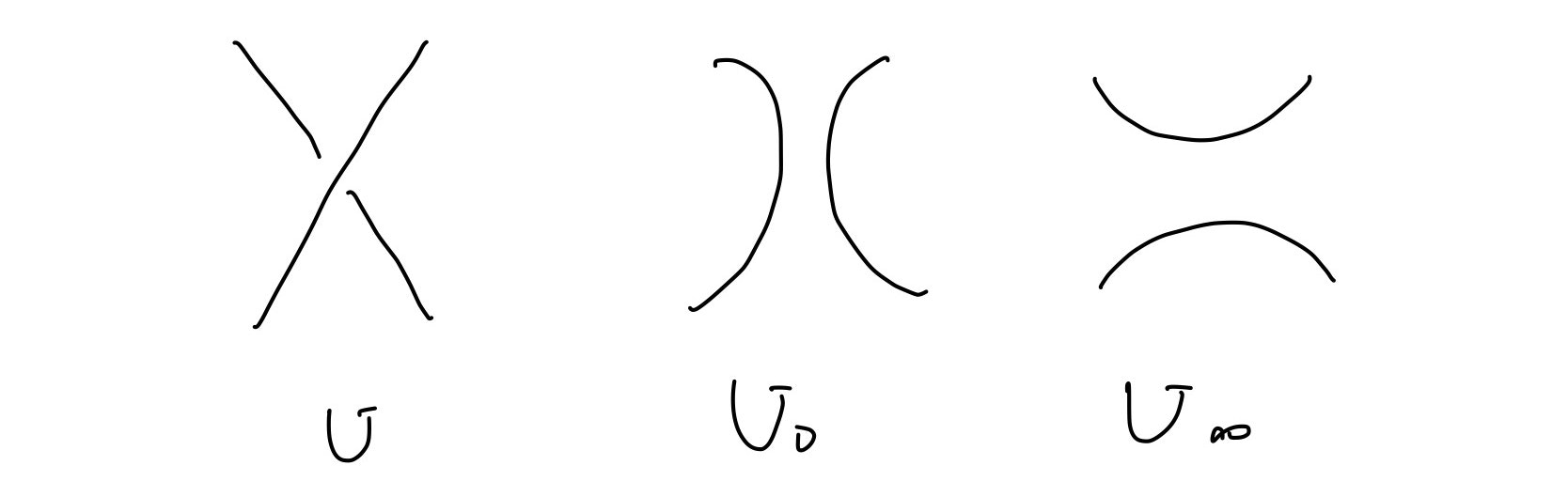
例
簡単な例として、$U$を下の図のような絡み目とした場合のカウフマンブラケットを求めてみましょう。

図形をパソコンで打ち込むことは困難なので手書きで書きますが、カウフマンブラケットは以下のように変形することができます。
よって、$$U = A^2\delta^2 +2AB\delta + B^2\delta^2$$
証明は略しますが、$\langle{U}\rangle$は、求める過程での交点の取り方にはよりません。
$U$を$U_0$あるいは$U_\infty$に置き換える操作を繰り返すと、交点の数はどんどん減っていきます。最終的には交点が0個になりますが、こうして得られる絡み目をステイトといいます。$\langle{U}\rangle$は、$U$からあるステイト$s$までに$U_0$への置換を$p$回、$U_\infty$への置換を$q$回施したとすると、$$\langle{U}\rangle = \sum_{s}A^pB^q\delta^{r(s)}$$と表せます。ただし、$r(s)$は$s$に出てくる円周の数、和はすべてのステイトに関する和です($s$への変形の結果が同じでも変形の仕方が違えば違うステイトとして数えます)。このことは先ほどの例をみるとよく理解できると思います。
R(II)に対する不変性
カウフマンブラケットは$A$、$B$、$\delta$についての多項式になっているわけですが、これは残念ながらライドマイスター操作に対して不変ではありません。これから不変にするためにはどうすればいいかを見ていきたいと思います。
まずはR(II)に対して不変にするにはどうすればいいかを考えたいと思います。以下の関係に注目しましょう。
この関係から、R(II)に対して不変な多項式にするための必要十分条件は$BA = AB = 1$、$A^2+\delta AB + B^2 = 0$であるとわかります。よって、$$B = A^{-1}$$ $$\delta = -(A^2+A^{-2})$$
このとき、R(III)に対して不変であることが以下のように示せます。途中の変形でR(II)への不変性を使っています。
さて、残るはR(I)だけです。しかし、以下のようにR(I)に対しては不変ではありません。
余分にかかった$-A^{-3}$をどうにかしなくてはなりません。そのために、新たな概念を導入します。
ねじれ数
R(I)を行うと、これまで求めてきた多項式には$-A^{-3}$がかかり、絡み目自体では交点、あるいはねじれの数が減ります。よって、あらかじめ多項式を$-A^{-3}$で、ねじれの数に対応する分だけ割っておけばR(I)を不変にすることができそうです。
そこで、ねじれ数というものを導入します。今、仮想的に絡み目に向きをつけることを考えます。すると、交点には2通りの区別できないパターンが出てくることがわかります。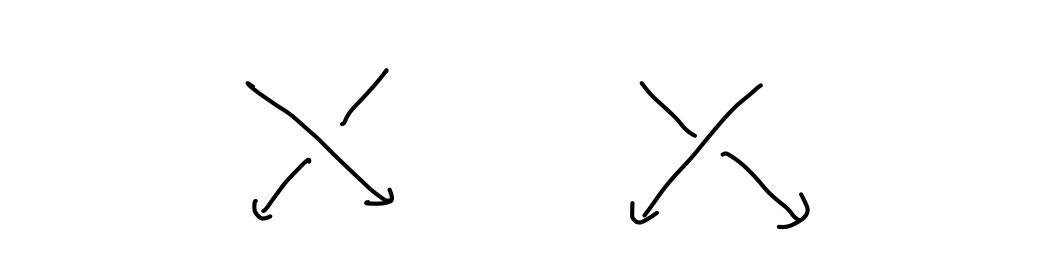
左側を$-1$の交点、右側を$+1$の交点と呼ぶことにします。いま、絡み目$U$に対して、$$w(U) = (+1\text{の交点の数})-(-1\text{の交点の数})$$のようにねじれ数を定義すると、ねじれ数を1増やす操作をすると$-A^{-3}$がかけられることから、$(-A^{-3})^{-w(U)}$を$\langle{U}\rangle$にかけておくとR(I)に対して不変になることがわかります。
ジョーンズ多項式
以上のようにして多項式$$V(U) = (-A^{-3})^{-w(U)}\langle{U}\rangle$$が定義されたわけです。この多項式は同値な多項式に対して不変で、この多項式をジョーンズ多項式といいます。
例
簡単な例を見てみましょう。下の図のような絡み目のジョーンズ多項式を考えます。

この絡み目のねじれ数は$-3$です。
また、ステイトは8つあり、した図のようになります。
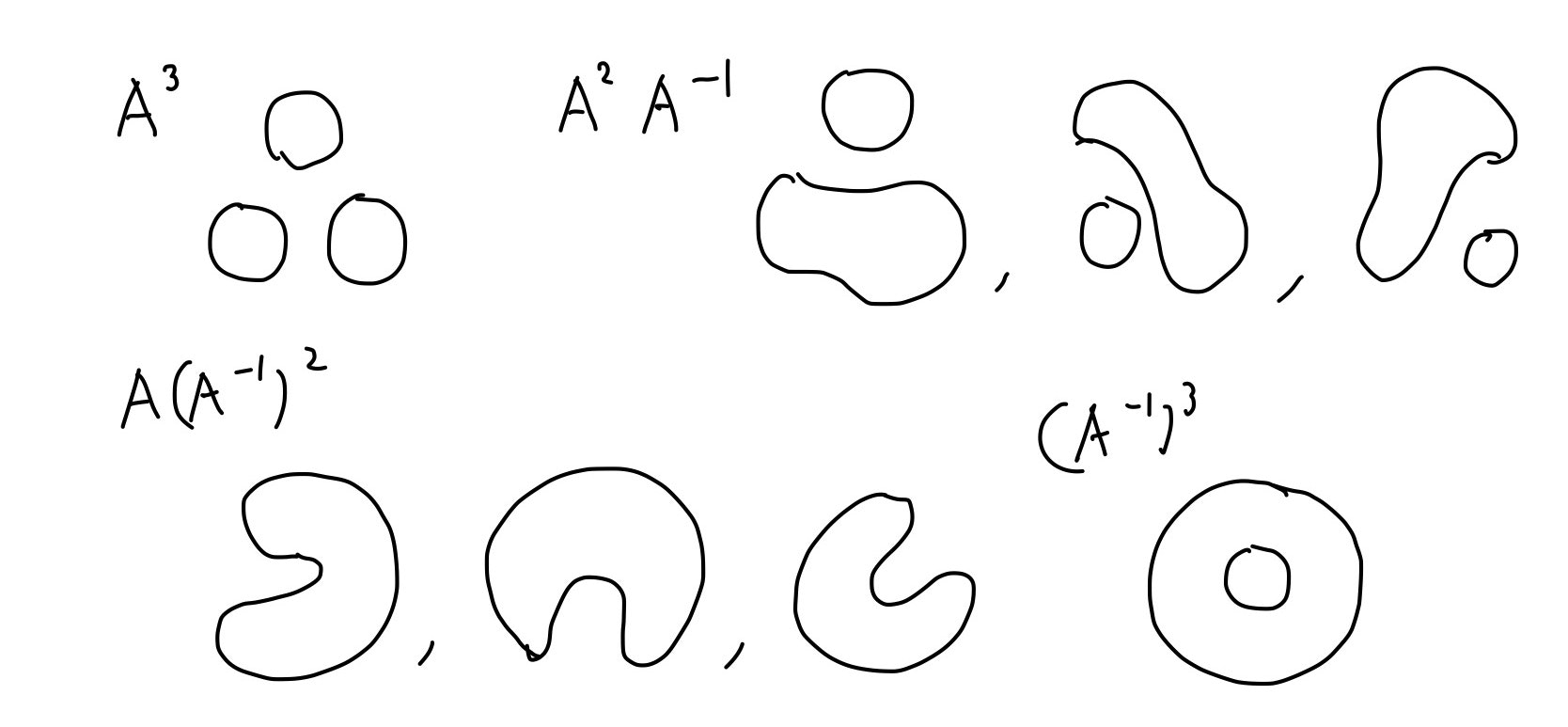
よって、このカウフマンブラケットは$$A^3\delta^3+A\delta^2+A^{-1}\delta + A^{-3}\delta^2 = -A^9-2A^5-A+A^{-3}+A^{-7}$$となります。
以上から、この絡み目のジョーンズ多項式は$$V(U) = A^{18}+2A^{14}-A^{10}+A^{6}+A^{2}$$
終わりに
いかがだったでしょうか。時間の関係もあってあまり深いところまで立ち入ることができなかったため、正直何が面白いのかわからなかった人も多いことでしょう。私としても残念です。絡み目とその多項式は、統計力学における可解模型の転送行列との関係や組み紐群の表現などさまざまな側面があります。今回はそこまで立ち入ることはできませんでしたが、またいつかもっと深い内容の記事が書けたらいいなと思います。
参考文献
- 伊藤昇 『結び目理論の圏論』 日本評論社(2018)
- 河内明夫 『レクチャー結び目理論』(現代数学の潮流) 共立叢書(2007)