はじめに
地図を見ても,そうは見えない件。
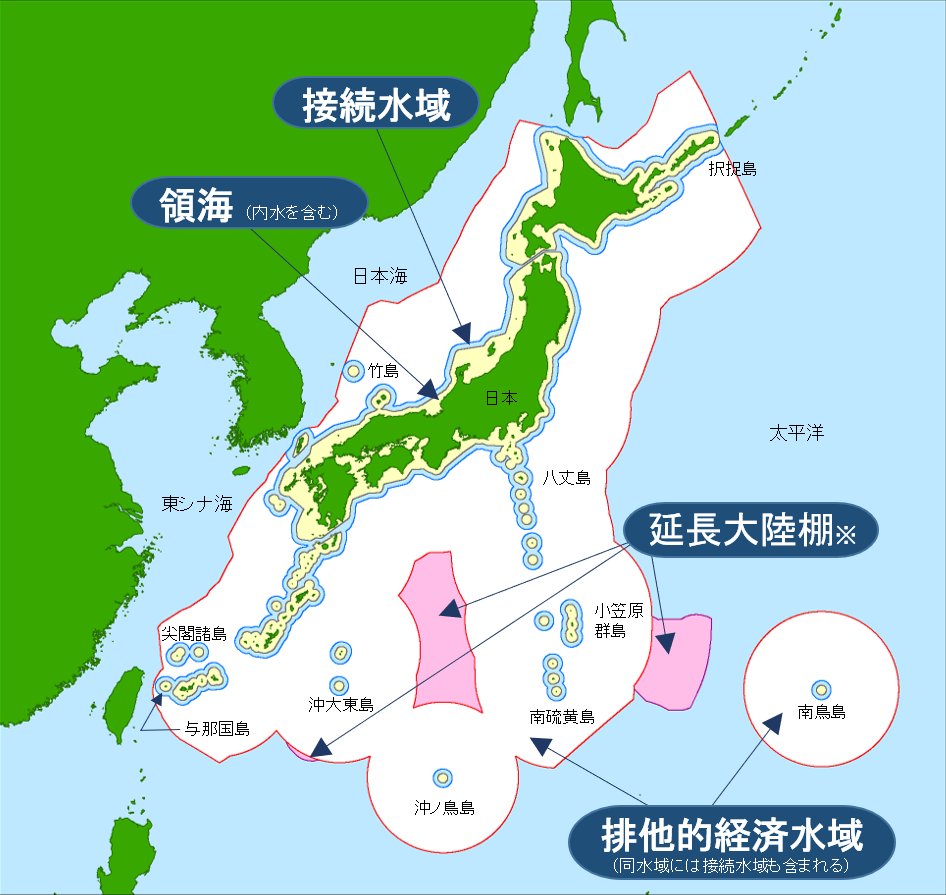
※本地図は海上保安庁ホームページ「日本の領海等概念図」より複製したもの。
試しに計算してみよう
まず,外務省の日本の領土をめぐる情勢によると,日本の領土面積は 38 万 8,000 平方キロメートルである。
次に沖ノ鳥島の排他的経済水域(Exclusive Economic Zone; EEZ)の面積を計算してみよう。排他的経済水域とは他国と競合しない限り,海岸(低潮時)から 200 海里の範囲のことをいう。簡単のため島の大きさを無視し,大東島や硫黄島の EEZ と少し重なっている部分も無視することにして,半径 200 海里の円の面積を求めよう。
一海里は 1,852 メートルであるから,
\begin{aligned}
\pi \times (200 \times 1852 \text{[m]})^2 &= 4.31 \times 10^{11} \ \text{[m²]} \\
&= 4.31 \times 10^5 \ \text{[km²]}
\end{aligned}
ということで 43 万 1,000 平方キロメートルとなった。つまり,沖ノ鳥島の EEZ が日本の領土面積より広いというのは本当らしい。
南硫黄島の EEZ の東南部が直線的なのは,サイパンなどの北マリアナ諸島(アメリカ自治領)の EEZ と接しているため。
目の錯覚か?
そもそも海上保安庁の地図では図法を明示していない。しかし,東経 115~160 度,北緯 15~50 度の範囲でメルカトル図法によって描いた地図とピタリ一致するので,おそらくメルカトル図法だと思われる。下記の地図をよく見ると,どんなに小さな島でも描いているように見える。ディスプレイが汚れている人は綺麗にして見てね。
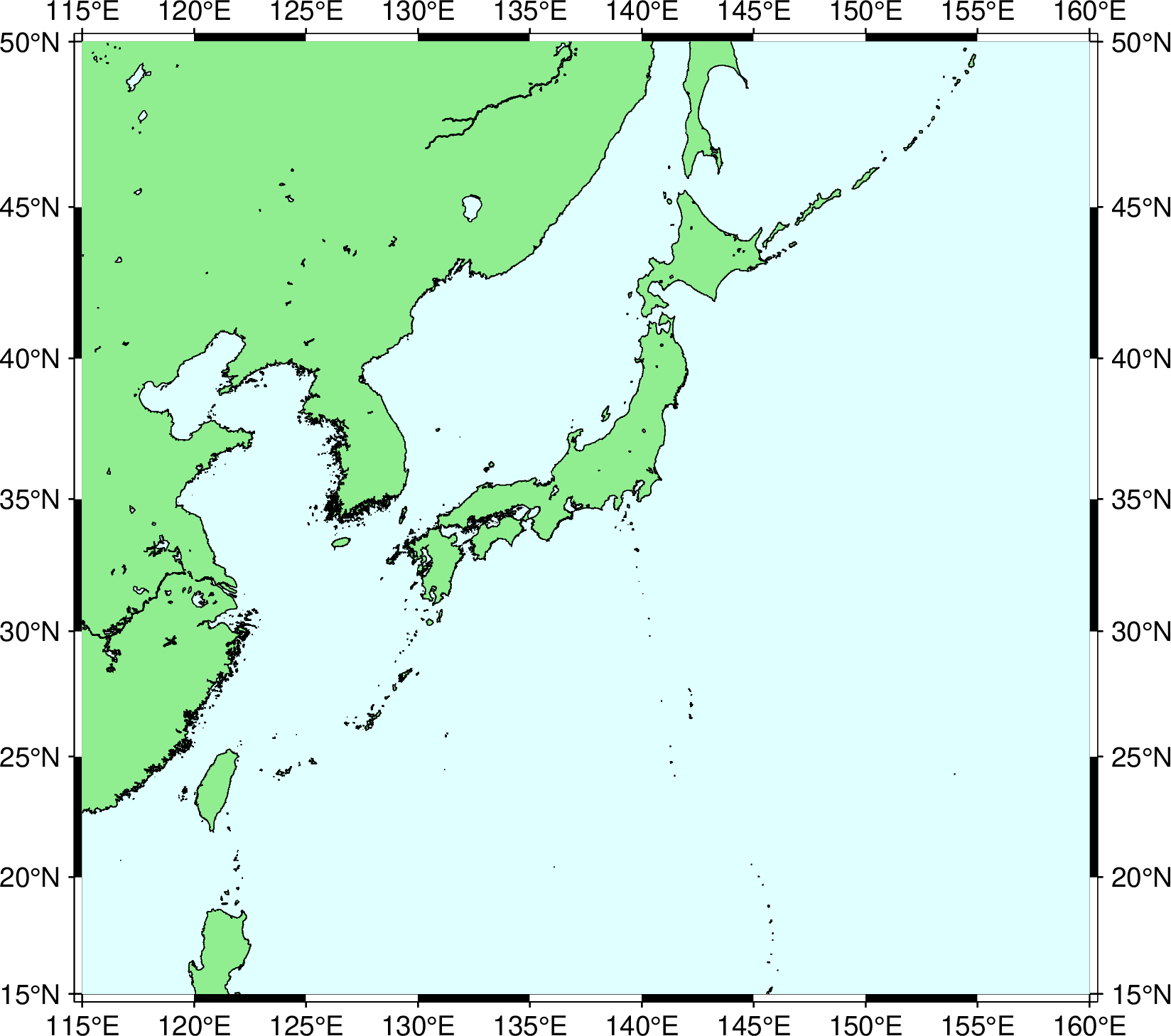
なお,上記の地図は GMT(Generic Mapping Tools)6.5.0 を用いて作図した。ちなみに GMT のスクリプト(バッチファイル)は下記のようになる。最終行の chcp 932 はコードページを元に戻すため。どうやら GMT のツール群はコードページを弄るようで,実行後に文字化けしてしまうのだ。
@echo off
gmt begin japan-eez png
gmt basemap -JM12c -R115/160/15/50 -Ba5f5 -BWSNE
gmt coast -Df -W0.25 -Slightcyan -Glightgreen
gmt end
chcp 932 > NUL
メルカトル図法の場合,緯度 $\phi$ とすると縦・横ともに $1/\cos\phi$ 倍ずつ拡大されるので,面積としては $1/\cos^2\phi$ 倍拡大され,高緯度地域は著しく大きく見えてしまう。
| 場所 | 緯度 $\phi$ | $1/\cos\phi$ | $1/\cos^2\phi$ |
|---|---|---|---|
| ①沖ノ鳥島 | 北緯20度25分 | 1.067 | 1.139 |
| ②東京都(都庁) | 北緯35度41分 | 1.231 | 1.516 |
| 比率(②/①) | 1.154 | 1.331 |
代表点として東京都(都庁)の緯度と比較してみても,面積としては $1.516/1.139 = 1.331$ 倍大きく見えていることになる。
こういう用途にメルカトル図法を使うのってどうなのよ?
GMT で EEZ の円を描く
先ほど GMT で描いた日本周辺地図に沖ノ鳥島を中心とした EEZ の円を描いてみよう。GMT には豊富なモジュールが用意されているとはいえ,参考文献を見る限り,一発で EEZ の円を描けるモジュールは無さそうなので,沖ノ鳥島(北緯 20 度 25 分,東経 136 度 04 分)を中心とした半径 200 海里(370.4km)の円周上の座標を求め,gmt plot モジュールを用いてそれらの座標を地図上にプロットしていく。
まず,北極点を中心とした EEZ 円を考える。簡単のため地球を完全球体とし,その半径を $R$ とおく。200 海里(370.4km)は直線距離ではなく,地表面上に沿った円弧の長さ $r$ とする。北極を中心とした EEZ 円周上の点と地球中心を結ぶ直線と Z 軸が結ぶ角度を $\varepsilon$ とおくと $r = R \varepsilon$ となる。これより北極点を中心とした EEZ 円周上の点の座標 $(x,y,z)$ は経度 $\delta$ とおくと北緯 $90 - \varepsilon$ 度点の集合なので
\left( \begin{matrix}
x \\ y \\ z
\end{matrix} \right) = \left( \begin{matrix}
R \sin \varepsilon \cos \delta \\
R \sin \varepsilon \sin \delta \\
R \cos \varepsilon
\end{matrix} \right) \tag{1}
と書ける。沖ノ鳥島の経度 $\alpha$,緯度 $\beta$ とおくと,これらの点を Y 軸を中心として $90 - \beta$ 度回転させた後,Z 軸を中心として $\alpha$ 度回転させれば良い。
Y 軸を中心として $90 - \beta$ 度だけ回転させた後の座標 $(x', y', z')$ とおくと
\begin{align}
\left( \begin{matrix}
x' \\ y' \\ z'
\end{matrix} \right) &= \left( \begin{matrix}
\cos(90-\beta) & 0 & \sin(90-\beta) \\
0 & 1 & 0 \\
-\sin(90-\beta) & 0 & \cos(90-\beta)
\end{matrix} \right) \left( \begin{matrix}
x \\ y \\ z
\end{matrix} \right) \\
&= \left( \begin{matrix}
\sin\beta & 0 & \cos\beta \\
0 & 1 & 0 \\
-\cos\beta & 0 & \sin\beta
\end{matrix} \right) \left( \begin{matrix}
x \\ y \\ z
\end{matrix} \right) \tag{2}
\end{align}
となる。さらに Z 軸を中心として $\alpha$ 度だけ回転させた後の座標 $(x'', y'', z'')$ とおくと
\left( \begin{matrix}
x'' \\ y'' \\ z''
\end{matrix} \right) = \left( \begin{matrix}
\cos\alpha & -\sin\alpha & 0 \\
\sin\alpha & \cos\alpha & 0 \\
0 & 0 & 1
\end{matrix} \right) \left( \begin{matrix}
x' \\ y' \\ z'
\end{matrix} \right) \tag{3}
となる。座標 $(x'',y'',z'')$ の緯度 $\phi$,経度 $\theta$ とおくと,
\left( \begin{matrix}
x'' \\ y'' \\ z''
\end{matrix} \right) = \left( \begin{matrix}
R \cos \phi \cos \theta \\
R \cos \phi \sin \theta \\
R \sin \phi
\end{matrix} \right) \tag{4}
となる。これより
\left\lbrace
\begin{aligned}
\phi &= \text{asin} \left( \frac{z''}{R} \right) \\
\theta &= \text{atan2} \left( \frac{x''}{R\cos\phi}, \frac{y''}{R\cos\phi} \right)
\end{aligned} \right. \tag{5}
となる。
こうして得られた沖ノ鳥島を中心とする EEZ 円の経度・緯度データを以下に示す。
経度・緯度データはコチラ
gmt plot モジュールの仕様に合わせて経度,緯度の順に並べている。$\delta$ は 1 度刻みで,360 点の座標を求めた。ちなみに計算には Microsoft Excel を用いた。
136.067 17.078
136.128 17.079
136.188 17.080
136.249 17.083
136.310 17.086
136.371 17.091
136.432 17.096
136.492 17.103
136.553 17.110
136.613 17.118
136.673 17.128
136.733 17.138
136.793 17.150
136.852 17.162
136.912 17.175
136.971 17.190
137.029 17.205
137.088 17.221
137.146 17.238
137.204 17.256
137.262 17.276
137.319 17.296
137.376 17.316
137.433 17.338
137.489 17.361
137.544 17.385
137.600 17.410
137.655 17.435
137.709 17.461
137.763 17.489
137.816 17.517
137.869 17.546
137.922 17.576
137.974 17.607
138.025 17.638
138.076 17.671
138.126 17.704
138.175 17.738
138.224 17.773
138.273 17.809
138.320 17.845
138.367 17.882
138.414 17.920
138.459 17.959
138.504 17.999
138.549 18.039
138.592 18.080
138.635 18.121
138.677 18.164
138.719 18.207
138.759 18.250
138.799 18.295
138.838 18.340
138.876 18.385
138.913 18.432
138.950 18.478
138.985 18.526
139.020 18.574
139.054 18.622
139.087 18.672
139.119 18.721
139.150 18.771
139.181 18.822
139.210 18.873
139.239 18.925
139.266 18.977
139.293 19.029
139.318 19.082
139.343 19.136
139.367 19.190
139.390 19.244
139.411 19.298
139.432 19.353
139.452 19.408
139.470 19.464
139.488 19.519
139.505 19.576
139.521 19.632
139.535 19.688
139.549 19.745
139.561 19.802
139.573 19.860
139.583 19.917
139.593 19.974
139.601 20.032
139.608 20.090
139.614 20.148
139.620 20.206
139.624 20.264
139.627 20.322
139.628 20.380
139.629 20.439
139.629 20.497
139.628 20.555
139.625 20.613
139.622 20.671
139.617 20.730
139.611 20.788
139.605 20.845
139.597 20.903
139.588 20.961
139.578 21.018
139.567 21.076
139.554 21.133
139.541 21.190
139.527 21.246
139.511 21.303
139.495 21.359
139.477 21.415
139.459 21.470
139.439 21.526
139.418 21.581
139.397 21.635
139.374 21.690
139.350 21.743
139.325 21.797
139.299 21.850
139.273 21.903
139.245 21.955
139.216 22.007
139.186 22.058
139.155 22.109
139.123 22.159
139.091 22.208
139.057 22.258
139.022 22.306
138.987 22.354
138.950 22.402
138.913 22.449
138.874 22.495
138.835 22.540
138.795 22.585
138.754 22.630
138.712 22.673
138.670 22.716
138.626 22.758
138.582 22.800
138.537 22.841
138.491 22.881
138.444 22.920
138.397 22.958
138.348 22.996
138.299 23.033
138.250 23.069
138.199 23.104
138.148 23.139
138.097 23.172
138.044 23.205
137.991 23.237
137.938 23.268
137.883 23.298
137.829 23.328
137.773 23.356
137.717 23.383
137.661 23.410
137.604 23.435
137.546 23.460
137.488 23.484
137.430 23.507
137.371 23.528
137.312 23.549
137.252 23.569
137.192 23.588
137.131 23.606
137.071 23.623
137.009 23.639
136.948 23.654
136.886 23.668
136.824 23.681
136.762 23.692
136.699 23.703
136.637 23.713
136.574 23.722
136.511 23.730
136.448 23.736
136.384 23.742
136.321 23.747
136.257 23.751
136.194 23.753
136.130 23.755
136.067 23.755
136.003 23.755
135.939 23.753
135.876 23.751
135.812 23.747
135.749 23.742
135.686 23.736
135.622 23.730
135.559 23.722
135.497 23.713
135.434 23.703
135.371 23.692
135.309 23.681
135.247 23.668
135.185 23.654
135.124 23.639
135.063 23.623
135.002 23.606
134.942 23.588
134.881 23.569
134.822 23.549
134.762 23.528
134.703 23.507
134.645 23.484
134.587 23.460
134.530 23.435
134.473 23.410
134.416 23.383
134.360 23.356
134.305 23.328
134.250 23.298
134.196 23.268
134.142 23.237
134.089 23.205
134.037 23.172
133.985 23.139
133.934 23.104
133.884 23.069
133.834 23.033
133.785 22.996
133.737 22.958
133.689 22.920
133.643 22.881
133.597 22.841
133.552 22.800
133.507 22.758
133.464 22.716
133.421 22.673
133.379 22.630
133.338 22.585
133.298 22.540
133.259 22.495
133.221 22.449
133.183 22.402
133.147 22.354
133.111 22.306
133.076 22.258
133.043 22.208
133.010 22.159
132.978 22.109
132.947 22.058
132.917 22.007
132.889 21.955
132.861 21.903
132.834 21.850
132.808 21.797
132.783 21.743
132.759 21.690
132.737 21.635
132.715 21.581
132.694 21.526
132.675 21.470
132.656 21.415
132.638 21.359
132.622 21.303
132.607 21.246
132.592 21.190
132.579 21.133
132.567 21.076
132.556 21.018
132.546 20.961
132.537 20.903
132.529 20.845
132.522 20.788
132.516 20.730
132.512 20.671
132.508 20.613
132.506 20.555
132.504 20.497
132.504 20.439
132.505 20.380
132.507 20.322
132.510 20.264
132.514 20.206
132.519 20.148
132.525 20.090
132.532 20.032
132.541 19.974
132.550 19.917
132.561 19.860
132.572 19.802
132.585 19.745
132.598 19.688
132.613 19.632
132.628 19.576
132.645 19.519
132.663 19.464
132.682 19.408
132.701 19.353
132.722 19.298
132.744 19.244
132.767 19.190
132.790 19.136
132.815 19.082
132.841 19.029
132.867 18.977
132.895 18.925
132.923 18.873
132.953 18.822
132.983 18.771
133.014 18.721
133.046 18.672
133.079 18.622
133.113 18.574
133.148 18.526
133.184 18.478
133.220 18.432
133.257 18.385
133.296 18.340
133.335 18.295
133.374 18.250
133.415 18.207
133.456 18.164
133.498 18.121
133.541 18.080
133.585 18.039
133.629 17.999
133.674 17.959
133.720 17.920
133.766 17.882
133.813 17.845
133.861 17.809
133.909 17.773
133.958 17.738
134.007 17.704
134.058 17.671
134.108 17.638
134.160 17.607
134.212 17.576
134.264 17.546
134.317 17.517
134.370 17.489
134.424 17.461
134.479 17.435
134.534 17.410
134.589 17.385
134.645 17.361
134.701 17.338
134.757 17.316
134.814 17.296
134.871 17.276
134.929 17.256
134.987 17.238
135.045 17.221
135.104 17.205
135.163 17.190
135.222 17.175
135.281 17.162
135.341 17.150
135.400 17.138
135.460 17.128
135.520 17.118
135.581 17.110
135.641 17.103
135.702 17.096
135.762 17.091
135.823 17.086
135.884 17.083
135.945 17.080
136.006 17.079
GMT のスクリプト(バッチファイル)を以下に示す。
@echo off
gmt begin japan-eez2 png
gmt basemap -JM12c -R115/160/15/50 -Ba5f5 -BWSNE
gmt coast -Df -W0.25 -Slightcyan -Glightgreen
gmt plot -L -W0.25,Red eez-circle.txt
gmt end
chcp 932 > NUL
沖ノ鳥島を中心とした EEZ 円を描き加えた地図を以下に示す。海上保安庁の地図を再現したに過ぎないので,赤い円の内部面積が日本領土面積よりも広いようには見えないのは当たり前だ。

正積図法で描く
さて,ここからが本番である。メルカトル図法のような高緯度地域の面積が拡大される図法ではなく,正積図法を使って日本周辺地図および沖ノ鳥島を中心とした EEZ 円を描いてみよう。
GMT のスクリプト(バッチファイル)を以下に示す。
@echo off
gmt begin japan-eez3 png
gmt basemap -JB135/35/30/45/12c -R115/155/15/50 -BWSNE -Ba5f5
gmt coast -W0.25 -Df -Slightcyan -Glightgreen
gmt plot -L -W0.25,Red eez-circle.txt
gmt end
chcp 932 > NUL
アルベルス正積円錐図法による日本周辺地図を以下に示す。EEZ 円が歪んで横長に見える。
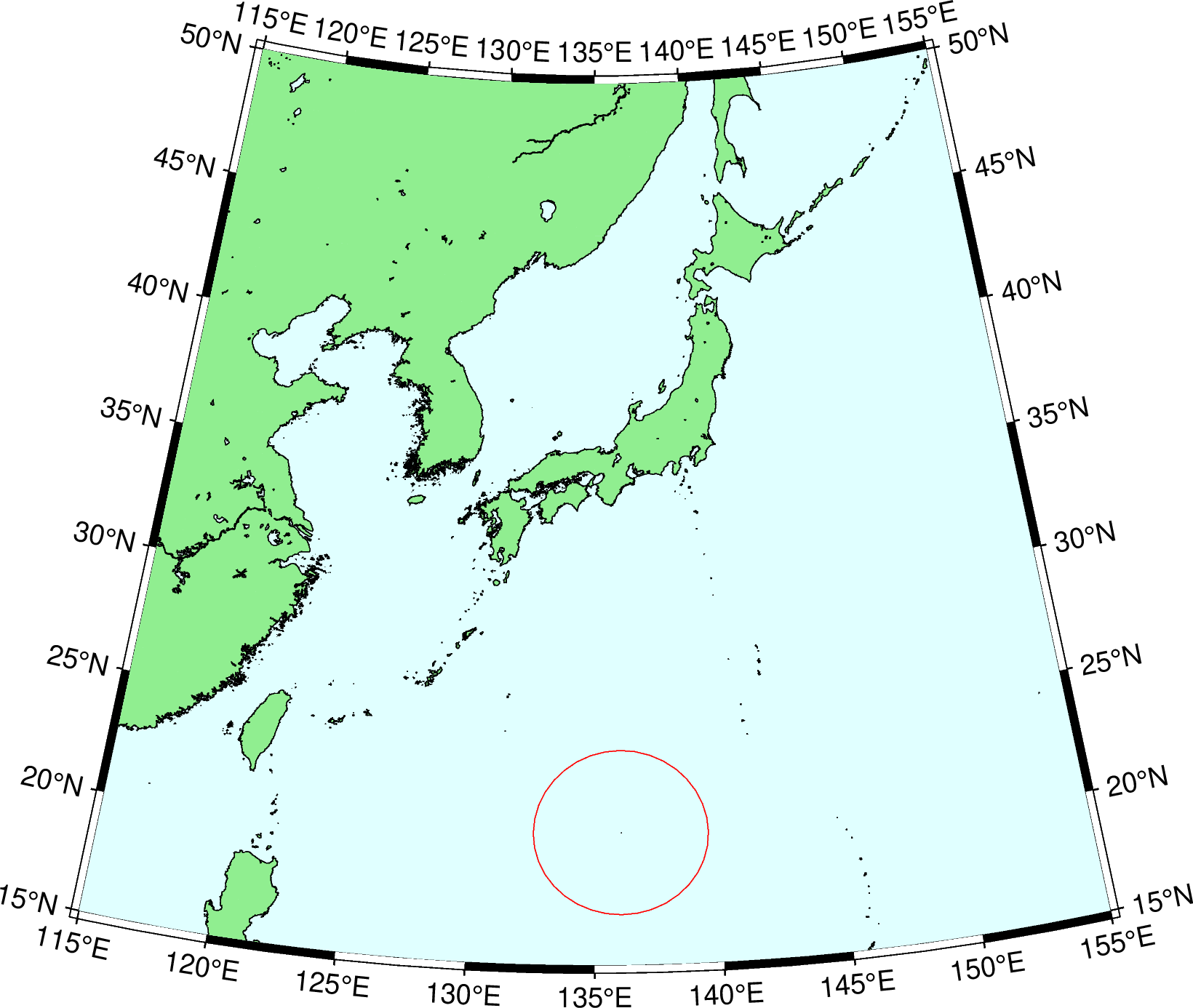
あれれ?これでも赤い円が日本領土面積よりも広いようには見えない・・・
面積を測ってみよう
仕方ないので面積を計測してみる。GMT スクリプト(バッチファイル)は下記の通り。今回は湖沼部も黒く塗り潰す。できるだけ高精細にするため先ほどの地図の 10 倍の解像度とした。このため生成された画像ファイルは 14244×12642 ピクセルにもなる。
@echo off
gmt begin japan-eez4a png
gmt basemap -JB135/35/30/45/120c -R115/155/15/50 -Bf5
gmt coast -W0.25 -Df -Gblack -Cblack
gmt end
gmt begin japan-eez4b png
gmt basemap -JB135/35/30/45/120c -R115/155/15/50 -Bf5
gmt plot -L -W0.25,black -Gblack eez-circle.txt
gmt end
chcp 932 > nul
こうして作成した画像ファイルから手作業で地図の枠や他国の領土を注意深く取り除く。うっかり竹島や尖閣諸島を削除したら各方面からお𠮟りを受けるので細心の注意を払って作業する。
しかし,表1を見ても右の円のほうが面積が広いと思えるだろうか?
 japan-eez4a.png(修正後) |
 japan-eez4b.png(修正後) |
|---|
以下は突貫で作った黒いピクセル数をカウントする C# プログラムである。GetPixel メソッドはクッソ遅いが,このプログラムは今回しか使わないので我慢する。とはいえ数分程度で終わるとは思う。
using System;
using System.IO;
using System.Drawing;
class PixelCount {
static int Main( string[] args ) {
if( args.Length < 1 ) {
Console.Error.WriteLine( "Usage: PixelCount(.exe) [画像ファイル名]" );
return -1;
}
if( !File.Exists( args[0] ) ) {
Console.Error.WriteLine( "ファイル {0} は存在しません!!", args[0] );
return -1;
}
Bitmap bitmap = new Bitmap( args[0] );
double count = 0;
for( int y = 0; y < bitmap.Height; y++ ) {
for( int x = 0; x < bitmap.Width; x++ ) {
var color = bitmap.GetPixel( x, y );
int value = color.G + color.B + color.R;
count += 3 * 255 - value;
}
}
Console.WriteLine( (double)count / ( 3 * 255 ) );
return 0;
}
}
上記のプログラムの実行結果を示す。
| 画像ファイル名 | 面積(ピクセル) | |
|---|---|---|
| 日本領土 | japan-eez4a.png | 3,818,414 |
| 沖ノ鳥島中心の EEZ 円 | japan-eez4b.png | 4,268,957 |
をををを!やっぱり沖ノ鳥島中心の EEZ 円のほうが日本領土より広かったのだ。しかも,その比率を求めてみると
\frac{4,268,957\,\text{[px]}}{3,818,414\,\text{[px]}} = 1.12
となり,実際の面積比
\frac{431,000\,\text{[km²]}}{388,000\,\text{[km²]}} = 1.11
に極めて近しいことが分かる。
やはり,目の錯覚だったようだ・・・
備考
日本の領土面積は干潮時の海岸線を元にして計算されていると思うが,gmt coast モジュールの描く海岸線は干潮・満潮どちらの条件なのだろうか?調べても分からなかった。
補足
あまりにも遅かったので面積計測プログラムを高速化した。
参考文献
-
日本の領海等概念図 - 海上保安庁
本記事で引用した地図である(2024 年 10 月 25 日参照)。海上保安庁の場合,出典を明示すれば自由に引用・複製可能なのは嬉しい。 -
排他的経済水域(EEZ)とは?可能性を秘めた日本の海を知ろう - 東京都
東京都は海上保安庁の地図を引用。東京都の場合,知的財産権の規定が厳しいので要注意。リンクは OK だが,複製は禁止である。 -
海上保安体制強化に関する方針について - 首相官邸

この地図は東経 165 度線および北緯 17 度線がまっすぐ引かれていることから何らかの円筒図法を用いて作図したと思われるが,メルカトル図法でもなく正距円筒図法でもなくランベルト正積円筒図法でもないようだ。GMT で作成したいずれの図法の地図とも重ならなかった。図法が不明なことから本記事の題材にすることを断念した。 -
日本の排他的経済水域 - wikipedia
wikipedia の地図は首相官邸ホームページ掲載資料より抽出したもの。 -
日本の東西南北端の位置図 - 国土地理院
さすがに首相官邸ホームページに掲載する資料に GMT のような海外製のフリーソフトウェアを使うのは避けたかったのかもしれない。ならば国土地理院作成の地図を使ったのではないかと推察した。国土地理院の「500万分1 日本とその周辺」地図と似ているように見えるが,残念ながら重ならない。 -
Q3.16:国土地理院で刊行している地図は,どのような図法を使用していますか? - 国土地理院
「500万分1日本と周辺」地図は東京を投影中心とした正距方位図法とのこと。 -
はじめてのGMT6(グラフ編) - 6からはじめるGMT はじめよう!GMT6
このサイトの情報は非常に有用だが「EU加盟国からのアクセスをお断りします」のため,EU加盟国からアクセスしている方は注意されたい。